 |
Главная |
Краткие теоретические сведения. В практике обработки экспериментальных данных могут быть ситуации
|
из
5.00
|
В практике обработки экспериментальных данных могут быть ситуации, когда применение лагранжевой аппроксимации (например, полиномиальной) не оправдано или в принципе невозможно.
Примером такой ситуации могут служить случаи, когда набор экспериментальных данных был получен со значительной погрешностью, либо на измеряемую (зависимую) величину влияли некоторые дополнительные, не учитываемые факторы. Для демонстрации этой ситуации на левом рисунке представлены экспериментальные точки, истинная неизвестная кривая f(x) и аппроксимирующая кривая  (x), полученная одним из методов лагранжевой аппроксимации.
(x), полученная одним из методов лагранжевой аппроксимации.
 . .
|
На рисунке представлена ситуация, когда экспериментальные замеры в каждом узле проводились неоднократно и, вследствие указанных выше причин, дали разные результаты. В этом случае применение лагранжевой аппроксимации в принципе невозможно, так как каждому узлу  соответствует несколько разных значений
соответствует несколько разных значений 
В этих условиях требуется проводить аппроксимирующую кривую, которая не обязательно проходит через узловые точки, но в то же время отражает исследуемую зависимость и сглаживает возможные выбросы, возникшие из-за погрешности эксперимента.
Считаем известными значения экспериментальных данных в узлах  и через
и через  (x) обозначим непрерывную аппроксимирующую функцию. В узлах значения функций
(x) обозначим непрерывную аппроксимирующую функцию. В узлах значения функций  и
и  будут отличаться на величину
будут отличаться на величину  . Отклонения
. Отклонения  могут принимать как положительные, так и отрицательные значения. Чтобы не учитывать знаки, возведем каждое отклонение в квадрат, а для оценки близости функций
могут принимать как положительные, так и отрицательные значения. Чтобы не учитывать знаки, возведем каждое отклонение в квадрат, а для оценки близости функций  (x) и f(x) возьмем сумму этих квадратов
(x) и f(x) возьмем сумму этих квадратов

| (4.11) |
Метод построения аппроксимирующей функции  (x) из условия минимума величины Q называется методом наименьших квадратов ( далее - МНК).
(x) из условия минимума величины Q называется методом наименьших квадратов ( далее - МНК).
Наиболее распространен способ выбора функции  (x) в виде линейной комбинации
(x) в виде линейной комбинации  , где
, где  ,
,  , …,
, …,  - базисные функции;
- базисные функции;  ; с0,с1,…,сm - коэффициенты, определяемые при минимизации величины Q. Величину Q можно рассматривать как функцию нескольких переменных с0,с1,…,сm, т.е. Q= Q(с0,с1,…,сm). Минимум такой функции, как известно, достигается при равенстве нулю всех частных производных
; с0,с1,…,сm - коэффициенты, определяемые при минимизации величины Q. Величину Q можно рассматривать как функцию нескольких переменных с0,с1,…,сm, т.е. Q= Q(с0,с1,…,сm). Минимум такой функции, как известно, достигается при равенстве нулю всех частных производных  , i=0,1,2,…,m:
, i=0,1,2,…,m:

| |

| |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |

|
Путем несложных математических выкладок эту систему уравнений можно преобразовать к виду:

| (*) |

| |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |

|
где  ,
,  - скалярные произведения функций:
- скалярные произведения функций:
 ,
,  .
.
Выбор конкретных базисных функций зависит от свойств аппроксимируемой функцииf(x), таких, как периодичность, экспоненциальный или логарифмический характер, симметричность, наличие асимптот и т.д.
Здесь рассмотрим частный случай, когда аппроксимирующая функция имеет вид наклонной прямой линии  . Такую функцию можно представить как линейную комбинацию двух базисных функций
. Такую функцию можно представить как линейную комбинацию двух базисных функций  (x)=A
(x)=A  0(x)+B
0(x)+B  1(x), где
1(x), где  ,
,  .
.
Решение системы (*), расписанной для коэффициентов А и В имеет вид:
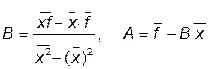 ,
,
где символ "надчеркивание" обозначает среднее значение:  , т.е.
, т.е.

| - среднее значение узловых точек аппроксимации; |

| - средний квадрат значений узловых точек аппроксимации; |

| - среднее значение аппроксимируемой функции в узловых точках; |

| - среднее произведений значений аппроксимируемой функции в узловых точках на значения соответствующих узловых точек. |
Если требуется построить аппроксимирующую функцию, имеющую нелинейный характер относительно независимой переменной x, то иногда удается перейти к линейной зависимости.
Например, пусть требуется найти аппроксимирующую функцию в виде  .
.
Прологарифмируем значения аппроксимируемой функции f (x) в узловых точках:  , i=0,1,2,…,n и для реализации
, i=0,1,2,…,n и для реализации  найдем линейную аппроксимирующую функцию
найдем линейную аппроксимирующую функцию  . Формулы для
. Формулы для  и
и  в этом случае выглядят так:
в этом случае выглядят так:
 ,
,
где  - среднее значение логарифмов аппроксимируемой функции в узловых точках.
- среднее значение логарифмов аппроксимируемой функции в узловых точках.
Чтобы теперь осуществить переход от функции  к функции
к функции  , надо пропотенцировать обе части равенства
, надо пропотенцировать обе части равенства  :
:

Величину  обозначим
обозначим  , а коэффициенты С и D, входящие в (4.21), вычисляются по формулам:
, а коэффициенты С и D, входящие в (4.21), вычисляются по формулам:
 .
.
Следовательно, последовательность действий при аппроксимации экспоненциальной зависимостью  выглядит так:
выглядит так:
1) вычисление логарифмов значений аппроксимируемой функции  ;
;
2) вычисление коэффициентов  и
и  ;
;
3) вычисление коэффициентов С и D;
4) вычисление значений функции  при необходимых значениях х.
при необходимых значениях х.
Задание
Изучить теоретический материал: метод наименьших квадратов.
По имеющемуся набору экспериментальных данных о зависимости F(x) построить методом наименьших квадратов аппроксимирующую зависимость H(x) в виде H(x)=CeDx. Построить диаграмму с графиком функции H(x) на интервале аппроксимации в виде непрерывной линии и значениями аппроксимируемой функции F(x) в узловых точках.
Для защиты контрольной работы представить на компьютере EXCEL-файл решения задачи и рукописный отчет. В отчете по задаче 3 представить:
- полную запись найденной функции H(x);
- ответы на контрольные вопросы.
Пример решения задачи
A1’Аппроксимация зависимостей методом наименьших квадратов
A2’Исходные данные Объединить клетки A2,B2.
C2’Экспоненциальная зависимость Объединить клетки C2:F2, центрировать по горизонтали.
A3’x B3’F(x) C3’x*x D3’lnF E3’X*lnF F3’H(x)
Вводим исходные данные из таблицы индивидуальных заданий: в клетки A4:A23 - данные по x , в B4:B23 - по F(x)
Найдем средние значения необходимых величин:
A24’Средние Объединить клетки A24:E24, центрировать по горизонтали.
A25=СРЗНАЧ(A4:A23) Копируем A25 в С25:Е25.
Вычислим коэффициенты экспоненциальной модели C и D:
D26’C= D27’D= Прижать к правому краю.
E26=EXP(D25-E27*A25) E27=(A25*D25-E25)/(A25*A25-C25)
Построим графики аппроксимируемой и аппроксимирующей зависимостей:
Выделим диапазон A3:B23 и при нажатой клавише Ctrl диапазон F3:F23.
Далее – Вставка→Диаграммы→Точечная→гладкая линия
Встать мышкой на график F(x), нажать на правую кнопку мышки, выбрать «Изменить тип диаграммы → отдельные точки.
Полученная в результате описанных действий электронная таблица представлена ниже.
| A | B | C | D | E | F | |
| Аппроксимация зависимостей методом наименьших квадратов | ||||||
| Исходные данные | Экспоненциальная зависимость | |||||
| x | F(x) | x*x | ln F | x lnF | H(x) | |
| 2,4962 | 0,91477 | 0,91477 | 2,891491 | |||
| 2,7777 | 1,021623 | 1,021623 | 2,891491 | |||
| 3,2303 | 1,172575 | 1,172575 | 2,891491 | |||
| 1,4 | 3,6873 | 1,96 | 1,304894 | 1,826852 | 3,225252 | |
| 1,8 | 3,1263 | 3,24 | 1,13985 | 2,05173 | 3,597539 | |
| 1,8 | 4,0496 | 3,24 | 1,398618 | 2,517513 | 3,597539 | |
| 2,2 | 4,0617 | 4,84 | 1,401602 | 3,083524 | 4,012798 | |
| 2,2 | 4,187 | 4,84 | 1,431984 | 3,150366 | 4,012798 | |
| 2,6 | 4,5722 | 6,76 | 1,519994 | 3,951986 | 4,47599 | |
| 4,6821 | 1,543747 | 4,63124 | 4,992648 | |||
| 3,4 | 5,098 | 11,56 | 1,628848 | 5,538084 | 5,568943 | |
| 3,4 | 5,294 | 11,56 | 1,666574 | 5,666352 | 5,568943 | |
| 3,4 | 5,314 | 11,56 | 1,670345 | 5,679172 | 5,568943 | |
| 3,8 | 6,802 | 14,44 | 1,917217 | 7,285423 | 6,211759 | |
| 3,8 | 5,9254 | 14,44 | 1,779248 | 6,761143 | 6,211759 | |
| 4,2 | 7,1601 | 17,64 | 1,968524 | 8,267801 | 6,928774 | |
| 4,2 | 7,3484 | 17,64 | 1,994483 | 8,376827 | 6,928774 | |
| 4,2 | 6,9879 | 17,64 | 1,94418 | 8,165556 | 6,928774 | |
| 4,6 | 7,4138 | 21,16 | 2,003343 | 9,215378 | 7,728553 | |
| 8,9416 | 2,190715 | 10,95357 | 8,62065 | |||
| Средние | ||||||
| 2,9 | 9,976 | 1,580657 | 5,011574 | |||
| С= | 2,2005 | |||||
| D= | 0,2731 | |||||

|
В качестве результата получили:
Экспоненциальная аппроксимирующая функция имеет вид:
H(x) = 2,2005 e0,2731x
Таблица индивидуальных заданий
| x | З н а ч е н и я ф у н к ц и и F(x) | ||||||||
| Вар.0 | Вар.1 | Вар.2 | Вар.3 | Вар.4 | Вар.5 | Вар.6 | Вар.7 | Вар.8 | |
| 1,00 | 1,0763 | 1,2517 | 1,3230 | 0,6277 | 1,8814 | 0,9359 | 2,0271 | 3,1520 | 3,8376 |
| 1,00 | 1,0958 | 2,4367 | 1,4282 | 1,8690 | 1,8362 | 1,9856 | 2,3484 | 2,4568 | 3,9836 |
| 1,00 | 1,1383 | 1,1782 | 1,2831 | 0,4060 | 1,8883 | 2,3470 | 2,2181 | 3,4022 | 3,8886 |
| 1,40 | 1,0164 | 1,3449 | 1,1846 | 1,3298 | 1,4621 | 1,9700 | 1,8576 | 3,7402 | 3,0142 |
| 1,80 | 0,8448 | 0,8970 | 1,0423 | 2,2396 | 1,2024 | 1,5461 | 1,2000 | 3,0803 | 2,2973 |
| 1,80 | 0,8451 | 2,2131 | 0,9386 | 2,0336 | 1,1520 | 2,7466 | 1,4444 | 4,0553 | 2,2882 |
| 2,20 | 0,7522 | 1,3838 | 0,8643 | 1,4532 | 1,2381 | 2,6644 | 0,8736 | 4,2548 | 1,6501 |
| 2,20 | 0,7373 | 2,9157 | 0,8048 | 2,8410 | 1,0669 | 2,1950 | 1,2159 | 3,0945 | 1,7271 |
| 2,60 | 0,7308 | 3,0485 | 0,6675 | 2,3196 | 0,7721 | 3,2191 | 0,9074 | 3,9021 | 1,3626 |
| 3,00 | 0,6000 | 2,9941 | 0,5978 | 3,7697 | 0,5254 | 4,5961 | 0,8578 | 5,3027 | 1,0164 |
| 3,40 | 0,4993 | 6,2228 | 0,5266 | 3,4957 | 0,4590 | 5,3854 | 0,4581 | 6,2270 | 0,7018 |
| 3,40 | 0,5338 | 4,2152 | 0,5803 | 4,0342 | 0,5279 | 5,3272 | 0,5526 | 5,2139 | 0,6705 |
| 3,40 | 0,5165 | 6,6556 | 0,4813 | 3,7366 | 0,7434 | 4,8497 | 0,5025 | 5,9395 | 0,7366 |
| 3,80 | 0,4420 | 6,2930 | 0,5195 | 4,5619 | 0,6277 | 4,7786 | 0,3066 | 6,4788 | 0,5702 |
| 3,80 | 0,4321 | 6,6981 | 0,5007 | 5,2506 | 0,6442 | 4,7873 | 0,3551 | 6,5435 | 0,5858 |
| 4,20 | 0,3882 | 9,4535 | 0,4187 | 5,7408 | 0,5844 | 6,5967 | 0,1355 | 7,2520 | 0,3684 |
| 4,20 | 0,4114 | 8,2133 | 0,4140 | 5,3274 | 0,5569 | 6,5855 | 0,4400 | 6,5925 | 0,4366 |
| 4,20 | 0,4066 | 8,4742 | 0,4621 | 5,6536 | 0,1952 | 6,7917 | 0,5134 | 6,7186 | 0,5113 |
| 4,60 | 0,3975 | 11,9610 | 0,2657 | 7,4624 | 0,3174 | 7,9354 | 0,2827 | 7,2521 | 0,2800 |
| 5,00 | 0,3139 | 15,6451 | 0,1904 | 8,9393 | 0,3803 | 9,8607 | 0,3911 | 9,5950 | 0,1901 |
| x | З н а ч е н и я ф у н к ц и и F(x) | ||||||||
| Вар.9 | Вар.10 | Вар.11 | Вар.12 | Вар.13 | Вар.14 | Вар.15 | Вар.16 | Вар.17 | |
| -1,00 | 1,2188 | 7,4220 | 0,8739 | 5,2215 | 0,7932 | 2,7183 | 0,9169 | 2,3129 | 0,6040 |
| -1,00 | 1,8744 | 7,2743 | 0,3451 | 5,2551 | 0,7023 | 2,7224 | 0,5457 | 2,2731 | 1,3795 |
| 0,10 | 2,5227 | 3,9034 | 0,2551 | 3,1721 | 0,6109 | 1,7278 | 0,4102 | 1,3882 | 0,5093 |
| 1,40 | 3,7513 | 1,9399 | 1,1792 | 1,8205 | 1,5195 | 1,4338 | 0,7612 | 0,8849 | 1,8638 |
| 1,80 | 3,2916 | 1,4080 | 2,7255 | 1,0110 | 1,1280 | 1,2160 | 2,6846 | 0,6750 | 2,8831 |
| 1,80 | 2,6521 | 1,4022 | 1,6945 | 1,4741 | 1,2064 | 0,8360 | 2,0052 | 0,9361 | 1,8943 |
| 1,90 | 3,7389 | 1,2177 | 1,7536 | 1,0859 | 2,0333 | 0,7749 | 2,0041 | 1,1275 | 3,0288 |
| 2,00 | 3,0509 | 1,2728 | 2,7337 | 1,1864 | 1,4756 | 0,6660 | 3,1356 | 0,7449 | 2,9470 |
| 2,00 | 3,7143 | 1,4258 | 2,1889 | 1,2272 | 1,9645 | 0,6387 | 2,4937 | 1,0536 | 3,1886 |
| 2,20 | 4,0200 | 1,3204 | 2,4792 | 1,0077 | 2,3354 | 0,7531 | 2,4977 | 1,0592 | 3,5239 |
| 2,40 | 3,7461 | 1,1501 | 2,5267 | 1,1415 | 3,0000 | 0,5561 | 3,1217 | 0,5687 | 3,8096 |
| 2,40 | 4,8381 | 1,0199 | 2,4428 | 1,1088 | 2,8193 | 0,5975 | 3,3006 | 0,7909 | 2,9615 |
| 3,00 | 5,0505 | 0,4076 | 4,3727 | 0,4204 | 2,9146 | 0,8344 | 4,9770 | 0,3891 | 4,4011 |
| 3,00 | 4,6304 | 0,4654 | 4,3626 | 0,7858 | 3,2616 | 0,6677 | 5,1370 | 0,6601 | 4,6679 |
| 3,30 | 5,9083 | 0,6565 | 4,7978 | 0,5386 | 3,3511 | 0,4719 | 7,2505 | 0,2628 | 4,3614 |
| 3,60 | 5,8075 | 0,3249 | 5,6142 | 0,6977 | 4,0366 | 0,5039 | 9,3677 | 0,3877 | 5,2419 |
| 3,60 | 5,8265 | 0,5175 | 5,6892 | 0,7369 | 3,7288 | 0,4352 | 8,9492 | 0,6351 | 5,0457 |
| 4,00 | 5,8601 | 0,1873 | 5,6279 | 0,1482 | 4,6823 | 0,1552 | 12,6004 | 0,5884 | 5,3645 |
| 4,00 | 7,3884 | 0,3377 | 5,3762 | 0,4855 | 5,5250 | 0,1569 | 12,9322 | 0,3862 | 6,3406 |
| 4,00 | 6,1544 | 0,2686 | 6,4613 | 0,2665 | 4,8807 | 0,5988 | 12,2746 | 0,3369 | 5,7087 |
| x | З н а ч е н и я ф у н к ц и и F(x) | ||||||||
| Вар.18 | Вар.19 | Вар.20 | Вар.21 | Вар.22 | Вар.23 | Вар.24 | Вар.25 | Вар.26 | |
| -2,00 | 10,5443 | 0,9998 | 10,2760 | 2,3529 | 1,3845 | 8,4827 | 4,2413 | 13,6799 | 1,9314 |
| -2,00 | 10,4500 | 0,8397 | 12,1079 | 2,1345 | 1,5908 | 8,7857 | 3,9753 | 14,1068 | 4,1296 |
| -2,00 | 10,5111 | 1,3915 | 11,4337 | 1,1536 | 1,8461 | 8,5152 | 2,7297 | 14,4267 | 4,1861 |
| -1,50 | 8,5483 | 3,1054 | 8,9798 | 3,8221 | 1,9248 | 6,1833 | 2,4454 | 10,8812 | 4,1504 |
| -0,50 | 4,7797 | 2,7413 | 6,4898 | 2,7490 | 2,5963 | 4,1893 | 3,2621 | 7,7228 | 6,9814 |
| -0,50 | 5,5932 | 3,7610 | 7,0710 | 4,7736 | 2,5332 | 3,6953 | 4,7954 | 8,3648 | 6,7332 |
| 0,00 | 4,0736 | 5,2426 | 5,2753 | 4,9639 | 2,8187 | 3,3739 | 4,5197 | 6,3934 | 5,6020 |
| 0,50 | 2,8870 | 5,6609 | 5,0244 | 5,3861 | 2,9823 | 2,6031 | 8,5462 | 4,8030 | 10,7851 |
| 0,50 | 2,8359 | 6,2277 | 4,9805 | 4,0506 | 3,3586 | 2,3200 | 7,2968 | 5,0912 | 7,1530 |
| 1,60 | 1,7123 | 7,7175 | 1,3983 | 7,2094 | 3,8109 | 1,5975 | 15,6168 | 3,2186 | 19,9620 |
| 1,60 | 2,1779 | 8,5510 | 1,8123 | 9,5566 | 3,8605 | 1,0484 | 12,4483 | 3,0739 | 20,1035 |
| 2,00 | 1,2629 | 10,0484 | 2,5399 | 11,1381 | 4,6513 | 1,0105 | 17,4373 | 3,3034 | 24,2122 |
| 2,00 | 1,9565 | 11,9251 | 2,8363 | 9,8385 | 4,1702 | 1,1116 | 15,6178 | 2,9417 | 24,5415 |
| 2,80 | 0,6632 | 16,3300 | 3,0883 | 13,1075 | 5,7011 | 1,0241 | 26,4145 | 1,8160 | 37,5915 |
| 2,80 | 0,9798 | 14,8465 | 3,1230 | 13,8199 | 5,6702 | 0,9052 | 26,6948 | 1,7540 | 38,8683 |
| 2,90 | 0,8659 | 17,3987 | 2,4381 | 14,3407 | 5,3830 | 0,4109 | 28,4724 | 2,8899 | 40,3504 |
| 3,00 | 0,5926 | 17,1442 | 1,7274 | 15,7204 | 5,9743 | 0,4929 | 27,3341 | 2,8133 | 40,4670 |
| 3,00 | 0,5223 | 18,8498 | 2,1305 | 15,6550 | 5,7096 | 0,3712 | 28,9271 | 1,9885 | 40,1577 |
| 3,20 | 1,3035 | 18,6170 | 0,2727 | 16,8506 | 5,9244 | 0,6636 | 31,1035 | 1,3586 | 49,6981 |
| 3,20 | 0,3468 | 19,5010 | 0,9072 | 15,2880 | 6,1989 | 0,7557 | 31,9375 | 1,6981 | 48,0468 |
| x | З н а ч е н и я ф у н к ц и и F(x) | ||||||||
| Вар.27 | Вар.28 | Вар.29 | Вар.30 | Вар.31 | Вар.32 | Вар.33 | |||
| -1,80 | 0,7954 | 4,2143 | 2,4855 | 8,4839 | 1,6890 | 7,7193 | 2,9686 | ||
| -1,80 | 0,4751 | 4,1894 | 1,0806 | 8,4528 | 1,9473 | 7,8879 | 2,8571 | ||
| -1,80 | 0,7824 | 4,3386 | 0,2105 | 8,4806 | 1,6229 | 8,0484 | 2,2768 | ||
| -1,00 | 1,0061 | 3,3704 | 3,2685 | 5,1409 | 1,4547 | 6,2831 | 3,0931 | ||
| -0,80 | 1,9167 | 3,1231 | 1,8045 | 5,2923 | 0,7821 | 6,1493 | 3,3069 | ||
| -0,70 | 1,8787 | 2,9799 | 1,3907 | 4,8455 | 0,7107 | 5,6850 | 3,6335 | ||
| -0,20 | 1,7500 | 2,6343 | 2,2458 | 3,5248 | 4,3902 | 5,1625 | 4,0251 | ||
| -0,20 | 1,6736 | 2,6391 | 3,6228 | 3,4686 | 3,0041 | 4,7244 | 4,6314 | ||
| 0,00 | 1,5901 | 2,5917 | 3,0375 | 3,5409 | 5,3968 | 4,6527 | 4,4182 | ||
| 0,50 | 2,4911 | 2,2399 | 5,1021 | 2,6086 | 3,1120 | 3,8518 | 4,8345 | ||
| 1,00 | 2,9704 | 1,6891 | 7,8280 | 2,0339 | 4,2047 | 2,9507 | 6,3153 | ||
| 1,00 | 2,6361 | 1,9321 | 6,4398 | 1,9889 | 5,9370 | 3,4830 | 6,5185 | ||
| 1,30 | 3,6619 | 1,6717 | 9,0353 | 2,1569 | 4,7632 | 3,4173 | 6,6729 | ||
| 2,00 | 4,2837 | 1,2307 | 10,8478 | 0,8357 | 9,6232 | 2,5331 | 8,4478 | ||
| 2,00 | 4,8137 | 1,4651 | 11,4076 | 1,1899 | 5,0399 | 2,6511 | 8,0921 | ||
| 2,20 | 5,0891 | 1,1702 | 11,8879 | 1,3054 | 7,4231 | 2,4445 | 8,4211 | ||
| 2,30 | 4,8418 | 1,2996 | 13,2842 | 1,3476 | 5,9161 | 2,1828 | 8,9484 | ||
| 2,30 | 5,2725 | 1,3972 | 15,4108 | 0,6554 | 6,6441 | 2,2021 | 9,2724 | ||
| 2,70 | 5,5842 | 1,2213 | 18,2798 | 0,6961 | 8,4778 | 1,6939 | 9,8335 | ||
| 2,70 | 5,7598 | 0,9472 | 16,4949 | 1,3209 | 11,6876 | 1,6293 | 10,1606 |
4.6. Контрольные вопросы
1. В каких случаях целесообразно использовать для аппроксимации метод наименьших квадратов?
2. Что минимизируется в методе наименьших квадратов?
3. Зачем в методе наименьших квадратов величина e берется в квадрате?
4. От чего зависит выбор базисных функций в методе наименьших квадратов?
5. Какие базисные функции используются при линейной аппроксимации МНК?
6. Как получены формулы для коэффициентов C и D при экспоненциальной аппроксимации?
ЗАДАЧА 4. Вычисление определенных интегралов
|
из
5.00
|
Обсуждение в статье: Краткие теоретические сведения. В практике обработки экспериментальных данных могут быть ситуации |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

