 |
Главная |
Дифференциальные уравнения колебаний
|
из
5.00
|
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
· Уравнение гармонических колебаний
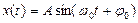 ,
,
где 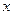 – смещение точки от положения равновесия, А – амплитуда колебаний,
– смещение точки от положения равновесия, А – амплитуда колебаний,  - фаза колебаний, w0– круговая (циклическая частота), t – время,
- фаза колебаний, w0– круговая (циклическая частота), t – время, 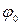 – начальная фаза колебаний.
– начальная фаза колебаний.
 ,
,
где 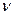 – частота колебаний,
– частота колебаний,  – период колебаний.
– период колебаний.
· Скорость и ускорение при гармонических колебаниях
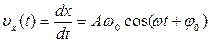 ,
,
 - амплитуда скорости (максимальное значение);
- амплитуда скорости (максимальное значение);
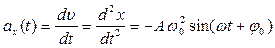 ,
,
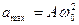 - амплитуда ускорения (максимальное значение).
- амплитуда ускорения (максимальное значение).
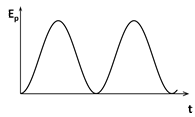
При 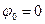 графики зависимостей
графики зависимостей 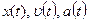 представлены на рис. 1(а,б,в), соответственно.
представлены на рис. 1(а,б,в), соответственно.
· Возвращающая сила
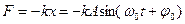 ,
,
где 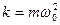 – коэффициент упругой (квазиупругой) силы, m – масса материальной точки;
– коэффициент упругой (квазиупругой) силы, m – масса материальной точки;
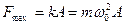 - амплитуда силы (максимальное значение).
- амплитуда силы (максимальное значение).
· Кинетическая энергия колеблющейся точки
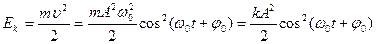
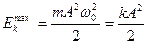 -амплитуда кинетической энергии (максимальное значение).
-амплитуда кинетической энергии (максимальное значение). 

а а 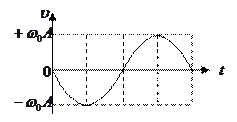
б б 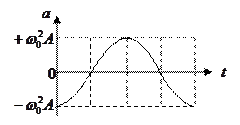

в в
Рис. 1 Рис. 2
· Потенциальная энергия колеблющейся точки

 -амплитуда потенциальной энергии (максимальное значение).
-амплитуда потенциальной энергии (максимальное значение).
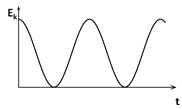
При 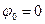 графики зависимостей кинетической и потенциальной энергии от времени представлены на рис. 2а и 2б, соответственно.
графики зависимостей кинетической и потенциальной энергии от времени представлены на рис. 2а и 2б, соответственно.
· Полная энергия при гармонических колебаниях (рис. 2в)
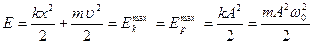 .
.
· Уравнения гармонических колебаний могут быть заданы функциями синуса или косинуса. В таблице 1 даны значения скорости, ускорения, силы и энергии в обоих случаях.
Таблица 1
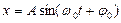
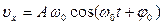
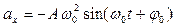
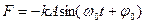
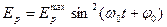

| 
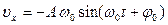
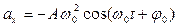

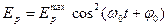
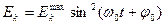
|
· Периоды колебаний:
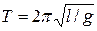 – математический маятник (
– математический маятник ( 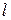 – длина нити);
– длина нити);
 – пружинный маятник (m – масса тела,
– пружинный маятник (m – масса тела, 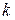 – коэффициент жесткости);
– коэффициент жесткости);
 – физический маятник (
– физический маятник ( 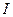 – момент инерции тела относительно оси, проходящей через точку подвеса, определяется по теореме Штейнера, m – масса тела, d – расстояние от точки подвеса до центра масс).
– момент инерции тела относительно оси, проходящей через точку подвеса, определяется по теореме Штейнера, m – масса тела, d – расстояние от точки подвеса до центра масс).
Пример: Однородный диск радиусом  колеблется около горизонтальной оси, проходящей на расстоянии
колеблется около горизонтальной оси, проходящей на расстоянии 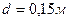 от центра диска. Определить период
от центра диска. Определить период 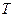 колебаний диска относительно этой оси (рис. 3).
колебаний диска относительно этой оси (рис. 3).
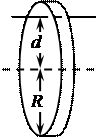 Период определяется по формуле
Период определяется по формуле  , где
, где 

 (нашли по теореме Штейнера). Тогда
(нашли по теореме Штейнера). Тогда
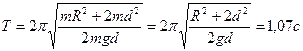 Рис. 3
Рис. 3
· Уравнение затухающих колебаний (рис. 4)
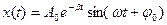 ,
,
где  – амплитуда колебаний в начальный момент времени,
– амплитуда колебаний в начальный момент времени, 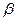 – коэффициент затухания,
– коэффициент затухания, 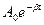 - зависимость амплитуды затухающих колебаний от времени,
- зависимость амплитуды затухающих колебаний от времени, 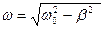 -частота затухающих колебаний,
-частота затухающих колебаний, 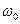 - частота собственных колебаний,
- частота собственных колебаний,  - период затухающих колебаний.
- период затухающих колебаний.

· Уравнение вынужденных колебаний, совершаемых под действием периодически изменяющейся силы 
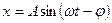 , где
, где
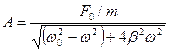 - амплитуда вынужденных колебаний;
- амплитуда вынужденных колебаний;
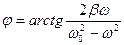 - начальная фаза вынужденных колебаний;
- начальная фаза вынужденных колебаний;
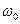 и
и  - частоты собственных и вынужденных колебаний .
- частоты собственных и вынужденных колебаний .
· Резонанс – резкое возрастание амплитуды вынужденных колебаний при частоте, близкой к частоте собственных колебаний.
· Амплитуда при резонансе
 .
.
· Резонансная частота
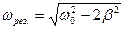 .
.
Дифференциальные уравнения колебаний
 - гармонические,
- гармонические,
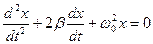 - затухающие,
- затухающие,
 - вынужденные.
- вынужденные.
· Уравнение колебания, полученного при сложении двух колебаний одинаковой частоты и одного направления, амплитуды колебаний которых  и
и 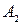 , а начальные фазы
, а начальные фазы  и
и 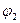 ,
,
 , где
, где
 -
-
амплитуда результирующего колебания, 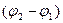 - разность фаз слагаемых колебаний; начальная фаза результирующего колебания определяется формулой
- разность фаз слагаемых колебаний; начальная фаза результирующего колебания определяется формулой
 .
.
· Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с одинаковыми частотами
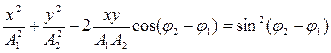 :
:
а) если  , то
, то 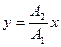 - уравнение прямой,
- уравнение прямой,
б) если 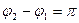 , то
, то 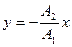 - уравнение прямой,
- уравнение прямой,
в) если 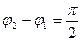 , то
, то  - уравнение эллипса, приведённого к осям,
- уравнение эллипса, приведённого к осям,
г) если 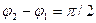 и
и 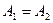 , то
, то  - уравнение окружности, где
- уравнение окружности, где 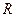 - радиус окружности.
- радиус окружности.
МЕХАНИЧЕСКИЕ ВОЛНЫ
· Длина волны, т.е расстояние между ближайшими частицами, колеблющимися в одинаковой фазе
 ,
,
где 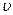 - скорость волны,
- скорость волны, 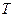 - период,
- период, 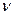 - частота.
- частота.
· Уравнение бегущей волны, распространяющейся вдоль положительного направления оси 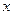 в среде, не поглощающей энергию,
в среде, не поглощающей энергию,
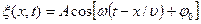 или
или
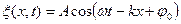 , где
, где
 - амплитуда волны,
- амплитуда волны,  - циклическая частота,
- циклическая частота, 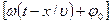 -фаза волны,
-фаза волны, 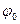 - начальная фаза,
- начальная фаза,  - волновое число.
- волновое число.
Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны. Волна называется поперечной, если частицы колеблются в плоскостях, перпендикулярных направлению распространения волны.
Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т.е. способна сопротивляться деформации сдвига. Этим свойством обладают только твердые тела. Продольные волны могут распространяться как в твердых телах, так и в жидких и газообразных средах.
|
из
5.00
|
Обсуждение в статье: Дифференциальные уравнения колебаний |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

