Построение динамических характеристик разомкнутой системы

2.1. Построение амплитудно-частотной характеристики разомкнутой системы автома­тического управления.

2.2. Опреде­ление устойчивости замкнутой системы и запаса устойчивости по ам­плитуде и фазе по передаточной функции разомкнутой системы автома­тического управления.

Цель: по передаточной функции W_RAZ(p) разомкнутой системы авто­матического управления построить амплитудно-фазовую частотную ха­рактеристику и определить, используя критерий Найквиста, устойчи­вость замкнутой системы и запас устойчивости по амплитуде и фазе.

Критерий Найквиста позволяет оценивать устойчивость замкнутой системы по амплитудно-фазовой частотной характеристике разомкнутой системы.

Формулировка критерия Найквиста:

если система устойчива в разомкнутом состоянии, то для устойчивости соответствующей замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы для частот 0≤ω≤∞ не охватывала на комплексной плоскости точку с координатами(-1, j 0).

Рис. 1. АФЧХ систем с различной устойчивостью.

Запас устойчивости системы по амплитуде и фазе можно определить по удаленности амплитудно-фазовая частотной характеристики от критической точки с координатами(-1, j 0).

Передаточная функция разомкнутой системы:

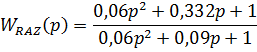
Для построения амплитудно-частотной характеристики разомкнутой системы автома­тического управления примем р = ωj, тогда:

Отделяем в выражении числителя и знаменателя действительную и мнимую части:

Re(ω) = 1-0,06

Im(ω) = 0,09ω

Таким образом: Y=1- 0,06 +0,09ω (1)

Используя (1) для числителя и знаменателя разомкнутой функции получаем:

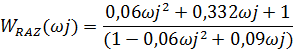
Для того, чтобы разделить передаточную функцию на действительную и мнимую составляющие, воспользуемся правилом:

В общем виде частотная передаточная функция САУ:

Числитель и знаменатель состоят из действительных и мнимых членов. Приmиn – нечетных составляющие полиномов являют­ся мнимыми значениями, поскольку (j)^m = (j)ⁿ = (±)j. При четных mи n получим действительные значения. В этом случае можно напи­сать:

Для выделения в этом комплексном числе действительной и мни­мой части необходимо умножить числитель и знаменатель на комплексно-сопряженное значение знаменателя:

(2)

Это выражение можно представить в виде двух слагаемых

В последнем выражении для передаточной функции можно выделить действительную Rе(ω) и мнимую – Im(ω) части.

В соответствии с (2) умножаем числитель и знаменатель на комплексно-сопряженное значение знаменателя – для нашего случая:

(1- 0,06 -j0,09 ω)

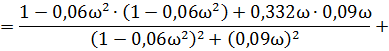
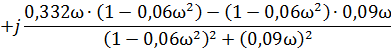
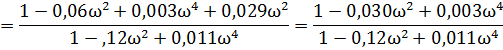
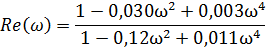
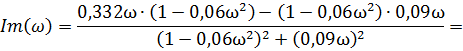
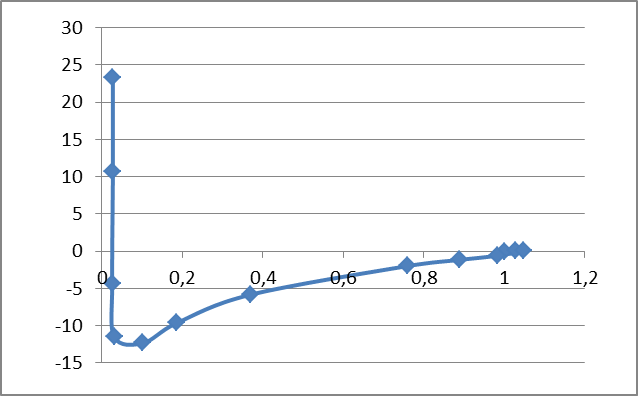
Рис. 1. Амплитудно-фазовая частотная характеристика разомкнутой системы.

По построенной Амплитудно-фазовой частотной характеристики разомкнутой системы можно сделать вывод, что система устойчива не только в разомкнутом, но и в замкнутом состоянии, т.к. амплитудно-фазовая частотная характеристика для частот 0≤ω≤∞ не охватывает на комплексной плоскости точку с координатами(-1, j 0).

Запас устойчивости системы по амплитуде и фазе можно определить по удаленности амплитудно-фазовая частотной характеристики от критической точки с координатами(-1, j 0) (рис. 2).

Запас устойчивости по фазе равен значению угла λ для частоты среза ω, при которой |W(ω)|=1. Запас устойчивости по амплитуде ра­вен значению величины отрезка h оси абсцисс между точкой (-1, j0) и амплитудно-фазовой частотной характеристикой. Величину запаса устойчивости по амплитуде можно вычислить по формуле:

.

Запас по амплитуде должен быть не менее 6 дБ (З_h ≥6 дБ).

Запас устойчивости по фазе – это дополнительный сдвиг фазы («поворот» Амплитудно-фазовой частотной характеристики против часовой стрелки), который необходим для того, чтобы вывести систему на границу устойчивости. Он определяется на частоте среза ω_с, где |W(ω)|=1. Запас по фазе должен быть не менее 30°.

Для рассматриваемого примера запас устойчивости системы по амплитуде h = 1 – это много более 6 дБ; запас устойчивости по фазе λ = 266° – много более 30°.