 |
Главная |
Построение Амплитудно-частотной характеристики разомкнутой системы
|
из
5.00
|
Значений амплитуды А (ω) в зависимости от частоты:
А (ω) = [Rе2(ω) + Im2(ω)]0,5

Рис. 3. Амплитудно-частотная характеристика разомкнутой системы.
Построение фазо-частотной характеристики разомкнутой системы.
Значений фазы φ (ω) в зависимости от частоты:
φ (ω) = arctg [Im(ω) / Rе(ω)]
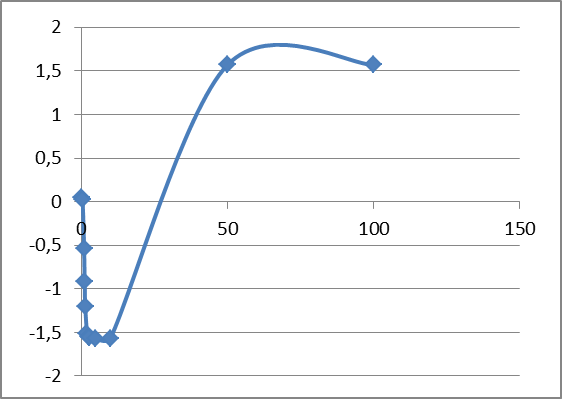
Рис. 4. Фазо-частотная характеристика разомкнутой системы.
Построение логарифмических частотных характеристик разомкнутой системы.
Логарифмические частотные характеристики – эффективное средство анализа и синтеза систем автоматического регулирования. Они определяют сравнительно простую связь между динамическими характеристиками отдельных элементов и системы в целом, особенно при исследованиях разомкнутых систем автоматического регулирования с последовательно соединенными звеньями. Амплитудно-частотная и фазо-частотная характеристики разомкнутой системы с последовательно соединенными звеньями представляют собой сумму соответственно логарифмических амплитудных и фазовых частотных характеристик звеньев системы, что очень удобно при их вычислении, особенно графическим способом.
Для получения логарифмической частотной характеристики следует прологарифмировать передаточную функцию. При этом получим следующую зависимость:
ln W (jω) = ln A (ω) + jφ (ω)
Натуральный логарифм частотной характеристики ln A (ω) имеет две составляющие. В практических целях вместо натурального логарифма удобнее использовать десятичный логарифм:
AL (ω) = 20lg A(ω)
Коэффициент 20 используется для получения результата в децибелах.
Характеристики ЛАЧХ (логарифмическая амплитудно-частотная характеристика) и ЛФЧХ (логарифмическая фазо-частотная характеристика) строятся следующим образом: по оси абсцисс в логарифмическом масштабе откладывается частота ω, а по оси ординат в линейном масштабе – отношение амплитудAL (ω) (в децибелах) и фаз φL (ω) (в градусах).
ЛФЧХ определяют по формуле: 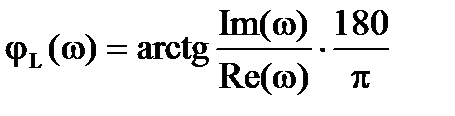
Построение логарифмической амплитудно-частотной характеристики (ЛАЧХ).
Значения ЛАЧХ определяют по формуле: AL (ω) = 20lg A(ω).

Рис. 5. Логарифмическая амплитудно-частотная характеристика (ЛАЧХ).
Построение логарифмической фазо-частотной характеристики (ЛФЧХ).
Значения ЛФЧХ определяют по формуле:  .
.

Рис. 6. Логарифмическая фазо-частотная характеристика (ЛФЧХ).
Таблица 1.
Значения Rе(ω), Im(ω), А (ω), φ (ω), AL (ω), φ L (ω) в зависимости от частоты ω.
| А | В | С | D | Е | F | G | H | |
| ω | Rе(ω) | Im(ω) | А (ω) | φ (ω) | AL (ω) | φ L (ω) | t | |
| 0,25 | 1,028551 | 0,04808 | 1,029674 | 0,046712 | 0,253999 | 2,677745 | ||
| 0,5 | 1,048383 | 0,021668 | 1,048607 | 0,020665 | 0,412253 | 1,184604 | ||
| 0,982828 | -0,59053 | 1,146592 | -0,54104 | 1,188181 | -31,0151 | |||
| 1,2 | 0,888317 | -1,16706 | 1,466675 | -0,92019 | 3,326675 | -52,7499 | ||
| 1,4 | 0,7594 | -1,98661 | 2,126807 | -1,20568 | 6,554563 | -69,1152 | ||
| 0,368254 | -5,84479 | 5,856376 | -1,50787 | 15,35258 | -86,4386 | |||
| 2,5 | 0,186054 | -9,63513 | 9,636928 | -1,55149 | 19,67877 | -88,9388 | ||
| 0,101885 | -12,3303 | 12,33071 | -1,56253 | 21,81977 | -89,572 | |||
| 0,03073 | -11,5148 | 11,51482 | -1,56813 | 21,22514 | -89,8927 | |||
| 0,025459 | -4,33953 | 4,339601 | -1,56493 | 12,749 | -89,7093 | |||
| 0,027165 | 10,65445 | 10,65448 | 1,568247 | 20,55065 | 89,89949 | |||
| 0,027246 | 23,32727 | 23,32728 | 1,569628 | 27,35728 | 89,9787 | |||
|
из
5.00
|
Обсуждение в статье: Построение Амплитудно-частотной характеристики разомкнутой системы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

