 |
Главная |
Построение динамических характеристик замкнутой системы
|
из
5.00
|
По ранее выполненным вычислениям передаточная функция замкнутой системы:

Для построения амплитудно-частотной характеристики замкнутой системы автоматического управления примем р = ωj, тогда:

Дальнейшие вычисления и построения осуществляем по аналогии с разомкнутой системой автоматического управления.
Отделяем в выражении числителя и знаменателя действительную и мнимую части:

Для выделения в этом комплексном числе действительную и мнимую части необходимо умножить числитель и знаменатель на комплексно-сопряженное значение знаменателя: 



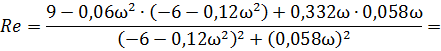







Построение Амплитудно-фазовой частотной характеристики замкнутой системы.

Рис. 7. Амплитудно-фазовая частотная характеристика замкнутой системы.

Рис. 8. Амплитудно-частотная характеристиказамкнутой системы.

Рис. 9. Фазо-частотная характеристиказамкнутой системы.

Рис. 10. Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) замкнутой системы.

Рис. 11. Логарифмическая фазо-частотная характеристика (ЛФЧХ) замкнутой системы.
Таблица 2.
Значения Rе(ω), Im(ω), А (ω), φ (ω), AL (ω), φ L (ω), Re D(jω), im D(jω) для замкнутой системы автоматического управления в зависимости от частоты ω
| А | В | С | D | Е | F | G | H | I |
| ω | Rе(ω) | Im(ω) | А (ω) | φ (ω) | AL (ω) | φ L (ω) | Re D(jω) | im D(jω) |
| 0,25 | 0,25 | |||||||
| 0,25 | 0,250052 | -0,0173 | 0,250649 | -0,06908 | -12,0187 | -3,95986 | 8,99625 | 0,083 |
| 0,5 | 0,250202 | -0,03424 | 0,252534 | -0,13601 | -11,9536 | -7,79652 | 8,985 | 0,166 |
| 0,250734 | -0,06569 | 0,259196 | -0,25622 | -11,7274 | -14,6879 | 8,94 | 0,332 | |
| 1,2 | 0,250998 | -0,07694 | 0,262525 | -0,29743 | -11,6166 | -17,0503 | 8,9136 | 0,3984 |
| 1,4 | 0,251266 | -0,08724 | 0,26598 | -0,33418 | -11,503 | -19,1569 | 8,8824 | 0,4648 |
| 0,251908 | -0,11164 | 0,275539 | -0,41717 | -11,1963 | -23,9142 | 8,76 | 0,664 | |
| 2,5 | 0,251979 | -0,12392 | 0,280804 | -0,45707 | -11,0319 | -26,2014 | 8,625 | 0,83 |
| 0,251356 | -0,12899 | 0,282523 | -0,47414 | -10,9789 | -27,1802 | 8,46 | 0,996 | |
| 0,239617 | -0,09585 | 0,258075 | -0,38051 | -11,7651 | -21,8125 | 7,5 | 1,66 | |
| 0,171429 | 0,053571 | 0,179604 | 0,302885 | -14,9137 | 17,36283 | 3,32 | ||
| 0,014878 | 0,073712 | 0,075198 | 1,371626 | -22,4758 | 78,62826 | -141 | 16,6 | |
| 0,003853 | 0,039184 | 0,039373 | 1,472772 | -28,096 | 84,42641 | -591 | 33,2 |
Устойчивость системы.
Автоматическая система считается устойчивой, если она занимает требуемое состояние (положение) и остается в нем по желанию пользователя. В противном случае АС будет неустойчивой.
Существует много критериев устойчивости объекта в зависимости от типов его моделей. Для линейных объектов применяют два подхода к определению устойчивости:
− прямой (непосредственный);
− косвенный.
При прямом подходе записывают любой процесс управления и, зная его желаемое состояние, исходя из определения устойчивости и неустойчивости, делают заключения о его качествах.
Однако прямой метод исследования устойчивости объекта не всегда целесообразен, а иногда и невозможен. Это бывает в случае, когда пользователь работает только с его математической моделью, в виде, например, дифференциальных уравнений, передаточных функций и т.д. В этой ситуации для исследования устойчивости объекта используются обычно следующие косвенные методы:
− алгебраический;
− корневой;
− частотный.
Количественная оценка устойчивости систем производится с помощью системы показателей, характеризующих запас устойчивости. Запас устойчивости – это количественная характеристика степени удаления системы от границы устойчивости.
Обеспечение запаса устойчивости необходимо по следующим причинам:
при составлении уравнений связи отдельных элементов допускается некоторая идеализация протекающих в них физических процессов (учитываются только главные факторы и отбрасываются второстепенные);
− линеаризация нелинейных уравнений приводит к их еще большей приближенности;
− конструктивные параметры элементов, входящие в коэффициенты уравнений, определяются с некоторой погрешностью;
− при эксплуатации систем возможны изменения параметров элементов вследствие температурных колебаний, старения, нестабильности и т.д.
Наличие определенного запаса устойчивости гарантирует сохранение устойчивости системы при изменении ее параметров в определенных пределах.
Чем больше запас устойчивости, тем меньше вероятность того, что система в процессе эксплуатации станет неустойчивой. Запас устойчивости необходим еще и потому, что он определяет характер переходных процессов в системах. Наличие определенного запаса устойчивости обеспечивает работу реальной системы в области устойчивости с требуемым качеством переходного процесса.
Различаются следующие основные показатели запаса устойчивости:
− запас устойчивости по амплитуде;
− запас устойчивости по фазе;
Формулировки показателей устойчивости:
Устойчивость АС – свойство системы обеспечить сколь угодно малое отклонение возмущенного движения при достаточно малых начальных возмущениях за конечный отрезок времени.
Критерии устойчивости АС – математически сформулированные правила, позволяющие исследовать устойчивость системы без вычисления корней характеристического уравнения.
Характеристическое уравнение системы – уравнение, получаемое приравниванием к нулю числителя или знаменателя передаточной функции системы (характеристического многочлена дифференциального уравнения). Соответственно, получается характеристическое уравнение разомкнутой и замкнутой систем.
|
из
5.00
|
Обсуждение в статье: Построение динамических характеристик замкнутой системы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

