 |
Главная |
Распределение Максвелла
|
из
5.00
|
Очевидно, что совершенно такие же распределения должны быть и по другим компонентам скорости:
dn/ndvx = Ae[D3]
dn/ndvy = Ae[D4]
Теперь нужно найти вероятность того, что скорости молекул удовлетворяют трем условиям:
vx лежит в пределах от vx до vx+dvx , vy лежит в пределах от vy до vy+dvy , а vz лежит в пределах от vz до vz+dvz. Значения составляющих скоростей молекул по каждой из осей координат не зависят от значений по другим осям. Поэтому, вероятность того, что скорость молекулы одновременно удовлетворяет трем условиям является «вероятностью сложного события», т.е. равна произведению вероятностей.
Если обозначить число молекул в единице объема газа dnxyz с составляющими по осям dnx, dny, dnz ,то
dnxyz/n = A3e[D5] dvxdvydvz v2 = Σ(vi)2
Эта формула показывает, сколько молекул из числа находящихся в единице объема обладают скоростями, составляющие которых по осям координат лежат в интервале между vx и vx+dvx, vy и vy+dvy, vz и vz+dvz , т.е. обладают скоростью, лежащей в интервале заданном и по величине и по направлению. Нам в распределении необходимо учесть все любые направления движения.
Если собрать все молекулы единицы объема газа со скоростями в интервале от v до v+dv по всем любым направлениям и выпустить их, то они, разлетаясь по всем направлениям, через 1 с окажутся равномерно распределенными в шаровом слое радиусом v и толщиной dv. Число молекул в единице объема этого слоя (объем скоростей) такое же, как и в параллелепипеде объемом dvxdvydvz. Число же молекул во всем слое – это и есть число молекул в единице объема газа, независимо от направления, скорости которых лежат в интервале от v до v+dv:
dn = n(m/2πkT)3/2e[D6] dΩ; dΩ = 4πv2dv, отсюда:

 dn/n =( 4/√π )(m/2kT) 3/2e[D7] dv
dn/n =( 4/√π )(m/2kT) 3/2e[D7] dv
Это и есть закон Максвелла распределения молекул по скоростям.
dn/n – вероятность того, что у произвольно выбранной молекулы газа скорость окажется лежащей в интервале от v до v+dv, т.е. это доля всех мол. ед. объема, скорости кот. лежат в интервале от v до v+ dv.
 Величина f(v) = dn/ndv = (4/√
Величина f(v) = dn/ndv = (4/√  π )(m/2kT) 3/2e[D8] dv –функция распределения молекул по скоростям.
π )(m/2kT) 3/2e[D8] dv –функция распределения молекул по скоростям.
Она определяет долю молекул в единице объема, скорости которых заключены в единичном интервале скоростей вблизи v, включающем данную скорость.
f(v) обращается в 0 при v = 0 и v = ∞, т.е., нет неподвижных молекул и нет молекул с бесконечно большой скоростью. Имеется максимум при vн, т.е. наибольшая часть молекул движется со скоростью v ≈ vн, т.е. вероятность того, что молекула имеет скорость vн – наибольшая, поэтому vн называют наиболее вероятной скоростью.
Пользуясь кривой распределения молекул по скоростям можно графически найти долю молекул dn/n в единице объема газа, скорости которых лежат в заданном интервале скоростей dv. Графически - это площадь с основанием dv и высотой f(v). Вся площадь под кривой f(v) дает нам общее число молекул в единице объема.
Вид кривой зависит от природы газа и от Т. С повышением Т максимум смещается в сторону больших скоростей, но площадь под кривой остается постоянной, т.к. n = const.
При выводе распред. Максвелла по скоростям совершенно не принимали во внимание столкновения молекул между собой, хотя они изменяют скорость и влияют на распределение. В действительности именно благодаря столкновениям и устанавливается максвелловское распределение по скоростям. При каждом столкновении скорость одной молекулы увеличивается, другой уменьшается. Максвелл предположил, что равновесному состоянию отвечает такое, при котором число молекул, скорости которых увеличиваются при столкновении равно числу молекул, скорости которых уменьшаются при столкновениях. Такому состоянию и соответствует распределение Максвелла.
Позже Больцман показал, что если газ находится в состоянии с немаксвелловским распределением, то благодаря столкновениям он сам собой переходит в состояние с максвелловским распределением.
Распределение Максвелла (иногда говорят Максвелла -Больцмана) – это равновесное распределение. Теперь можно дать определение хаотичному движению:
движение молекул полностью хаотично, если скорости распределены по закону Максвелла.
Распределение М. и Б. можно объединить в один закон – М-Б, согласно которому число молекул, компоненты скорости которых лежат в интервале от vx, vy, vz до vx+dvx….., а координаты в пределах от x, y, z до x+dx,….. равно dN(vx, vy, vz, x,y,z) = Aexp(-(Еp+mv2/2)/kT) dvxdvydvzdxdydz;
Здесь Ер и Екин = mv2/2 могут принимать непрерывный ряд значений.
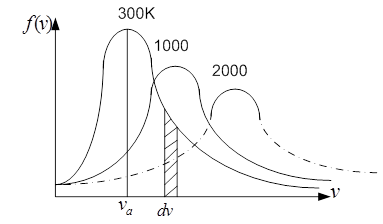 рис.16
рис.16
|
из
5.00
|
Обсуждение в статье: Распределение Максвелла |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

