Идеальный газ. Уравнение состояния

Молекулярная физика и

Термодинамика

сборник методических указаний

для самостоятельной работы студентов БГИТА

дневного и заочного обучения

 

 

Брянск 2005

 

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное агентство по образованию

 

 

Брянская государственная инженерно-технологическая академия

 

Кафедра физики

 

 

УТВЕРЖДЕНО

Редакционный совет БГИТА

 

Протокол №___ от "__"________г.

 

Молекулярная физика и

Термодинамика

 

сборник методических указаний

для самостоятельной работы студентов БГИТА

дневного и заочного обучения

 

 

Брянск 2005

 

Составители: ст. преподаватель кафедры физики БГИТА, Матанцева В.А.

ассистент кафедры физики БГИТА Притыченко Л.М.

 

Рецензент: зав. кафедрой математики, доцент, к.ф-м.н. Баранова И.М.

 

 

Рекомендованы редакционно-издательской комиссией

строительного факультета

 

Протокол № ___ от " __" _________г.

 

Содержание

 

	Стр.
Введение…………………………………………………………….
1. Идеальный газ. Уравнение состояния Идеального Газа. Газовые законы…………………………………………
2. Изопроцессы в Идеальном Газе…………………………
3. Основы молекулярно – кинетической теории газов………………………………………………………………………
4. Явления переноса в термодинамических неравновесных системах…………………………………………….….
5. Основы термодинамики…………………………………...
6. Круговые процессы. Цикл Карно………………………..
7. ЭНТРОПИЯ. II И III НАЧАЛА ТЕРМОДИНАМИКИ……………
8. Реальные газы. Жидкости ………………………………….
9. Примеры решения задач…………………………………….
10. Литература………………………………………………………

 

 

Введение

Любое тело с точки зрения молекулярной физики можно представить как совокупность огромного числа частиц. Поэтому описывать свойства такого тела – системы частиц - целесообразно с помощью усредненных значений физических величин – скорости, импульса, энергии. Вместе с тем, систему как целое можно характеризовать такими понятиями как масса, количество вещества, давление, температура, внутренняя энергия и т.д.

В любом случае описание и исследование свойств системы частиц удобно проводить с помощью модели термодинамической системы, характеризуемой термодинамическими параметрами.

 

Идеальный газ. Уравнение состояния

Идеального Газа. Газовые законы

Простейшей моделью термодинамической системы является идеальный газ.

Идеальным газом называют газ, в котором: собственные размеры молекул пренебрежимо малы по сравнению с размером сосуда; отсутствует взаимодействие между молекулами (т.е. потенциальная энергия взаимного притяжения молекул пренебрежимо мала); соударения молекул со стенками сосуда – абсолютно упругие.

Идеальный газ (как и любое вещество) можно характеризовать величинами:

-количество вещества ; 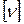= моль;

; или ; или при нормальных условиях ;

где: N – общее число молекул в данной системе; - постоянная Авогадро (число частиц в одном моле вещества); - масса данной системы; - молярная масса вещества (см. ниже); 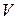- объем, занимаемый веществом; - объем одного моля вещества;

При нормальных условиях 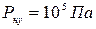и

;

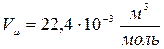- молярная масса вещества; ;

;

где: - относительная молекулярная масса, определяемая по химической формуле вещества; - размерный коэффициент в системе СИ.

Также .

Для смеси газов ;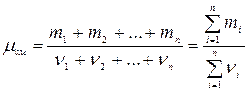

где и 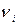- соответственно масса и количество вещества i-того компонента смеси; n – число компонентов смеси.

Массовая доля i-того компонента смеси

 

,

где - масса смеси.

Термодинамическими параметрами идеального газа являются объем, давление и температура.

Объемомназывается часть пространства, занимаемая телом

Для термодинамической системы (идеального газа) объемом может служить объем сосуда, в котором она находится. ;

Давление – скалярная физическая величина, численно равная силе, приходящейся на единицу площади поверхности, на которую эта сила нормально действует:

; = Па (паскаль)

Для термодинамической системы давление обусловлено совокупным действием молекул на дно и стенки сосуда.

Для смеси газов справедлив закон Дальтона:

,

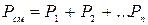где - парциальное давление i-го компонента смеси; n – число компонентов смеси.

Температура – мера интенсивности теплового движения частиц системы, находящейся в равновесном состоянии.

(кельвин) - по термодинамической температурной шкале.

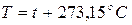- взаимосвязь между термодинамической и стоградусной шкалой Цельсия.

Уравнение, связывающее термодинамические параметры, является уравнением состояния термодинамической системы. Основным уравнением состояния ИГ является уравнение Менделеева-Клапейрона:

 

(1.1)

 

где: - универсальная газовая постоянная.

Домножив и поделив левую часть (1.1) на , а также поделив на V, получим:

(1.2)

где: 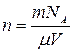- концентрация молекул; - постоянная Больцмана