Реальные газы. Жидкости

Между молекулами вещества действуют силы взаимного притяжения и отталкивания. Они проявляются на расстояниях 10^-9 м и являются короткодействующими. На некотором расстоянии r₀ между молекулами силы отталкивания и притяжения уравновешивают друг друга и молекулы находятся в состоянии устойчивого равновесия, обладая минимальной потенциальной энергией Е_min. Соотношение между Е_min и энергией теплового движения kT является критерием существования различных агрегатных состояний вещества:

при Е_min << kT –газообразное с хаотическим расположением молекул;

при Е_min >> kT –твердое с "дальним" порядком расположения молекул;

при Е_min kT –жидкое с "ближним" порядком расположения молекул.

Любое вещество, в зависимости от температуры может находиться в газообразном, жидком или твердом состоянии, причем температура перехода из одного состояния в другое зависит от Е_min для данного вещества.

Для реальных газов необходимо учитывать силы межмолекулярного взаимодействия, а также собственный объем молекул. Наличие этих факторов изменяет вид уравнения состояния реального газа. Оно принимает вид:

(8.1)

Это уравнение называется уравнением Ван – дер – Ваальса. Здесь: - добавочное давление, возникающее за счет сил взаимодействия между молекулами; - суммарный собственный объем всех молекул; a,b - поправки на давление и объем соответственно, определяемые для данного газа экспериментально; ν - число молей реального газа.

Для реального газа характерно наличие критических параметров Т_к, V_к и P_к.

При температуре реального газа Т > Т_к он становится аналогичным идеальному. Критические параметры связаны с поправками :

; ; (8.2)

Внутренняя энергия реального газа складывается из кинетической энергии теплового движения молекул и потенциальной энергии их взаимодействия:

(8.3)

Знак "-" в (8.3) означает, что силы, создающие добавочное давление в реальных газах, являются силами притяжения.

 

Поверхностное натяжение жидкостей. Капиллярные явления.

При "ближнем" порядке расположения молекулы, находящиеся внутри жидкости испытывают действие со стороны соседних молекул, находящихся в сфере молекулярного действия с радиусом (рис.8.1). На молекулу 1 действуют силы, направленные в разные стороны и одинаковые по величине, т.е. скомпенсированные.

Однако на молекулу 2, находящуюся в поверхностном слое таких же молекул действуют силы, равнодействующая которых не равна нулю и направлена внутрь жидкости. Поэтому молекулы поверхностного слоя оказывают на жидкость давление, называемое внутреннимили молекулярным. Силы, создающие это давление, называются силами поверхностного натяжения. Полная энергия частиц жидкости складывается из энергии их хаотического движения и энергии их взаимодействия. Работа по перемещению молекул из глубины совершается за счет их кинетической энергии и приводит к увеличению их потенциальной энергии. Поэтому молекулы в поверхностном слое обладают потенциальной энергией, большей на величину поверхностной энергии :

, (8.4)

где - коэффициент поверхностного натяжения данной жидкости, - площадь поверхностного слоя.

Условием устойчивого равновесия молекул поверхностного слоя является минимум их поверхностной энергии, и за счет сил поверхностного натяжения площадь поверхностного слоя будет сокращаться. Сила поверхностного натяжения F, действующая на протяжении длины l контура поверхностного слоя, пропорциональна l:

, (8.5)

откуда , или из (8.4)

т.е. коэффициент поверхностного натяжения – это сила поверхностного натяжения, действующая на единице длины контура поверхностного слоя.

При сокращении площади поверхностный слой искривляется, что приводит к возникновению добавочного давления под искривленной поверхностью:

, (8.6)

где R – радиус кривизны поверхности.

Если поверхность жидкости выпуклая, то Δр > 0; если вогнутая, то Δр < 0 (рис. 8.2). В случае плоской поверхности силы поверхностного натяжения добавочного давления не создают.

В общем случае избыточное давление под искривленной поверхностью жидкости любой формы определяется по формуле:

, (8.7)

где R₁ и R₂- радиусы кривизны двух нормальных взаимно перпендикулярных сечений поверхности; "+" соответствует выпуклой поверхности, "-" - вогнутой.

Искривленная свободная поверхность жидкости, помещенной в сосуд, называется мениском. Линия, по которой мениск пересекается с твердой стенкой сосуда, называется периметром смачивания (рис. 8.3). Мениск характеризуется углом θ между смоченной поверхностью стенки и касательной к искривленной поверхности жидкости. Угол θ называется краевым углом. При θ < π/2 (рис.8.3, а) жидкость смачивает поверхность, при θ > π/2 (рис.8.3, б) - не смачивает. При θ = 0 (рис.8.3, в) проявляется полное смачивание, при θ ≈ π (рис. 8.3, г) – полное несмачивание.

 

 

Явление смачивания (или несмачивания) обеспечивает высоту поднятия жидкости в узких сосудах – капиллярах: уровень жидкости в капилляре выше, чем в широком сосуде при смачивании, и ниже при несмачивании. Высота поднятия h жидкости в капилляре такова, что давление столба жидкости уравновешивается добавочным давлением под искривленной поверхностью (рис 8.4).

ρgh = 2σ/R (8.8)

 

Как видно из рис. 8.4, R =r/cos θ, поэтому ρgh = 2σcos θ/r;

 

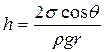, (8.9)

 

где ρ - плотность жидкости, σ - коэффициент поверхностного натяжения, r - радиус капилляра, R- радиус кривизны мениска.

Выражение (8.9) носит название формулы Жюрена.

 

 

Примеры решения задач

Пример 1.В баллонах вместимостью V₁ = 20 л и V₂ = 44 л содержатся газы. Давление в первом баллоне P₁ = 2,4 МПа, во втором P₂ = 1,6 МПа. Определить общее давление P и парциальные давления P₁´ и P₂´ после соединения баллонов, если температура газа осталась неизменной.

 

Решение:

При соединении баллонов произошел изотермический переход газов в новые состояния:

P₁V₁ = P₁´(V₁+V₂) (1.1)

P₂V₂ = P₂´(V₁+V₂) . (1.2)

Выразим Р₁´ и Р₂´

P₁´= P₁V₁/(V₁+V₂) (1.3)

P₂´= P₂V₂/(V₁+V₂), (1.4)

где P₁´, P₂´ - парциальные давления в смеси.

Общее давление по закону Дальтона, P = P₁´+ P₂´, т.е.

P = (P₁V₁ + P₂V₂)/( V₁ + V₂) (1.5)

Формулы (1.3), (1.4), (1.5) являются расчетными для искомых величин.

Произведем вычисления:

P = (2,4 · 10⁶ · 20 · 10^-3 + 1,6 · 10⁶ · 44 · 10^-3)/(20 · 10^-3 + 44 · 10^-3 =

= 1,85 · 10⁶ (Па) = 1,85 МПа

P₁´=2,4 · 10⁶ · 20 · 10^-3/(20 · 10^-3 + 44 · 10^-3) = 0,75 · 10⁶ (Па) = 0,75 МПа

P₂´=1,6 · 10⁶ · 44 · 10^-3/(20 · 10^-3 + 44 · 10^-3) = 1,1 · 10⁶ (Па) = 1,1 МПа

Ответ: P = 1,85 МПа; P₁´ = 0,75 МПа; P₂´= 1,1 МПа.

 

Пример 2. Определить кинетическую энергию <ε₀>, приходящуюся в среднем на одну степень свободы молекулы азота при температуре Т = 1кК, среднюю кинетическую энергию <ε_n> поступательного движения, вращательного движения <ε_в>, среднее значение полной кинетической энергии <ε> молекулы, среднюю квадратичную скорость движения молекул <v_кв>.

 

Решение:

По закону о равномерном распределении энергии по степеням свободы, на каждую степень свободы в среднем приходится энергия

(2.1)

Среднее значение полной кинетической энергии <ε> молекулы равно:

, (2.2)

где i - полное число степеней свободы молекулы.

Молекула азота – двухатомная, т.е. i = 5, причем из них 3 поступательных и 2 вращательных степеней свободы. Поэтому для <ε_n> и <ε_в> можно записать:

; (2.3)

. (2.4)

Средняя квадратичная скорость движения молекул определяется:

.

Вычислим искомые величины:

<ε₀> = 1,38 · 10^-23 · 0,5 · 10³ = 0,69 · 10^-20 (Дж)

<ε> = 5 · <ε₀> = 3,45 · 10^-20 (Дж)

<ε_n> = 3 · <ε₀> = 2,07 · 10^-20 (Дж)

<ε_в> = 2 · <ε₀> = 1,38 · 10^-20 (Дж)

<v_кв> = 0,9444 ·10³ = 944 (м/с)

 

Ответ: <ε₀> = 0,69 · 10^-20 Дж; <ε> = 3,45 · 10^-20 Дж; <ε_n> = 2,07·10^-20 Дж;

<ε_в> = 1,38 · 10^-20 Дж; <v_кв> = 944 м/с.

 

Пример 3. Определить среднюю арифметическую скорость молекул газа <v>, если их средняя квадратичная скорость <v_кв> = 1км/с.

 

Решение:

Для названных в условии скоростей можно записать:

, (3.1)

. (3.2)

Из (3.1): . (3.3)

Подставляя (3.3) в (3.2), получим

.

Таким образом,

.

Ответ: <v> = 0,92 км/с.

 

Пример 4.Какое количество теплоты теряет помещение за время t = 1 час через окно за счет теплопроводности воздуха, заключенного между рамами? Площадь каждой рамы S = 4 м² , расстояние между ними d = 30 см. Температура помещения t₁ = 18⁰ С, температура наружного воздуха t₂ = - 20 ⁰ С. Диаметр молекул воздуха = 0,3 нм. Температуру воздуха между рамами считать средним арифметическим температур помещения и наружного воздуха. Давление P = 101,3 кПа.

 

Решение:

Потери тепла происходят за счет теплопроводности по закону Фурье:

(4.1)

где 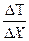- градиент температуры и, в данном случае, это разность температур внутри и снаружи помещения:

. (4.2)

Коэффициент теплопроводности воздуха определяется из молекулярно-кинетической теории:

. (4.3)

 

 

Удельная теплоемкость с_v:

 

- для воздуха (i = 5)

- плотность воздуха между рамами

- средняя арифметическая скорость молекул воздуха

- средняя длина свободного пробега молекул

- концентрация молекул воздуха между рамами

Таким образом,

. (4.4)

 

Подставив (4.4), (4.2) в (4.1), с учетом данных задачи найдем искомую величину:

 

. (4.5)

Так как, по условию, 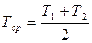, то, преобразовав (4.5) к виду, удобному для вычисления, получим:

 

. (4.6)

Вычислим отдельно коэффициент теплопроводности λ:

 

 

.

 

Тогда

.

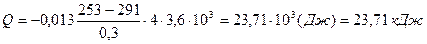Ответ: Q = 23,71 кДж

 

Пример 5.Масса m = 10г кислорода находится при давлении р = 0,3 МПа и температуре t = 10 ⁰ C. После нагревания при р = const газ занял объем V₂ = 10 л. Найти количество теплоты Q, полученное газом, и энергию теплового движения молекул газа W до и после нагревания.

 

Решение:

По 1-ому закону термодинамики

Q = (5.1)

где - изменение внутренней энергии, А - работа по изменению объема.

Для изобарного процесса можно также записать:

, (5.2)

где и Т₂ найдем из закона Гей-Люссака

(5.3)

Находим предварительно из уравнения Менделеева - Клапейрона объем V₁

; , (5.4)

где .

Из (5.3) и (5.4):

(5.5)

Тогда

(5.6)

Подставим (5.6) в (5.2):

(5.7)

В (5.7) все величины известны: i = 5 – число степеней свободы для кислорода (двухатомный газ); кг/моль – молярная масса кислорода.

Вычислим Q:

 

 

По формуле (5.5) вычислим температуру Т₂:

 

.

 

Энергия теплового движения молекул W до и после нагревания – это внутренняя энергия при температурах Т₁ и Т₂:

(5.8)

(5.9)

Поэтому:

Ответ: Q = 7,66 кДж; W₁ = 1,8 кДж; W₂ = 7,5 кДж.

 

 

Пример 6. Найти среднюю арифметическую < v >, среднюю квадратичную < v_кв > и наиболее вероятную v_в скорости движения молекул газа, который при давлении P = 40 кПа имеет плотность ρ = 0,3 кг/м³.

 

Решение:

Из молекулярно-кинетической теории идеального газа известно, что

 

, (6.1)

, (6.2)

. (6.3)

 

Из уравнения Менделеева-Клапейрона получаем:

 

; ; . (6.4)

Тогда

, (6.1 а)

, (6.2 а)

. (6.3 а)

 

 

Вычислим искомые величины:

 

 

 

Ответ: < v > = 583 м/с; < v_кв > = 632 м/с; v_в = 516 м/с.

 

 

Пример 7.Найти удельные теплоемкости и смеси газов, состоящей из 3 кмолей аргона и 2 кмолей азота.

 

Решение:

По определению, удельная теплоемкость

(7.1)

Для смеси газов: 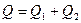, , где Q₁ и Q₂ – количество теплоты, получаемое аргоном и азотом соответственно; m₁ и m₂ массы компонентов смеси соответственно.

При P = const:

(7.2)

; (7.3)

- для аргона; - для азота

- для аргона; - для азота

При V = const:

(7.4)

 

; (7.5)

Для смеси газов:

 

при p = const или

 

или

 

 

Т.к. ; , то

 

( 7.6 )

Аналогично, при V = const:

( 7.7 )

Выражения (7.6) и (7.7) являются расчетными формулами для искомых величин:

 

 

 

Ответ: ; .

 

 

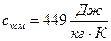Пример 8.В цилиндре под поршнем находится водород массой m = 0,02 кг при температуре . Водород начал расширяться адиабатно, увеличив свой объем в 5 раз, затем был сжат изотермически до первоначального объема. Найти температуру в конце адиабатного расширения и работу А, совершенную газом. Изобразить диаграмму процесса в P-V-координатах.

 

Решение:

Диаграмму процесса изобразим графически (рис. 9.1).

Адиабатный процесс 1-2 можно описать уравнением

(8.1)

где - показатель адиабаты, для 2-х атомного водорода i = 5; . Из (8.1) (8.2)

и т.к. по условию задачи , то

Работа газа при адиабатном расширении совершается за счет уменьшения внутренней энергии:

Работа при изотермическом сжатии на участке 2-3 равна:

.

Полная работа равна сумме и :

(8.3)

Для водорода .

Вычислим А, подставляя в (8.3) численные значения величин:

Ответ: ; А = 8,4 кДж.

 

Пример 9.В цилиндре двигателя внутреннего сгорания при работе образуются газы, температура которых . Температура отработанного газа . Двигатель расходует в час m = 36 кг топлива, теплота сгорания которого . Какую максимальную полезную мощность может развить этот двигатель?

 

Решение: Максимальная полезная мощность N_max может быть развита двигателем, если он работает с максимальным коэффициентом полезного действия . Для двигателя внутреннего сгорания к.п.д. максимален, если он работает по циклу Карно. Тогда:

. (9.1)

С другой стороны, по определению

, (9.2)

где: А - полезная работа; - тепло, полученное от нагревателя, в данном случае – от сгорающего топлива, т.е. . Поэтому

. (9.3)

Мощность двигателя: - работа А, совершаемая в единицу времени.

Выразив из (9.3) полезную работу А с учетом (9.1), получим максимальную полезную мощность:

. (9.4)

Здесь t = 1 ч = 3600 с – время сгорания топлива массой m = 3 6 кг.

Выражение (9.4) является расчетной формулой для искомой величины:

.

Ответ: N_max = 0,26 МВт.

 

Пример 10.Найти изменение энтропии при изобарном нагревании 10 г кислорода от до .

 

Решение:

По определению, изменение энтропии ,

где dQ – количество теплоты, получаемое термодинамической системой.

При изобарном нагревании

(10.1)

Поэтому:

, (10.2)

где μ = 32 · 10^-3 кг/моль – молярная масса кислорода; i = 5 – число степеней свободы молекулы кислорода, Т₁ = 273 + 50 = 323 К, Т₂ = 273 + 150 = 423 К.

Подставив численные значения, получим:

Ответ: .

Пример 11.Алюминий массой 561 г, нагретый до , погрузили в 400 г воды при . При этом часть воды испарилась, а оставшаяся приобрела температуру . Определить изменение энтропии системы.

 

Решение:

Изменение энтропии термодинамической системы определяется суммарным изменением энтропии тел, входящих в систему:

(11.1)

По определению

(11.2)

В данной задаче термодинамическую систему составляют алюминий и вода, причем, более нагретый алюминий отдает количество теплоты Q₁ воде и остывает до установившейся температуры теплового равновесия Т_об . Количество теплоты Q₁ расходуется на испарение части воды и нагрев оставшейся воды до установившейся температуры Т_об. Таким образом, для данной системы уравнение теплового баланса можно записать в виде: - Q₁ = Q₂ ,

где Q₂ – количество теплоты, получаемое водой, или

, (11.3)

где m_Al – масса алюминия; 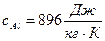- удельная теплоемкость алюминия; Т_Al – первоначальная температура алюминия; m_п – масса испарившейся воды; - удельная теплота парообразования воды; (m_в – m_п) – масса оставшейся воды; - удельная теплоемкость воды; Т_в - первоначальная температура воды; Т_об – установившаяся температура теплового равновесия термодинамической системы, Т_об = 273 + 50 = 323 К.

Уравнение (11.3) позволяет определить массу испарившейся воды m_п:

. (11.4)

Подставляя численные значения величин в (11.4), получим:

m_п = 0,0088 кг = 8,8 г. (11.5)

Так как в данной системе происходит остывание алюминия, параобразование и нагрев воды, то изменение энтропии этой системы по (11.1) определяется следующим образом:

, (11.6)

где - изменение энтропии при остывании алюминия до Т_об; - изменение энтропии при парообразовании (Т_п = const = 373 К); - изменение энтропии оставшейся части воды, нагревшейся до Т_об.

С учетом (11.2): , (11.7)

, (11.8)

. (11.9)

Подставляя в (11.6) выражения (11.7), (11.8), (11.9) и учитывая в системе СИ численные значения всех величин, вычислим изменение энтропии данной термодинамической системы:

Ответ: .

Пример 12. На какой глубине h под водой находится пузырек воздуха, если известно, что плотность воздуха в нем . Диаметр пузырька d = 15 мкм, температура t = 20^о С, атмосферное давление

Решение:

Давление внутри пузырька обусловлено состоянием воздуха в нем:

, или , (12.1)

где μ = 29 · 10^-3 кг/моль – молярная масса воздуха.

С другой стороны, это давление обусловлено давлением атмосферы Р₀, давлением столба воды над пузырьком Р₁ и добавочным давлением ΔР, созданным силами поверхностного натяжения под искривленной поверхностью:

, (12.1 а)

, (12.1 б)

где - плотность воды; h – высота столба (рис. 9.2), ( – коэффициент поверхностного натяжения воды). Таким образом

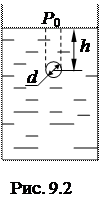
. (12.2)

 

Сравнивая (12.1) и (12.2) и решая уравнение относительно h, получим:

(12.3)

 

 

Вычисляем:

 

 

Ответ: h = 4,8 м.

 

 

Литература

 

1. Трофимова Т.И.: Курс физики. Учебное пособие для вузов. 7-е изд., - М.: Высшая шк., 2003 г.

2. Трофимова Т.И.: Физика в таблицах и формулах: Учебное пособие для студентов Вузов. – М.: Дрофа, 2002.

3. Трофимова Т.И., Павлова З.С.. Сборник задач по курсу физики с решениями: Учебн. пособие для вузов. 2-е изд., испр. М.: Высш. шк., 2001 г.

4. Волькенштейн В.С. Сборник задач по общему курсу физики. – Изд. 3-е, испр. и доп. – СПб.: Книжный мир, 2003.

5. Чертов А.Г., Воробьев А.А. Задачник по физики: Учеб. пособие. – 4-е изд., перераб. и доп. – М.: Высш. школа, 1981.

Матанцева Вера Анатольевна

Притыченко Лидия Митрофановна

 

 

 

Молекулярная физика и

Термодинамика

 

Сборник методических указаний

для самостоятельной работы студентов БГИТА

дневного и заочного обучения

 

Формат_____ Объем_______ Тираж______ Заказ _______ Бесплатно _______

 

Брянская государственная инженерно-технологическая академия

Брянская, проспект Станке Димитрова, 3, БГИТА

Редакционно-издательский отдел

 

 

Отпечатано – печатный цех БГИТА