 |
Главная |
Примеры заданий с решениями по теме. Задание №1. Пространство в цилиндре под поршнем, имеющее объем л
|
из
5.00
|
Задание №1. Пространство в цилиндре под поршнем, имеющее объем 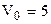 л, занимает один насыщенный водяной пар, температура которого
л, занимает один насыщенный водяной пар, температура которого  . Найти массу жидкой фазы, образовавшейся в результате изотермического уменьшения объема под поршнем до
. Найти массу жидкой фазы, образовавшейся в результате изотермического уменьшения объема под поршнем до  л. Насыщенный пар считать идеальным газом.
л. Насыщенный пар считать идеальным газом.
Решение:
Так как насыщенный пар по условию задачи можно считать идеальным газом, то для его начального и конечного состояния можно записать соответствующие уравнения состояния идеального газа. При этом нужно учесть, что при изотермическом уменьшении объема, давление остается прежним, а объем уменьшается из-за конденсации некоторой части пара (то есть превращения пара в жидкость).
 (1)
(1)
 (2)
(2)
Разделим правую и левую части уравнения (1) на соответствующие части уравнения (2) и получим:
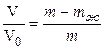 (3)
(3)
 (4)
(4)
Отсюда выразим искомую массу образовавшейся жидкости:
 (5)
(5)
Начальную массу пара  можно выразит из уравнения состояния (1):
можно выразит из уравнения состояния (1):
 (6)
(6)
Подставляя (6) в (5), находим окончательный результат:
 (7)
(7)
Используя исходные данные из условия задачи (  - нормальное атмосферное давление равное 105 Па, а
- нормальное атмосферное давление равное 105 Па, а  - молярная масса воды), получаем численное значение для массы сконденсированной жидкости:
- молярная масса воды), получаем численное значение для массы сконденсированной жидкости:
 г
г
Ответ: 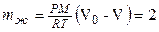 г.
г.
Задание №2. Вода массой 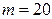 г находится при температуре 0 0С в теплоизолированном вертикальном цилиндре под невесомым поршнем, площадь которого
г находится при температуре 0 0С в теплоизолированном вертикальном цилиндре под невесомым поршнем, площадь которого 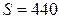 м2. Внешнее давление равно нормальному атмосферному. На какую высоту поднимется поршень, если воде сообщить количество тепла
м2. Внешнее давление равно нормальному атмосферному. На какую высоту поднимется поршень, если воде сообщить количество тепла 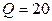 кДж.
кДж.
Решение:
Поршень начнет подниматься за счет превращения ее в насыщенный пар при увеличении температуры воды. Причем затраченное тепло пойдет не только на ее нагревание, но и на превращение воды в насыщенный пар.
Уравнение состояния насыщенного пара можно задать с помощью уравнения идеального газа:
 (1)
(1)
где 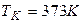 - температура кипения воды,
- температура кипения воды, 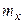 - масса пара, а
- масса пара, а  - объем цилиндра в конечном состоянии.
- объем цилиндра в конечном состоянии.
Полное количество теплоты можно представить в виде:
 (2)
(2)
где 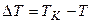 есть разность температуры кипения воды и начальной ее температуры, которая дана в условии задачи,
есть разность температуры кипения воды и начальной ее температуры, которая дана в условии задачи, 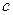 - удельная теплоемкость воды.
- удельная теплоемкость воды.
В формуле (2) первое слагаемое есть теплота парообразования, а второе – связано с простым нагреванием жидкости без изменения ее фазового состояния.
Теплота парообразования определяется соотношением:
 (3)
(3)
где  - удельная теплота парообразования для воды, значение которой можно определить в таблице
- удельная теплота парообразования для воды, значение которой можно определить в таблице
Из формулы (3) можно выразить массу пара и подставить ее в (1). В результате получим:
 (4)
(4)
Выразим теплоту парообразования в соотношении (2) и подставим в (4). В результате получим:
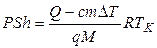 (5)
(5)
Используя соотношение (5) найдем высоту  , на которую поднимется поршень:
, на которую поднимется поршень:
 (6)
(6)
Подставляя данные задачи и справочные величины, определяем численное значение искомой величины:
 см.
см.
Ответ:  см.
см.
Задание №3. Лед, находившийся при нормальных условиях, подвергли сжатию до давления  атм. Считая, что понижение температуры льда в этих условиях линейно зависит от давления, найти какая часть льда растаяла. Удельный объем воды на
атм. Считая, что понижение температуры льда в этих условиях линейно зависит от давления, найти какая часть льда растаяла. Удельный объем воды на  см3/г меньше удельного объема льда.
см3/г меньше удельного объема льда.
Решение:
Для решения данной задачи воспользуемся уравнением Клапейрона – Клаузиуса, учитывая что при линейной зависимости  . Следовательно, производную можно заменить на приращения соответствующих величин.
. Следовательно, производную можно заменить на приращения соответствующих величин.
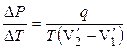 (1)
(1)
где:
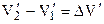 (2)
(2)
 (3)
(3)
Соотношение (2) соответствует разности удельных объемов льда и воды. Формула (3) характеризует разность давлений в конечном и начальном состоянии, а  - разность температур плавления при различных значениях.
- разность температур плавления при различных значениях.
При сжатии выделяется количество теплоты, идущее на плавление льда. Поэтому должен иметь место соответствующий тепловой баланс:
 (4)
(4)
где  - начальная масса льда, а
- начальная масса льда, а  - масса расплавленного льда.
- масса расплавленного льда.
Из соотношения (4) можно найти ту часть льда, которая растает. Она будет равна отношению массы расплавленного льда к его начальной массе:
 (5)
(5)
Из уравнения Клапейрона – Клаузиуса выразим  :
:
 (6)
(6)
Подставим (6) в (5) и получим:
 (7)
(7)
Так как давление после сжатия намного больше начального (нормального атмосферного давления), то величиной второго можно в (3) и соответственно в (7) пренебречь:
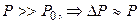 (8)
(8)
Учитывая (8) для искомой величины окончательно получаем:

Подставляя значения заданных и соответствующих табличных величин, находим численной значение искомой величины:

Ответ: 
|
из
5.00
|
Обсуждение в статье: Примеры заданий с решениями по теме. Задание №1. Пространство в цилиндре под поршнем, имеющее объем л |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

