Примеры заданий с решениями по теме. Задание №1. Во сколько раз надо расширить адиабатически газ

Задание №1. Во сколько раз надо расширить адиабатически газ, состоящий из жестких двухатомных молекул, чтобы их средняя квадратичная скорость уменьшилась в раза.

Решение:

Из распределения Максвелла следует, что средняя квадратичная скорость молекул зависит от температуры газа. Поэтому уравнение адиабаты следует рассматривать относительно плоскости (T,V) для двух заданных состояний:

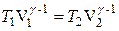(1)

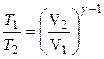(2)

Среднеквадратичная скорость молекул связана с температурой газа по формуле:

(3)

По условию средняя квадратичная скорость в процессе расширения уменьшилась в раз:

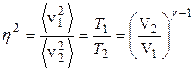(4)

Искомое отношение объемов обозначим как:

(5)

Преобразуем (4) с учетом (5):

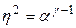(6)

Выразим из соотношения (6) и получим искомую величину (во сколько раз расширится газ при адиабатическом процессе):

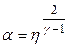(7)

Величина в (7) является коэффициентом Пуассона, который связан с числом степеней свободы газа 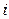по формуле:

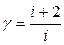(8)

Показатель степени в (7) преобразуем с помощью соотношения (8):

(9)

Подставляя (9) в (7), получаем:

(10)

Число степеней свободы двухатомного газа с жесткой связью молекул равна пяти и учитывает только три поступательные степени и две вращательные. Находим , используя данные задачи:

раза.

Ответ: В 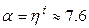раза расширится газ.

Задание №2. Смесь водорода и гелия находится при температуре К. При каком значении скорости 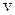молекул значения функций распределения Максвелла будут одинаковыми для обоих газов.

Решение:

Запишем функции распределения Максвелла для каждого элемента смеси, учитывая условие задачи о равенстве температур, а, следовательно, и скоростей молекул элементов смесей. При этом их молярные массы различны.

(1)

где - номер элемента смеси.

Масса молекулы связана с молярной массой по формуле:

(2)

Подставляя (2) в (1), получаем:

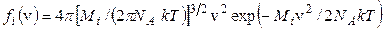(3)

По условию задачи функции распределения должны быть одинаковыми:

(4)

Подставляя (3) в (4), находим:

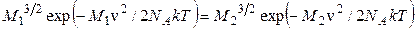(4)

Отсюда:

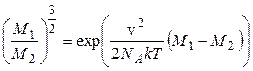(6)

Возьмем натуральный логарифм от обеих частей соотношения (6):

(7)

где 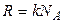- универсальная газовая постоянная

Выразим из (7) искомую скорость:

(8)

Подставляя значения молярных масс элементов смеси из таблицы Менделеева и температуру, находим численное значение скорости:

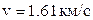
Ответ: .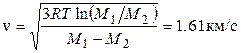

Задание №3. Потенциальная энергия молекул газа в некотором центральном поле зависит от расстояния 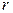до центра поля как , где - положительная постоянная. Температура газа , концентрация молекул в центре поля 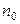. Найти: 1) число молекул, находящихся в интервале расстояний ; 2) наиболее вероятное расстояние молекул от центра поля; 3) относительное число всех молекул в слое .

Решение:

Для решения задачи используем распределение Больцмана, задающее число молекул, находящихся в интервале расстояний , для поля потенциальных сил:

(1)

В нашем случае они являются центральными, поэтому удобно перейти от пространственной декартовой системы координат к сферической, учитывая, что потенциальная энергия не зависит от углов этой системы:

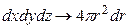(2)

Подставляя замену (2) и выражение для потенциальной энергии рассматриваемого поля в (1), получаем:

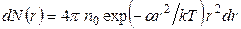(3)

где 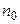заданная концентрация в центре рассматриваемого поля.

Плотность вероятности этого распределения определяется из сравнения (3) со следующим математическим определением:

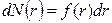(4)

(5)

Наиболее вероятное расстояние молекул от центра поля может быть найдено из условия экстремума этой функции:

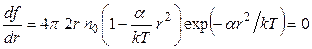(6)

Так в нуль может обращаться только выражение в скобках, получаем искомое значение:

(7)

Для того, чтобы найти относительное число всех молекул в слое , необходимо найти полное число молекул в пространстве и выразить отношение: , где 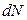определяется соотношением (3) данной задачи.

Полное число молекул для данного распределения можно рассчитать, проинтегрировав (3):

(8)

Возьмем отдельно данный интеграл, сделав замену , :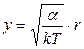

(9)

Интеграл в (9) табличный и равен:

(10)

Подставляя (10) в (9), а затем (9) в (8), получаем:

(11)

Далее находим относительное число всех молекул в слое как отношение , разделив (3) на (10):

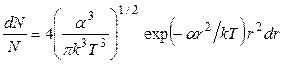(12).

Ответ: 1) 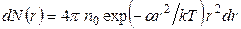; 2) ; 3) .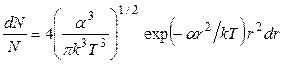

Фазовые превращения