 |
Главная |
Примеры заданий с решениями по теме. Задание №1. В результате некоторого процесса вязкость идеального газа увеличилась в
|
из
5.00
|
Задание №1. В результате некоторого процесса вязкость идеального газа увеличилась в 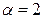 раза, а коэффициент диффузии – в
раза, а коэффициент диффузии – в  раза. Как и во сколько раз изменилось давление газа.
раза. Как и во сколько раз изменилось давление газа.
Решение:
Воспользуемся соотношениями, которые являются математическими определениями для коэффициентов диффузии и вязкости:
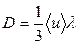 (1)
(1)
 (2)
(2)
Плотность идеального газа выражается через давление и температуру с помощью его уравнения состояния:
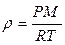 (3)
(3)
Средняя скорость молекул идеального газа связана с температурой соотношением:
 (4)
(4)
Длина свободного пробега выражается через концентрацию молекул, а значит и через давление  :
:
 (5)
(5)
где  эффективное сечение молекулы, значение которого слабо зависит от давления и температуры
эффективное сечение молекулы, значение которого слабо зависит от давления и температуры
Подставим (3) – (5) в соотношения (1) и (2) и получим:
 (6)
(6)
 (7)
(7)
Из (6) и (7) видно, что коэффициент диффузии зависит как от температуры, так и от давления, а коэффициент вязкости только от температуры. Используя эти формулы, установим связь между  и
и  :
:
 (8)
(8)
Формула в верна как для конечного, так и для начального состояния, причем изменяться в ней будут только величины  ,
,  и
и  :
:
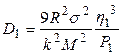 (9.1)
(9.1)
 (9.2)
(9.2)
Разделим (9.2) на (9.1) и получим:
 (10)
(10)
По условию  , а
, а  , следовательно (10) примет вид:
, следовательно (10) примет вид:
 (11)
(11)
Из (11) можно найти как изменилось давление:
 (12)
(12)
Ответ:В результате данного процесса давление увеличилось в 2 раза.
Задание №2. Найти показатель политропы  процесса, совершаемого идеальным газом, при котором остается неизменным 1) коэффициент диффузии; 2) вязкость, 3) теплопроводность.
процесса, совершаемого идеальным газом, при котором остается неизменным 1) коэффициент диффузии; 2) вязкость, 3) теплопроводность.
Решение:
Используем соотношение (6) из прошлой задачи для коэффициента диффузии:
 (1)
(1)
Удовлетворим условию 1) о неизменности коэффициента диффузии для двух произвольных состояний и подставим правую часть (1):
 (2)
(2)
 (3)
(3)
Используя уравнение состояния идеального газа переедем в (3) на плоскость  :
:
 (4)
(4)
 (5)
(5)
Так как уравнение политропы на соответствующей плоскости в общем случае имеет вид:
 (6)
(6)
то показатель политропы  можно найти из уравнения для показателя степени, полученного из сравнения (5) с (6):
можно найти из уравнения для показателя степени, полученного из сравнения (5) с (6):

Далее используем соотношение (7) из прошлой задачи для коэффициента вязкости:
 (7)
(7)
При условии, что коэффициенты вязкости в двух различных состояниях одинаковы, следует равенство и их температур (то есть рассматриваемый процесс изотермический):
 (8)
(8)
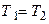 (9)
(9)
Уравнения изотермы на плоскости  и политропы имеют соответствующий вид:
и политропы имеют соответствующий вид:
 (10)
(10)
 (11)
(11)
Сравнивая (10) с (11) находим, что:

Зависимость коэффициента теплопроводности от параметров  и
и  такая же, как и для коэффициента вязкости (
такая же, как и для коэффициента вязкости (  - в формуле для коэффициента теплопроводности не зависит от данных параметров, а только от степени свободы и молярной массы данного газа). Следовательно, при равенстве соответствующих коэффициентов
- в формуле для коэффициента теплопроводности не зависит от данных параметров, а только от степени свободы и молярной массы данного газа). Следовательно, при равенстве соответствующих коэффициентов  , температуры также одинаковы
, температуры также одинаковы 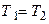 и показатель политропы равен единице (
и показатель политропы равен единице (  )
)
Ответ: 1)  ; 2)
; 2)  , 3)
, 3)  .
.
Задание №3. Найти распределение температур в веществе, находящимся между двумя большими параллельными пластинами, если последние поддерживают при температурах  и
и  , расстояние между ними равно
, расстояние между ними равно  и теплопроводность вещества
и теплопроводность вещества  .
.
Решение:

Рис. 4.
Воспользуемся уравнением теплопроводности для потока тепла:
 (1)
(1)
где ось OX перпендикулярна пластинам
Решим дифференциальное уравнение (1) в рассматриваемом интервале температур от  до
до  при заданной теплопроводности вещества. Определим с помощью него неизвестные величины:
при заданной теплопроводности вещества. Определим с помощью него неизвестные величины:
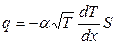 (2)
(2)
где  - некоторый коэффициент пропорциональности
- некоторый коэффициент пропорциональности
 (3)
(3)
 (4)
(4)
 (5)
(5)
Из соотношения (5) можно выразит неизвестные величины в задаче:
 (6)
(6)
Проведем мысленно параллельную плоскость на малом расстоянии 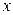 от пластины с температурой
от пластины с температурой  . Температура на этой произвольно выбранной параллельной плоскости будет соответствовать искомой
. Температура на этой произвольно выбранной параллельной плоскости будет соответствовать искомой  (см. рис. ). Тогда при решении уравнения (3) необходимо использовать новые пределы интегрирования. Для температуры верхний предел будет равен
(см. рис. ). Тогда при решении уравнения (3) необходимо использовать новые пределы интегрирования. Для температуры верхний предел будет равен  , а для расстояния вдоль оси OX верхний предел будет равен
, а для расстояния вдоль оси OX верхний предел будет равен 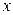 . В результате соответствующих изменений получим:
. В результате соответствующих изменений получим:
 (7)
(7)
Уравнение (7) даст решения вида (6):
 (8)
(8)
Сравнивая соотношения (6) и (8), делаем заключение о равенстве их правых частей. Из этого равенство следует уравнение из которого затем можно выразить температуру как функцию от расстояния между пластинами  .
.
 (9)
(9)
 (10)
(10)
Ответ: 
Варианты тестов итогового контроля по разделу:
Молекулярная физика
ТЕСТ№1
1. Какие подходы используются для описания процессов и явлений в молекулярной физике?
2. В чем состоит суть термодинамического подхода?
3. Какой процесс называется обратимым?
4. Меру нагретости тела характеризует ________.
5. Основными термодинамическими параметрами являются:
6. Уравнение состояния идеального газа имеет вид ________.
7. Процесс, который происходит при постоянной температуре и массе вещества называется ________.
8. В случае адиабатического процесса газ охлаждаясь _________ (указать, что происходит с его объемом).
9. Уравнение адиабаты на плоскости P,V имеет вид ________.
10. Запишите уравнение Майера.
11. Чему равен показатель политропы.
12. Какие из перечисленных функций являются функциями состояния: термодинамическая работа, теплота, внутренняя энергия, энтропия, энтальпия, свободная энергия?
13. Что представляет собой внутренняя энергия газа? Функцией чего она является?
14. При каком процессе термодинамическая работа равна нулю?
15. Каков физический смысл энтропии с точки зрения термодинамического подхода? Чему она равна?
16. Фазовыми переходами первого рода называют _________.
17. Записать уравнение Клайперона - Клаузиуса.
18. Критической температурой называют такое ее значение, при котором вещество __________.
19. Что является общей чертой всех явлений переноса
20. Что называют диффузией? Приведите уравнение Фика (диффузии).
ТЕСТ№2
1. В чем состоит суть статистического подхода?
2. Какой процесс называется необратимым?
3. Записать основное уравнение МКТ.
4. Процесс, который происходит при постоянной массе и объеме вещества называется ________.
5. Все процессы, которые происходят с постоянной теплоемкостью, называют _________.
6. Чему равен коэффициент Пуассона.? (через молярные теплоемкости).
7. В чем заключается физический смысл универсальной газовой постоянной?
8. Выражение для термодинамической работы в дифференциальной форме имеет вид ________.
9. Уравнение адиабаты на плоскости T,V имеет вид ________.
10. Какие из перечисленных функций являются функциями процесса: термодинамическая работа, теплота, внутренняя энергия, энтропия, энтальпия, свободная энергия?
11. Функцией какого параметра является термодинамическая работа?
12. Возможен ли теплообмен при постоянной энтропии системы? (Поясните).
13. Каков физический смысл энтропии с точки зрения статистического подхода? Чему она равна?
14. Фазовыми переходами второго рода называют _________.
15. Уравнение Ван-дер-Ваальса для одного моля вещества имеет вид _________.
16. С ростом высоты над уровнем моря атмосферное давление _________. (Дать ответ и привести барометрическую формулу)
17. Чему равно значение наиболее вероятной скорости молекул?
18. Записать в общей форме классическое распределение Максвелла – Больцмана.
19. Записать уравнение Ньютона для коэффициента вязкости.
20. Что называют теплопроводностью? Записать уравнение Фурье (теплопроводности).
Примеры контрольных работ с ответами по разделу:
Молекулярная физика.
Вариант I
1. В сосуде находится смесь  азота и
азота и  углекислого газа при температуре
углекислого газа при температуре 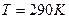 и давлении
и давлении  . Найти плотность этой смеси, считая газ идеальным. (Ответ:
. Найти плотность этой смеси, считая газ идеальным. (Ответ:  г/л)
г/л)
2. Один моль идеального газа, теплоемкость которого при постоянном давлении  , совершает процесс по закону:
, совершает процесс по закону:  . Найти теплоемкость газа как функцию от его объема; сообщенное газу тепло при его расширении от
. Найти теплоемкость газа как функцию от его объема; сообщенное газу тепло при его расширении от  до
до  . (Ответ:
. (Ответ:  )
)
3. У тепловой машины, работающей по циклу Карно, температура нагревателя в  раза больше температуры холодильника. За один цикл машина производит работу
раза больше температуры холодильника. За один цикл машина производит работу  кДж. Какая работа за цикл затрачивается на изотермическое сжатие рабочего вещества? (Ответ:
кДж. Какая работа за цикл затрачивается на изотермическое сжатие рабочего вещества? (Ответ:  кДж)
кДж)
Вариант II
1. В баллоне, объемом  при температуре
при температуре  находится смесь идеальных газов:
находится смесь идеальных газов:  кислорода,
кислорода,  азота и
азота и  углекислого газа. Считать газы идеальными. Найти молярную массу смеси. (Ответ:
углекислого газа. Считать газы идеальными. Найти молярную массу смеси. (Ответ:  г/моль)
г/моль)
2. Во сколько раз следует увеличить изотермически объем идеального газа в количестве 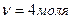 , чтобы его энтропия испытала приращение
, чтобы его энтропия испытала приращение 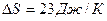 ? (Ответ: в
? (Ответ: в  раза)
раза)
3. В каком случае КПД цикла Карно повысится больше: при увеличении температуры нагревателя на  или при уменьшении температуры холодильника на такую же величину? (Ответ: во втором случае)
или при уменьшении температуры холодильника на такую же величину? (Ответ: во втором случае)
Вариант III
1. В идеальной тепловой машине абсолютная температура нагревателя в два раза больше абсолютной температуры холодильника. Если за один цикл холодильнику было передано количество теплоты  Дж, то, какое нагреватель передал газу количество теплоты? (Ответ:
Дж, то, какое нагреватель передал газу количество теплоты? (Ответ: 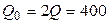 Дж)
Дж)
2. Имеется идеальный газ, молярная теплоемкость которого  известна. Найти молярную теплоемкость этого газа как функцию его объема
известна. Найти молярную теплоемкость этого газа как функцию его объема  , если газ совершает процесс по закону:
, если газ совершает процесс по закону:  . (Ответ:
. (Ответ:  )
)
3. Как изменится коэффициент диффузии  и вязкость
и вязкость  идеального газа, если его объем увеличить в
идеального газа, если его объем увеличить в  раз изотермически? (Ответ:
раз изотермически? (Ответ:  увеличится в
увеличится в  раз,
раз, 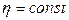 )
)
Вариант IV
1. При очень низких температурах теплоемкость кристаллов  , где
, где  , Найти энтропию как функцию температуры в этой области. (Ответ:
, Найти энтропию как функцию температуры в этой области. (Ответ:  )
)
2. Найти уравнение процесса в переменных T,V при котором молярная теплоемкость идеального газа изменяется по закону:  . (Ответ:
. (Ответ:  )
)
3. Как изменится коэффициент диффузии  и вязкость
и вязкость  идеального газа, если его объем увеличить в
идеального газа, если его объем увеличить в  раз изобарически? (Ответ:
раз изобарически? (Ответ:  увеличится в
увеличится в  раз,
раз,  - в
- в  раз)
раз)
Приложение 1
Таблица 1.
|
из
5.00
|
Обсуждение в статье: Примеры заданий с решениями по теме. Задание №1. В результате некоторого процесса вязкость идеального газа увеличилась в |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

