Примеры заданий с решениями по теме

Задание №1. В сосуде объемом л содержится идеальный газ при температуре 0 ⁰С. После того как часть газа была выпущена наружу давление понизилось на атм. (без изменения температуры). Найти массу выпущенного газа. Плотность данного газа при нормальных условиях г/л.

Решение:

Рис. 1.

По условию задачи процесс происходит при постоянной температуре и с неизменным объемом: , .

Однако масса газа, после того как он был выпущен из сосуда уменьшается на , а, следовательно, и падает давление в сосуде на , которое известно по условию.

Так как рассматриваемый газ можно считать идеальным, то для его начального состояния и конечного состояния (после того как газ был выпущен) можно записать соответствующие уравнения идеального газа.

Для начального состояния:

(1)

Для конечного состояния:

(2)

где Па – давление газа при нормальных условиях равное атмосферному.

Перенесем в уравнениях (1) и (2) неизменные величины в правую часть, а изменяющиеся в левую часть:

(3)

(4)

Так как правые части (3) и (4) равны, то должны быть равны и левые части:

(5)

Из соотношения (5) находим :

(6)

(7)

(8)

где массу газа в начальном состоянии, которое имело место при нормальных условиях можно представить в виде:

(9)

Подставляя (9) в (8) получаем окончательный результат:

(10)

г.

Ответ:

Задание №2. Уравнения процессов имеют вид: 1) ; 2) , где - положительные постоянные, - объем моля газа. Найти максимально возможную температуру идеального газа в каждом указанном процессе.

Решение:

Перейдем в заданных уравнениях процессов от давления к температуре с помощью уравнения состояния идеального газа для одного моля, в соответствие с требованием задачи.

(1)

Подставим (1) в уравнения процессов, выражая температуру как функцию от объема:

(2)

(3)

Чтобы получить экстремальное (максимальное) значение какой либо функции, необходимо найти её производную по имеющемуся аргументу и приравнять к нулю. Из полученного уравнения определить соответствующее значение аргумента и подставить его в выражение для функции. В нашем случае температура является функцией, а объем ее аргументом. Поэтому возьмем от (2) и (3) производную по :

(4)

(5)

Корнями уравнений (4) и (5) являются следующие значения объема:

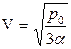(6)

(7)

Подставляя (6) и (7) в (2) и (3) соответственно, получаем:

(8)

(9)

Ответ: 1) ; 2) .

Задание №3. Высокий цилиндрический сосуд с азотом находится в однородном поле тяжести Земли. Температура азота меняется так, что его плотность повсюду одинакова. Найти градиент температуры .

Решение:

Рис. 3.

Рассмотрим бесконечно тонкий слой азота, толщиной , параллельный основанию цилиндрического сосуда. Его масса:

(1)

В однородном поле силы тяжести на него действует сила:

(2)

С другой стороны рассматриваемый слой создает давление , которому соответствует сила (она равна по модулю силе тяжести):

(3)

(4)

Подставляя в (3) соотношения (1), (2), (4), получаем:

(5)

Знак минус в (5) указывает, что давление убывает с ростом высоты.

В соответствии с уравнением состояния идеального газа:

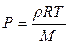(6)

Так как по условию плотность – постоянная величина, то бесконечно малое изменение давления приводит согласно (6) к бесконечно малому изменению температуры:

(7)

Подставляя (7) в (5), получаем:

(8)

Из соотношения (8), находим градиент температуры:

(9)

Ответ: .