Обоснование основных соотношений и исходных данных

 

Для повышения безопасности территории (страны, региона, субъекта федерации, города) в условиях возможной реализации природных и техногенных опасностей необходимо принимать превентивные меры защиты, направленные на а) предотвращение стихийных бедствий и б) смягчение их последствий. Их осуществление требует затрат, размер которых зависит от вида опасности, числа защищаемых объектов инфраструктуры и других факторов. В условиях ограниченных ресурсов выбор мер защиты и защищаемых объектов должен быть рациональным. Естественно, что достижение этого без подходящего математического аппарата потребует жизненного опыта многих поколений.

Общие подходы к оптимальному управлению рисками, обеспечению безопасности населения и окружающей среды изложены в ряде работ. Известно огромное число работ по приложениям методов оптимизации к решению различных задач. Однако конкретные постановки задач оптимизации защиты территории в известных работах исследованы недостаточно, отсутствуют методики оптимизации, адаптированные к имеющимся исходным данным, содержащимся, например, в паспортах безопасности субъектов РФ.

Распределение ресурсов территорий на снижение рисков и смягчение последствий ЧС целесообразно проводить с помощью двухэтапной процедуры. На первом этапе определяются доли ресурсов на защиту территории по видам опасностей, а на втором выбираются конкретные защищаемые объекты инфраструктуры из числа уязвимых по отношению к рассматриваемой опасности объектов.

Вероятности катастроф на потенциально опасных объектах, повторяемость различных опасных природных явлений и уязвимость элементов инфраструктуры по отношению к их поражающим факторам, а, следовательно, и необходимые финансовые затраты на защиту различаются. Учитывая, что затраты на защиту ограничены экономическими возможностями рассматриваемой территории, сформулируем задачу рационального распределения ресурсов на защиту при наличии ограничений.

Без ограничения общности рассмотрим задачу распределения ресурсов территории на снижение рисков и смягчение последствий стихийных бедствий по видам инициирующих их опасных природных явлений.

Пусть территория включает объекты инфраструктуры (опасные производственные объекты, объекты жизнеобеспечения, жилые и промышленные здания и сооружения, гидротехнические сооружения, транспортные коммуникации и их элементы, трубопроводы, инженерные сооружения защиты от опасных природных явлений и др.), при разрушении которых из-за формирования вторичных поражающих факторов опасное природное явление перерастает в стихийное бедствие. Опасность территории с точки зрения возможности возникновения ЧС характеризуется m источниками опасности со среднемноголетними частотами реализации l_j = 1/T_j, где T_j (j=1,…,m) – повторяемость опасных природных явлений j-го вида (средний интервал времени, лет, между опасными природными явлениями). Данные о повторяемости опасных природных явлений в одном из субъектов РФ – Нижегородской области приведены в табл. 14 (получены по результатам специально проведенной научно-практической работы).

Сила U поражающих факторов, действующих на объекты инфраструктуры, по совокупности реализаций опасного природного явления и пространственного распределения очагов возникновения опасности по отношению к объектам воздействия является случайной величиной. Она описывается характерной для рассматриваемой территории и размещения объектов на ней (с учетом пространственного фактора ослабления силы поражающего фактора с удалением от возможного очага опасного природного явления) функцией распределения поражающих факторов, формируемых при реализации опасности, по силе F(u) = P(U<u). Эта функция может быть определена по данным многолетних наблюдений статистическими методами. Известны, например, функции распределения для городов РФ максимальной скорости ветра, силы землетрясений, уровней подъема воды в реках и др.

Случайную величину U_кр можно интерпретировать также как критическую силу, до которой еще не происходит разрушения. В этом случае она характеризует стойкость (например, сейсмостойкость) объекта, а ее вероятностным описанием является функция стойкости R_кр(u) = 1 - F_кр(u) = P(U_кр³u).

Если при попадании объекта в зону действия поражающих факторов опасного природного явления возможно его разрушение, то объект считается уязвимым. Условие (модель “нагрузка - прочность”) разрушения объекта поражающим фактором j-го опасного природного явления записывается в виде U_j > U_крj , а вероятность этого события –

q = P(U_j > U_крj) (23)

Величина произведения l_jq_j является характеристикой безусловной уязвимости объектов на рассматриваемой территории. Для каждой территории стихийно на основе жизненного опыта многих поколений, национальных особенностей, экономического положения и других факторов, учитывающих частоту опасных природных явлений и ущерб от вызываемых ими стихийных бедствий) устанавливается определенный уровень уязвимости. Управляемым параметром при этом является величина m_крj =M[U_крj], регламентируемая СНиП.

Так, если вероятность превышения действующей от опасного природного явления нагрузкой стойкости объектов составляет q_j =0,1, то при частоте опасных природных явлений l_j = 0,1 1/год (в среднем один раз в 10 лет) разрушение объектов будет происходить с частотой l_jq_j = 0,1´0,1=0,01 (раз в 100 лет).

Число N_j объектов инфраструктуры, подвергающихся угрозе разрушения поражающими факторами опасных природных явлений со значительными вторичными последствиями, т.е. уязвимых в настоящее время к этим воздействиям, для Нижегородской области приведено в табл. 14.

 

 

Таблица 14

Данные о повторяемости опасных природных явлений в Нижегородской области, ущербе от них и затратах на предотвращение (в скобках приведены данные, усредненные по субъектам РФ, входящим в Центральный регион)

Параметр	Вид опасного природного явления
Смерч	Ураган	Шкв. ветер	Опол-зень	Карст (провалы)	Навод-нения	Силь-ная засуха	Лесные пожары
Среднемноголетняя частота lj, 1/(область×лет) возникновения опасных природных явлений	0,14	0,5	5,0	0,3	0,7	1,0	0,03	1,0
Число объектов Nj, подвергающихся угрозе воздействия от j-го опасного природного явления							-
Средняя доля aпj уязвимых объектов от их общего числа, подвергающихся воздействию негативных факторов опасного природного явления в случае его реализации	0,01	0,02	0,01	0,01	0,1	0,06	-	0,15
Число nj разрушенных объектов в год	1,19			0,048	0,56		-	94,5
Средние затраты dgj на предотвращение стихийных бедствий, тыс. руб./объект	-	-	(10000)	- (700)	(900)	(10000)	- (2700)	(6200)
Средний материальный ущерб от одной ЧС, тыс. руб./бедствие			(33000)	(3000)	(300000)	(16000)	(107000)	(68000)

 

Для опасных природных явлений характерно распределение не только во времени, но и в пространстве (расположение очага, размер зоны действия его поражающих факторов). Не все объекты инфраструктуры на рассматриваемой территории в случае реализации опасного природного явления попадают в зону действия их негативных факторов. Доля

a_пj = ,

где S_пj – площадь зоны действия поражающих факторов в случае реализации j-й опасности, объектов, подвергающихся воздействию поражающих факторов в случае возникновения j-го опасного природного явления (угрозе разрушения), от их общего числа может быть определена расчетным или экспертным методом. Величина a_пj для Нижегородской области, определенная экспертным путем, приведена в табл. 14. С ее учетом математическое ожидание числа объектов инфраструктуры, подвергающихся угрозе разрушения от j-й опасности, составит a_пj N_j, а числа разрушенных объектов в расчете на год – n_j = a_j(Dt) a_пj q_j N_j.В табл. 14 приведены верхние оценки прогнозируемого числа разрушенных объектов в год в случае реализации опасных природных явлений в Нижегородской области (при условии, что q_j =1 "j).

Для снижения уязвимости объектов инфраструктуры осуществляются меры защиты, под которыми в общем случае понимают все меры по снижению риска ЧС. В зависимости от принятой стратегии повышения безопасности территории это:

упрочнение (усиление, укрепление) уязвимых объектов, направленное на предотвращение развития опасных природных явлений в стихийное бедствие. Согласно современным нормативам приемы, например, сейсмостойкого строительства удорожают стоимость городских зданий, рассчитанных на устойчивость при землетрясениях в 7, 8 и 9 баллов, на 2-4, 4-8 и 10-15 % соответственно;

инженерная защита населения и территорий. Как показывает опыт, мероприятия инженерной защиты обеспечивают снижение возможных людских и материальных потерь на 30-40 %, но требуют значительных затрат;

ликвидация (перепрофилирование) уязвимых потенциально опасных объектов;

смягчение последствий ЧС (создание, например, запасов материальных средств) и др.

Однако ни одна из мер не может в полной мере гарантировать безопасность населения, поэтому обычно используется комплекс мер.

Чем больше средняя сила поражающего фактора m=M[U] и средняя уязвимость m_кр= M[U_кр] объектов на рассматриваемой территории, тем значительнее должны быть меры защиты для исключения их разрушения. Необходимые объем мер защиты, обеспечивающих неразрушение объектов, и средние затраты d_gj на защиту одного объекта от j-й опасности рассчитывают с учетом соотношения силы поражающих факторов и уязвимости объектов инфраструктуры. Средние по совокупности разнородных объектов финансовые затраты d_gj на предотвращение разрушения уязвимых объектов в Нижегородской области и усредненные данные по субъектам федерации, входящим в Центральный регион, приведены в табл. 14.

Будем полагать, что в случае принятия мер защиты стойкость u_кр объекта к воздействию поражающих факторов опасного природного явления повышается (условная уязвимость снижается) настолько, что q ® 0. Обозначим через N_gj число защищенных от j-й опасности объектов из числа уязвимых. Тогда доля g_j = N_gj/N_j защищенных элементов инфраструктуры является показателем защищенности территории от j-й опасности. При сделанном допущении разрушение объектов инфраструктуры возможно только в случае отсутствия защиты. Представим совокупность объектов инфраструктуры как смесь двух выборок – незащищенных от j-й опасности объемом N_j - N_gj и защищенных объемом N_gj. Тогда оценка условной вероятности разрушения произвольного объекта инфраструктуры определится по формуле

q’_j = q_j , (24)

где = 1 – g_j – показатель уязвимости территории, а математическое ожидание числа разрушенных объектов при условии воздействия поражающих факторов опасного природного явления составит q_j N_j.

На суммарные затраты по повышению защищенности территории

С_g = c_gj g_j, (25)

где c_gj = d_gj N_j, наложено ограничение

С_g £ С_выд, (26)

где С_выд - выделенные ресурсы на защиту, которые складываются из доли ресурсов центра, определяемых по методике предыдущей главы, и собственных ресурсов, размер которых ограничивается экономическими возможностями территории.

Разрушение произвольного объекта инфраструктуры на рассматриваемой территории от поражающих факторов j-го опасного природного явления является сложным событием, которое наступает в случае совместной реализации следующих независимых событий:

1) реализации опасности j-го вида на рассматриваемой территории - характеризуется математическим ожиданием числа a_j реализаций опасных явлений;

2) попадания объектов инфраструктуры в зону действия поражающих факторов (пространственный фактор) – характеризуется долей a_пj объектов от их общего числа, подвергающихся угрозе разрушения в случае реализации опасности;

3) разрушения произвольных объектов из числа уязвимых, подвергшихся воздействию поражающих факторов от опасности j-го вида, при условии реализации программы защиты – характеризуется вероятностью q’_j, определяемой по формуле (24).

Полагая, что события воздействия поражающих факторов опасных природных явлений на объекты инфраструктуры в течение рассматриваемого интервала времени (года) являются редкими, можно предположить, что угрозе разрушения в случае реализации опасностей подвергаются различные объекты. Тогда математическое ожидание числа разрушенных объектов за рассматриваемый интервал времени определится по формуле

, (27)

где n_j = a_j a_пj q_j N_j - математическое ожидание числа разрушенных объектов за год в результате действия поражающих факторов j-го природного явления.

Пусть с_0j = с₀ " j – ущерб от разрушения одного объекта. Тогда ущерб от стихийного бедствия, инициированного j-м опасным природным явлением, вычисляется по формуле

C_ЧСj = с₀n_j.

Средний материальный ущерб от одного стихийного бедствия для Нижегородской области и в среднем по Центральному региону приведен в табл. 14.

Суммарный ущерб от ЧС природного характера определяется по формуле

C_ЧС = , (28)

где c_ЧСj = с₀ a_j a_ПФj q_j N_j.

Определим вначале рациональный план распределения имеющихся ресурсов на повышение защищенности территории по отношению к различным опасностям с учетом ограничения (26).

 

Выбор целевой функции

 

В качестве оптимизируемых параметров будем использовать показатели защищенности g_j (j=1,...,m), которыми при планировании мер защиты можно управлять. Обозначим их вектором g = (g₁,…,g_m)^т.

С экономической точки зрения наиболее общими целевыми функциями являются следующие:

1) сумма ущерба от ЧС C_ЧС и затрат на защиту С_g (или только ущерб от ЧС), с учетом (25) и (28) равная . Критерием оптимальности является минимум целевой функции. Исключив постоянную составляющую, представим целевую функцию в виде

f(g) = c’g, (29)

где c’ – вектор целевых коэффициентов с компонентами c’_j = c_gj - c_ЧСj j=1,…,m.

2) разность между предотвращенным ущербом C_ПУ и затратами на защиту С_g (или только предотвращенный ущерб) Критерием оптимальности является максимум целевой функции. Предотвращенный ущерб вычисляется по формуле

C_ПУ = C_ЧС0 - C_ЧС = c₀ (n₀ - n),

где C_ЧС0и n₀ – ущерб от природных ЧС и математическое ожидание числа разрушенных элементов без принятия мер защиты (при =1 "j).

С учетом (28) С_ПУ = 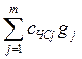. Тогда

f(g) = C_ПУ - C_g = , (30)

где c_j = c_ЧСj - c_gj .

Таким образом, рассмотренные целевые функции являются взаимно обратными.

3.3 Оптимизация защиты территории от различных

опасностей методом линейного программирования

(определение доли выделяемых средств)

 

Выберем целевую функцию и ограничения. Пусть N_j ® ¥, т.е. g_j может принимать любые значения на [0,1]. Тогда задача оптимизации формулируется в следующем виде:

f(g) =

£ С_выд, (31)

g_j £1,

g_j ³ 0 .

Представим ее как каноническую задачу линейного программирования:

f(g)= c g ® max

A g = b,

g ³ 0 ,

где g = (g₁,…, g_m)^т – искомый вектор, с = (c₁, ..., c_m) - вектор целевых коэффициентов,

A = - матрица условий порядка k´m,

b = (C_выд,1,...,1)^т - вектор ограничений (вектор-столбец порядка k).

Система линейных неравенств выделяет в m-мерном пространстве множество G тех векторов g = (g₁,…, g_m)^т, чьи координаты удовлетворяют этой системе (gÎG). Экстремум достигается в одной из крайних точек допустимого множества G. В силу двойственности задач линейного программирования задачи минимизации целевой функции (29) и максимизации целевой функции (30) дают одно и то же оптимальное решение.

Так как число защищаемых элементов инфраструктуры N_gj = g_j N_j принимает только целочисленные значения, то при конечных N_j показатели защищенности g_j принимают дискретные значения. Следовательно, решаемая задача относится к типу задач с неделимостями, для решения которых следует применять целочисленное программирование. Методы решения задачи целочисленного программирования (округления значений переменных, “отсечений”, “ветвей и границ”) основаны на использовании решения базовой задачи линейного программирования. Метод округления дает решение, которое хуже оптимального. Однако при больших N_j оно оказывается приемлемым. Кроме того, нет смысла искать точное целочисленное решения, когда исходные данные заданы со значительными погрешностями. Для выполнения ограничения (27) рациональные значения числа защищаемых элементов можно выбирать по формуле

N_gj^* » ENT(g_j^* N_j),

где ENT(x) – целая часть числа x, g_j^* - оптимальное решение задачи (31), полученное методом линейного программирования.

Пример. Пусть для рассматриваемой территории характерны m=5 опасных природных явлений: 1 – геофизические (землетрясения), 2 - геологические (оползни), 3 - метеорологические (ураганы), 4 – гидрологические (наводнения), 5 – природные пожары. Средний ущерб от разрушения одного объекта инфраструктуры составляет с₀ = 1×10⁵ руб. В очередном году на защиту от ЧС выделяется C_выд = 1×10⁶ руб.

Для приведенных исходных данных определим рациональную защищенность территории по отношению к различным источникам природных ЧС и рациональное распределение выделяемых средств на защиту.

Решение. По полученным соотношениям рассчитаем компоненты векторов c и c_g (приведены в табл. 15).

Тогда с = (-0,05×10⁶, 0,8×10⁶, 1,9×10⁶, 3×10⁶, 2,9×10⁶),

, b = (1×10⁶, 1, 1, 1, 1, 1)^т.

По программе ЭВМ определим вектор g, компоненты которого приведены в табл. 15. Таким образом, при выделенных ресурсах в очередном году целесообразно защитить от геологических, метеорологических явлений и природных пожаров все объекты, от наводнений 70 % объектов. Защита от землетрясений не рациональна. Рациональная доля выделяемых ресурсов на защиту от j-й опасности вычисляется по формуле С_выдj = g_j N_j d_gj (приведена в табл. 15). Для принятых исходных данных n = 12,5, а эффективность затрат на защиту (аналог целевой функции) C_ПУ/С_g = 87.

Таблица 15