Графики обратных тригонометрических функций

Построим график арксинуса

Перечислим основные свойства функции :

Область определения: , не существует значений вроде или

Область значений: , то есть, функция ограничена.

Арксинус – функция нечетная, здесь минус опять же выносится: .

В практических вычислениях полезно помнить следующие значения арксинуса: , , . Другие распространенные значения арксинуса (а также других «арков») можно найти с помощью таблицы значений обратных тригонометрических функций.

Построим график арккосинуса

Очень похоже на арксинус, свойства функции сформулируйте самостоятельно. Остановлюсь на единственном моменте. В данной статье очень много разговоров шло о четности и нечетности функций, и, возможно, у некоторых сложилось впечатление, что функция обязательно должна быть четной или нечетной.

В общем случае, это, конечно, не так. Чаще всего, функция, которая вам встретится на практике – «никакая». В частности, арккосинус не является четной или нечетной функцией, он как раз «никакой», или, строго говоря – это «функция общего вида по отношению к свойству чётности».

Построим график арктангенса

Всего лишь перевернутая ветка тангенса.

Перечислим основные свойства функции :

Область определения: , или «множество всех действительных чисел»

Область значений: , то есть, функция ограничена.

У рассматриваемой функции есть две асимптоты: , .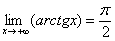

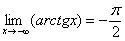Арктангенс – функция нечетная: .

Самые «популярные» значения арктангенса, которые встречаются на практике, следующие: , .

К графику арккотангенса приходиться обращаться значительно реже, но, тем не менее, вот его чертеж:

Свойства арккотангенса вы вполне сможете сформулировать самостоятельно. Отметим, что арккотангенс, как и арккосинус, не является четной или нечетной функцией, а является «функцией общего вида по отношению к свойству чётности».

Пределы функций

Теория пределов – это один из разделов математического анализа. Попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике. Мы не будем рассматривать строгое определение предела, а сделаем две вещи:

* Поймём, что такое предел.

* Научимся решать основные типы пределов.

 

Итак, что же такое предел?

Пример: .

 

Любой предел состоит из трех частей:

1) Всем известный значок предела (это сокращение латинского слова limes - предел).

2) Запись под значком предела, в данном случае . Запись читается: «икс стремится к единице». Чаще всего – именно x, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность ( ).

3) Функции под знаком предела, в данном случае .

Сама запись читается так: «предел функции при икс стремящемся к единице».

Разберем следующий важный вопрос – а что значит выражение «икс стремитсяк единице»? И что вообще такое «стремится»?

Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала , затем , , …, , ….

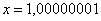То есть выражение «икс стремитсяк единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.