Постоянное число можно (и нужно) вынести за знак производной

, где 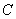– постоянное число (константа)

Пример 2

Найти производную функции

Смотрим в таблицу производных. Производная косинуса там есть, но у нас .

Решаем:

Самое время использовать правило, выносим постоянный множитель за знак производной:

А теперь превращаем наш косинус по таблице:

Ну и результат желательно немного «причесать» – ставим минус на первое место, заодно избавляясь от скобок:

Готово.

Производная суммы равна сумме производных

Пример 3

Найти производную функции

Решаем. Как Вы, наверное, уже заметили, первое действие, которое всегда выполняется при нахождении производной, состоит в том, что мы заключаем в скобки всё выражение и ставим штрих справа вверху:

Применяем второе правило:

Обратите внимание, что для дифференцирования все корни, степени нужно представить в виде , а если они находятся в знаменателе, то переместить их вверх. Как это сделать – рассмотрено в моих методических материалах.

Теперь вспоминаем о первом правиле дифференцирования – постоянные множители (числа) выносим за знак производной:

Обычно в ходе решения эти два правила применяют одновременно (чтобы не переписывать лишний раз длинное выражение).

Все функции, находящиеся под штрихами, являются элементарными табличными функциями, с помощью таблицы осуществляем превращение:

Можно всё оставить в таком виде, так как штрихов больше нет, и производная найдена. Тем не менее, подобные выражения обычно упрощают:

Все степени вида желательно снова представить в виде корней, степени с отрицательными показателями – сбросить в знаменатель. Хотя этого можно и не делать, ошибкой не будет.

Пример 4

Найти производную функции

Попробуйте решить данный пример самостоятельно (ответ в конце урока)

Производная произведения функций

Вроде бы по аналогии напрашивается формула …., но неожиданность состоит в том, что:

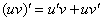
Я не буду объяснять, почему именно так, наша задача научиться решать производные, а не разбираться в теории.

Пример 5

Найти производную функции

Здесь у нас произведение двух функций, зависящих от .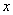
Сначала применяем наше странное правило, а затем превращаем функции по таблице производных:

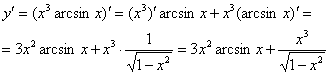
Сложно? Вовсе нет, вполне доступно даже для чайника.

Пример 6

Найти производную функции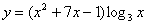

В данной функции содержится сумма и произведение двух функций – квадратного трехчлена и логарифма . Со школы мы помним, что умножение и деление имеют приоритет перед сложением и вычитанием.

Здесь всё так же. СНАЧАЛА мы используем правило дифференцирования произведения:

Теперь для скобки используем два первых правила:

В результате применения правил дифференцирования под штрихами у нас остались только элементарные функции, по таблице производных превращаем их в другие функции:

Готово.

При определенном опыте нахождения производных, простые производные вроде не обязательно расписывать так подробно. Вообще, они обычно решаются устно, и сразу записывается, что .

Пример 7

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока)