Производная степенно-показательной функции

Данную функцию мы еще не рассматривали. Степенно-показательная функция – это функция, у которой и степень и основание зависят от «икс». Классический пример, который вам приведут в любом учебнике или на любой лекции:

Как найти производную от степенно-показательной функции?

Необходимо использовать только что рассмотренный приём – логарифмическую производную. Навешиваем логарифмы на обе части:

Как правило, в правой части из-под логарифма выносится степень:

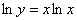
В результате в правой части у нас получилось произведение двух функций, которое будет дифференцироваться по стандартной формуле .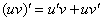

Находим производную, для этого заключаем обе части под штрихи:

Дальнейшие действия несложны:

Окончательно:

Если какое-то преобразование не совсем понятно, пожалуйста, внимательно перечитайте объяснения Примера №11.

В практических заданиях степенно-показательная функция всегда будет сложнее, чем рассмотренный лекционный пример.

Пример 13

Найти производную функции

Используем логарифмическую производную.

В правой части у нас константа и произведение двух множителей – «икса» и «логарифма логарифма икс» (под логарифм вложен еще один логарифм). При дифференцировании константу, как мы помним, лучше сразу вынести за знак производной, чтобы она не мешалась под ногами; и, конечно, применяем знакомое правило :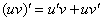

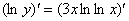
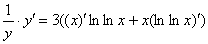
Как видите, алгоритм применения логарифмической производной не содержит в себе каких-то особых хитростей или уловок, и нахождение производной степенно-показательной функции обычно не связано с «мучениями».

Заключительные два примера предназначены для самостоятельного решения.

Пример 14

Найти производную функции

Пример 15

Найти производную функции

Образцы решения и оформления совсем близко.

Не такое и сложное это дифференциальное исчисление

Решения и ответы:

Пример 1:
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, ,

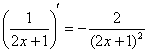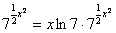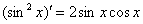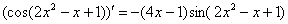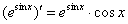Пример 3:

Пример 5:

Примечание: перед дифференцированием можно было раскрыть скобки и использовать правило 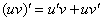один раз.

Пример 7:

Пример 9: Сначала преобразуем функцию. Используем свойства логарифмов:

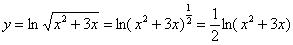
Найдем производную. Используем правило дифференцирования сложной функции:

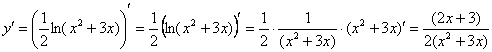
Пример 10: Сначала преобразуем функцию:

Найдем производную:

Пример 12: Используем логарифмическую производную. Преобразуем функцию:




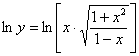
Находим производную:

Пример 14: Используем логарифмическую производную:

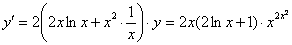
Пример 15: Используем логарифмическую производную: