Понижение степени подынтегральной функции

Данный приём работает, когда подынтегральные функции нафаршированы синусами и косинусами в чётных степенях. Для понижения степени используют тригонометрические формулы 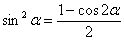, 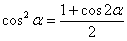и

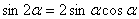, причем последняя формула чаще используется в обратном направлении, как: .

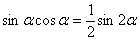Пример 7

Найти неопределенный интеграл.

Решение:

В принципе, ничего нового здесь нет, за исключением того, что мы применили формулу 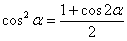, понизив степень подынтегральной функции. Обратите внимание, что мы сократили решение. По мере накопления опыта интеграл от cos2x можно находить устно, это экономит время и вполне допустимо при чистовом оформлении заданий. В данном случае целесообразно не расписывать и правило 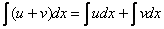, сначала устно берем интеграл от 1, затем – от cos2x.

Пример 8

Найти неопределенный интеграл

.

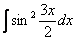Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Далее – пример с повышением степени:

Пример 9

Найти неопределенный интеграл

.

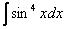Сначала решение, потом комментарии:

(1) Готовим подынтегральную функцию для применения формулы .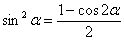

(2) Собственно применяем формулу.

(3) Возводим знаменатель в квадрат и выносим константу за знак интеграла. Можно было поступить несколько иначе, но так удобнее.

(4) Используем формулу .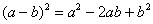

(5) В третьем слагаемом снова понижаем степень, но уже с помощью формулы .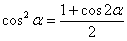

(6) Приводим подобные слагаемые (здесь мы почленно разделили 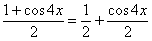и выполнили сложение ).

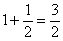(7) Собственно берём интеграл, правило линейности и метод подведения функции под знак дифференциала выполняем устно.

(8) Причесываем ответ.

В неопределенном интеграле нередко ответ можно записать несколькими способами.

В только что рассмотренном примере окончательный ответ

можно было записать иначе – раскрыть скобки и даже сделать это до интегрирования выражения. То есть вполне допустима следующая концовка примера:

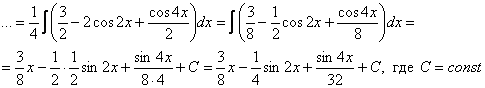
Пример 10

Найти неопределенный интеграл

.

Это пример решается двумя способами, и у Вас могут получиться два разных ответа(точнее, они будут выглядеть совершенно по-разному, но с математической точки зрения являться эквивалентными). Скорее всего, Вы не увидите наиболее рациональный способ и помучаетесь с раскрытием скобок, использованием других тригонометрических формул. Наиболее эффективное решение приведено в конце урока.

Подытоживая параграф, сделаем вывод: любой интеграл вида 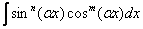, где n и m – чётные числа, решается методом понижения степени подынтегральной функции.

На практике мне встречались интегралы с 8 и 10 степенями, решать их приходилось ужасно долго, понижая степень несколько раз, в результате получались длинные-длинные ответы.