 |
Главная |
Интегрирование сложных тригонометрических функций
|
из
5.00
|
На уроке Интегралы от тригонометрических функциймы разобрали интеграл от тангенса в квадрате. В том примере для нахождения интеграла мы применяли тригонометрическую формулу
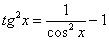 .
.
Интеграл от тангенса в четвертой, пятой степени (редко в более высоких степенях) решается с помощью этой же формулы!
Пример 15
Найти неопределенный интеграл
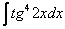 .
.
Идея решения подобных интегралов состоит в том, чтобы с помощью формулы 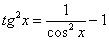 «развалить» исходный интеграл на несколько более простых интегралов:
«развалить» исходный интеграл на несколько более простых интегралов:
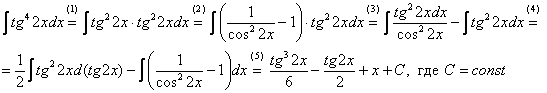
(1) Готовим подынтегральную функцию к применению формулы.
(2) Для одного из множителей используем формулу
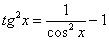
(3) Раскрываем скобки и сразу же используем свойство линейности неопределенного интеграла.
(4) В первом интеграле используем метод подведения функции под знак дифференциала, во втором интеграле еще раз используем формулу
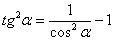 , в данном случае
, в данном случае 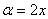 .
.
(5) Берём все три интеграла и получаем ответ.
Пример 16
Найти неопределенный интеграл
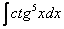
Это пример для самостоятельного решения.
Для котангенса существует аналогичная формула:
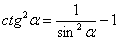 . Полное решение и ответ в конце урока.
. Полное решение и ответ в конце урока.
Если возникли затруднения или недопонимание, следует вернуться к уроку Интегралы от тригонометрических функций. На вышеупомянутом уроке мы рассматривали универсальную тригонометрическую подстановку для решения определенного вида интегралов от тригонометрических функций. Недостаток универсальной тригонометрической подстановки заключается в том, что при её применении часто возникают громоздкие интегралы с трудными вычислениями. И в ряде случаев универсальной тригонометрической подстановки можно избежать! Рассмотрим еще один канонический пример - интеграл от единицы, деленной на синус:
Пример 17
Найти неопределенный интеграл
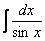 .
.
Здесь можно использовать универсальную тригонометрическую подстановку и получить ответ, но существует более рациональный путь. Приведём это решение с комментариями к каждому шагу:

(1) Используем тригонометрическую формулу синуса двойного угла
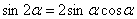 .
.
(2) Проводим искусственное преобразование: В знаменателе делим и умножаем на
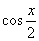 .
.
(3) По известной формуле в знаменателе превращаем дробь в тангенс.
(4) Подводим функцию под знак дифференциала.
(5) Берём интеграл.
Пример 18
Найти неопределенный интеграл
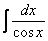 .
.
Указание: Самым первым действием следует использовать формулу приведения
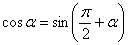
и аккуратно провести аналогичные предыдущему примеру действия.
Пример 19
Найти неопределенный интеграл
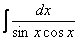 .
.
Ну, это совсем простой пример. Полные решения и ответы в конце урока.
Думаем, теперь ни у кого не возникнет проблем с интегралами:
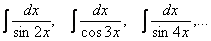 и т.п.
и т.п.
В чём состоит идея метода? Идея состоит в том, чтобы с помощью тождественных преобразований и тригонометрических формул организовать в подынтегральной функции только тангенсы и производную тангенса
 .
.
То есть, речь идет о замене:
 .
.
В Примерах 17-19 мы фактически и применяли данную замену, но интегралы были настолько просты, что дело обошлось эквивалентным действием – подведением функции под знак дифференциала.
Примечание: аналогичные рассуждения можно провести и для котангенса.
Существует и формальное правило для применения вышеуказанной замены:
|
из
5.00
|
Обсуждение в статье: Интегрирование сложных тригонометрических функций |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

