 |
Главная |
Интегрирование биномиальных интегралов
|
из
5.00
|
Так называемый биномиальный интеграл имеет следующий вид:
 .
.
Такой интеграл берётся в трёх случаях.
1) Случай первый. Самый лёгкий. Если степень – целое число.Например:
– целое число.Например:
 .
.
Представим интеграл в стандартном виде (это лучше делать на черновике):
 .
.
Мы видим, что степень  – целая, а, значит, действительно имеет место первый случай. На самом деле биномиальный интеграл первого типа решается практически так же, как интегралы в примерах 5, 6, поэтому приводить почти такие же решения нет смысла. Просто покажем, какую замену здесь нужно провести. Смотрим на знаменатели дробей в показателях степеней:
– целая, а, значит, действительно имеет место первый случай. На самом деле биномиальный интеграл первого типа решается практически так же, как интегралы в примерах 5, 6, поэтому приводить почти такие же решения нет смысла. Просто покажем, какую замену здесь нужно провести. Смотрим на знаменатели дробей в показателях степеней:
 .
.
Записываем знаменатели: 2, 5. Находим наименьшее общее кратное этих чисел. Очевидно, это 10: оно делится и на 2 и на 5, кроме того – десятка самая маленькая в этом смысле.
После замены 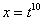 все корни гарантировано пропадут. Повторюсь, примеров для первого случая не будет, так как они очень похожи на недавно разобранные интегралы.
все корни гарантировано пропадут. Повторюсь, примеров для первого случая не будет, так как они очень похожи на недавно разобранные интегралы.
Случай второй для биномиальных иноегралов
 .
.
Если – целое число, то необходимо провести замену
– целое число, то необходимо провести замену 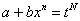 ,
,
где – знаменатель дроби
– знаменатель дроби  .
.
Сейчас во всём разберемся.
Пример 7
Найти неопределенный интеграл
 .
.
Представим интеграл в стандартном виде  :
:
 .
.
Вообще говоря, формально правильнее было записать 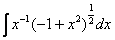 , но перестановка слагаемых в скобках не играет никакой роли.
, но перестановка слагаемых в скобках не играет никакой роли.
Выписываем степени:
 ,
,  ,
,  .
.
Сразу проверяем, не относится ли наш интеграл к первому случаю?
 – целое? Нет.
– целое? Нет.
Проверяем второй случай:
 – целое.
– целое.
Значит, у нас второй случай.
Согласно правилу для второго случая, необходимо провести замену 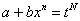 , где
, где  – знаменатель дроби p. В рассматриваемом примере p = 1/2, и знаменатель этой дроби равен «двойке». Таким образом, чтобы гарантировано избавиться от корня, нужно провести замену
– знаменатель дроби p. В рассматриваемом примере p = 1/2, и знаменатель этой дроби равен «двойке». Таким образом, чтобы гарантировано избавиться от корня, нужно провести замену  .
.
Оформляем решение:
 .
.
Проведем замену  .
.
После этой подстановки с корнем у нас будет всё в порядке:  .
.
Теперь нужно выяснить, во что превратится оставшаяся частьподынтегрального выражения  ?
?
Берем нашу замену  и навешиваемдифференциалы на обечасти:
и навешиваемдифференциалы на обечасти:
 .
.
Но вот незадача, у нас  , а нам нужно выразить
, а нам нужно выразить  .
.
Умножаем обе части на  :
:

Таким образом:  . Уже лучше, но хотелось бы выразить
. Уже лучше, но хотелось бы выразить  только через
только через , а в правой части
, а в правой части  – «икс» в квадрате внизу. Что делать? Вспоминаем нашу замену
– «икс» в квадрате внизу. Что делать? Вспоминаем нашу замену  и выражаем из неё
и выражаем из неё  .
.
Окончательно:
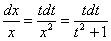 .
.
Головоломно, но, увы, другие алгоритмы еще запутаннее.
Собственно, всё готово, продолжаем решение:

(1) Проводим подстановку согласно замене.
(2) Записываем компактно числитель.
(3) Раскладываем знаменатель в сумму.
(4) Почленно делим числитель на знаменатель.
(5) Интегрируем по таблице.
(6) Проводим обратную замену: если  , то
, то  .
.
Пример 8
Найти неопределенный интеграл
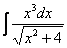 .
.
Это пример для самостоятельного решения.
Полное решение и ответ в конце урока.
3) Случай третий.Самый сложный
 .
.
Если – целое число, то необходимо провести замену
– целое число, то необходимо провести замену  ,
,
где – знаменатель дроби
– знаменатель дроби  .
.
Пример 9
Найти неопределенный интеграл
 .
.
Представим интеграл в стандартном виде  :
:
 .
.
Выписываем степени и коэффициенты:
 ,
,  ,
,  ,
,  ,
,  .
.
1) Не относится ли наш интеграл к первому случаю?
 – целое? Нет.
– целое? Нет.
2) Проверяем второй случай:
 ; – целое? Нет.
; – целое? Нет.
3) 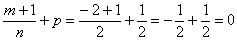 – целое! Значит, у нас третий случай.
– целое! Значит, у нас третий случай.
Согласно правилу для третьего случая, необходимо провести замену  , где
, где  – знаменатель дроби p. В рассматриваемом примере p = 1/2, и знаменатель этой дроби равен опять же «двойке». Коэффициенты (будьте внимательны)
– знаменатель дроби p. В рассматриваемом примере p = 1/2, и знаменатель этой дроби равен опять же «двойке». Коэффициенты (будьте внимательны)  ,
,  .
.
Таким образом, чтобы гарантировано избавиться от корня, нужно провести замену  .
.
Оформляем решение:

Проведем замену:  .
.
Разбираемся с корнем. Это труднее, чем в предыдущих случаях.
Сначала из нашей замены  нужно выразить «икс квадрат»:
нужно выразить «икс квадрат»:
 .
.
Теперь подставляем  под корень:
под корень:
 .
.
На втором этапе выясняем, во что превратится оставшаяся частьподынтегрального выражения 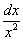 . Берем нашу замену
. Берем нашу замену  и навешиваем дифференциалы на обе части:
и навешиваем дифференциалы на обе части:

Опять проблема, в правой части у нас есть «икс», а нам нужно всё выразить через «тэ».
Берем ранее найденное выражение
 и выражаем
и выражаем  .
.
Окончательно:
 .
.
В итоге мы выразили через «тэ» и  и
и  , всё готово для продолжения решения:
, всё готово для продолжения решения:

(1) Проводим подстановку согласно замене.
(2) Упрощаем выражение.
(3) Меняем знак в знаменателе и выносим минус за пределы интеграла (можно было не делать, но так удобнее).
(4) Проводим обратную замену. В третьем случае биномиального интеграла это тоже труднее. Если изначальная замена  , то
, то  .
.
(5) Избавляемся от четырехэтажности в логарифме.
Пример 10
Найти неопределенный интеграл
 .
.
Это пример для самостоятельного решения. Подсказка: здесь  .
.
Полное решение и ответ только для выживших студентов.
Что делать, если биномиальный интеграл

не подходит ни под один из рассмотренных трех случаев? Это грустный четвертый случай. Такой интеграл является неберущимся.
Есть другие разновидности интегралов с корнями, например, когда корень является аргументом какой-либо функции. Или под корнем находится дробь. Найти такие примеры можно на странице Сложные интегралы.
Решения и ответы:
Пример 2: Решение:

Проведем замену: 

Пример 4: Решение:

Проведем замену:  . Навешиваем дифференциалы на обе части:
. Навешиваем дифференциалы на обе части:
 .
.
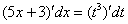 .
.
 .
.
Вот почему дифференциалы нужно именно НАВЕШИВАТЬна обе части и добросовестно раскрывать эти дифференциалы. Немало чайников здесь формально напишет 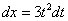 и допустит ошибку.
и допустит ошибку.

Пример 6: Решение:

Замена: 

Примечание: на самом деле данное решение не совсем рационально. Перед тем, как раскладывать числитель в сумму, лучше было поменять у знаменателя знак и сразу вынести минус за пределы интеграла:
 – в таком виде подбирать числитель значительно проще.
– в таком виде подбирать числитель значительно проще.
Пример 8: Решение:

 ,
,  ,
,  ,
, 
1)  – целое? Нет. 2)
– целое? Нет. 2)  – целое, значит у нас второй случай. Замена:
– целое, значит у нас второй случай. Замена:  ,
,  ,
, 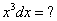



Если  , то
, то  .
.
Окончательно:  .
.

Пример 10: Решение:


 ,
,  ,
,  ,
, 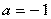 ,
,  .
.
1)  – целое? Нет.
– целое? Нет.
2) 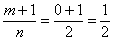 – целое? Нет.
– целое? Нет.
3)  – целое!
– целое!
Замена:  , в данном случае:
, в данном случае:
 .
.
Разбираемся с корнем. Из  :
:
 .
.
Тогда:
 .
.
Оставшаяся часть подынтегрального выражения: 
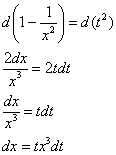 .
.
Чему равно  ?
?
 .
.
Окончательно:

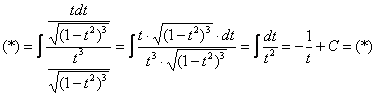
Обратная замена. Если  , то
, то  .
.

Сложные интегралы
Данная статья завершает тему неопределенных интегралов. Предполагается, что читатель сего текста хорошо подготовлен и умеет применять основные приемы интегрирования. Людям, которые не очень уверенно разбираются в интегралах, следует обратиться к самому первому уроку – Неопределенный интеграл. Примеры решений, где можно освоить тему практически с нуля. Более опытные студенты могут ознакомиться с приемами и методами интегрирования, которые в этом курсе еще не встречались.
|
из
5.00
|
Обсуждение в статье: Интегрирование биномиальных интегралов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

