Практическое занятие 2

Абсолютные и относительные показатели

Вариации

Цель работы: формирование навыков по вычислению абсолютных и относительных показателей вариации.

Краткое изложение теоретических вопросов:

Вариация - это различие значений величин X у отдельных единиц статистической совокупности. Для изучения силы вариации рассчитывают следующие показатели вариации: размах вариации, среднее линейное отклонение, линейный коэффициент вариации, дисперсия, среднее квадратическое отклонение, квадратический коэффициент вариации.

Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:

Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.

Cреднее линейное отклонение - это средний модуль отклонений значений X от среднего арифметического значения. Его можно рассчитывать по формуле средней арифметической простой - получим среднее линейное отклонение простое:

Если исходные данные X сгруппированы (имеются частоты f), то расчет среднего линейного отклонения выполняется по формуле средней арифметической взвешенной - получим среднее линейное отклонение взвешенное:

Линейный коэффициент вариации - это отношение среднего линейного отклонение к средней арифметической:

С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.

Дисперсия - это средний квадрат отклонений значений X от среднего арифметического значения. Дисперсию можно рассчитывать по формуле средней арифметической простой - получим дисперсию простую:

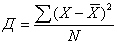
Если исходные данные X сгруппированы (имеются частоты f), то расчет дисперсии выполняется по формуле средней арифметической взвешенной - получим дисперсию взвешенную:

Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:

Если значения X - это доли совокупности, то для расчета дисперсии используют частную формулу дисперсии доли:

Выше уже было рассказано о формуле средней квадратической, которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:

Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:

Коэффициент вариации - это самый популярный относительный показатель вариации:

Критериальным значением квадратического коэффициента вариации V служит 0,333 или 33,3%, то есть если V меньше или равен 0,333 - вариация считает слабой, а если больше 0,333 - сильной. В случае сильной вариации изучаемая статистическая совокупность считается неоднородной, а средняя величина - нетипичной и ее нельзя использовать как обобщающий показатель этой совокупности.

Задание 1

На основе сгруппированных данных полученных при выполнении практической работы №1 рассчитать абсолютные и относительные показатели вариации. Сделать вывод об однородности совокупности и о типичности и достоверности полученных ранее групповых и общих средних значениях факторного и результативного признаков.