 |
Главная |
Определение оптимального размера заказываемой партии
|
из
5.00
|
Страховые запасы служат своего рода «аварийным» источником снабжения в тех случаях, когда спрос на данный товар превышает ожидания. На практике спрос на товары удается точно спрогнозировать чрезвычайно редко. Это же относится и к точности предсказания сроков реализации заказов. Отсюда возникает необходимость создания страховых товарно-материальных запасов.
Можно выделить несколько причин, по которым предприниматели заказывают больший объем товаров, чем требуется на данный момент:
• задержка получения заказанных товаров;
• возможность получить товар в неполном объеме, что вынуждает заказчиков (в особенности посредников) хранить какое-то время те или иные товары на складе;
• предоставление скидок, получаемых заказчиком при покупке им крупной партии товаров;
• одинаковая величина транспортных, накладных и других расходов независимо от объема партии. (Например, стоимость одного контейнера будет одна и та же независимо оттого, загружен полностью контейнер или нет.)
Создание запасов требует дополнительных финансовых затрат, поэтому возникает необходимость в сокращении этих затрат с помощью достижения оптимального баланса между объемом запаса, с одной стороны, и финансовыми затратами -с другой. Этот баланс достигается выбором оптимального объема партий заказанных товаров или определением экономического (оптимального) размера заказа — EOQ (Economic Order Quantity), который вычисляется по формуле

где А — затраты на производство; D — средний уровень спроса;  — удельные затраты на производство; r — затраты на хранение.
— удельные затраты на производство; r — затраты на хранение.
Определение точного уровня необходимых резервных запасов зависит от трех факторов:
1) возможного колебания сроков восстановления уровня запасов;
2) колебания спроса на соответствующие товары на протяжении срока реализации заказа;
3) осуществляемой данной компанией стратегии обслуживания заказчиков.
Определить точный уровень необходимых резервных запасов в условиях нестабильности сроков реализации заказов, изменчивого спроса на товары и материалы достаточно сложно. Для нахождения удовлетворительных решений проблем, связанных с резервными товарно-материальными запасами, необходимо использовать моделирование или имитацию различных сценариев.
Оптимальный размер партии поставляемых товаров и соответственно оптимальная частота завоза зависят от следующих факторов: объема спроса (оборота); транспортно-заготовительных расходов; расходов на хранение.
В качестве критерия оптимальности выбирают минимум суммы транспортно-заготовительных расходов и расходов на хранение. Транспортно-заготовительные расходы при увеличении размера заказа уменьшаются, так как закупки и перевозки товаров осуществляются более крупными партиями и, следовательно, реже. Расходы на хранение растут прямо пропорционально размеру заказа. Для решения этой задачи необходимо минимизировать функцию, представляющую сумму транспортно -заготовительных расходов и расходов на хранение, т.е. определить условия, при которых

где Собщ — общие затраты на транспортировку и хранение;
Схран- затраты на хранение запаса; Странсп -транспортно-заготовительные расходы.
Предположим, что за определенный период времени величина оборота составляет Q. Размер одной заказываемой партии — S. Допустим, что новая партия завозится после того, как предыдущая полностью закончилась. Тогда средняя величина запаса составит S/2.
Введем размер тарифа (А/) за хранение товара. Он измеряется долей, которую составляют издержки по хранению за период Т в стоимости среднего запаса за тот же период. Стоимость хранения товаров за период Т можно рассчитать по формуле

Размер транспортно-заготовительных расходов за период Т , определяется по формуле

где К — транспортно-заготовительные расходы, связанные с paзмещением и доставкой одного заказа;  - количество заказов за период времени.
- количество заказов за период времени.
Подставив данные  , получим:
, получим:
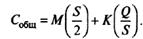
Минимум Собщ имеется в точке, в которой ее первая производная по равна нулю, а вторая производная больше нуля. Первая производная:

Найдем значение Soбщ (оптимальный размер заказа), обращающее производную целевой функции в нуль:

Эта формула, позволяющая рассчитать оптимальный размер заказа, в теории управления запасами известна как формула Уилсона.
|
из
5.00
|
Обсуждение в статье: Определение оптимального размера заказываемой партии |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

