Дифференциальное исчисление функций нескольких переменных

 

Частные производные функции

Частные производные функции по аргументам x, y и

Z соответственно определяются как соответствующие пределы ( если они существуют):

(6.4.1)

(6.4.2)

. (6.4.3)

 

При фиксированных значениях всех аргументов, кроме, например,

Х, функция становится функцией одной переменной. Производная этой функции по переменной х и есть частная производная по аргументу х. Поэтому вычисления частных производных производится по тем же правилам, что и вычисление производной функции одной переменной.

 

Дифференциал функции

Пусть функция дифференцируема в точке т.е полное приращение в этой точке можно представить в следующем виде:

 

Дифференциал этой функции вычисляется по формуле

. (6.4.4)

 

Обозначим через .

Координаты некоторой точки М₁= , тогда следует

 

.

Алгоритм использования дифференциала в приближенных вычислениях

Пусть требуется найти приближенное значение величины А, тогда необходимо выполнить следующие действия:

1. Представить А в виде значения некоторой функции в точке М₁:

2. Подобрать точку М₀ так, чтобы она была достаточно близкой к точке M₁ и значение вычислялось легко, и вычислить

3. Найти

4. Вычислить согласно формуле.

Частные производные и дифференциалы высших порядков

Частными производными второго порядка от функции 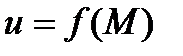называются частные производные от ее частных производных первого порядка.

Рассмотрим функцию двух переменных , которая имеет частные производные во всех точках области определения D. Частные производные второго порядка в этом случае записываются следующим образом:

 

. (6.4.5)

.(6.4.6)

 

Аналогично определяются и записываются частные производные третьего порядка, например:

 

(6.4.7)

и высших порядков:

(6.4.8)

 

Дифференциалом второго порядка от функции 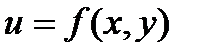называется дифференциал от ее полного дифференциала, т.е

. Аналогично определяются дифференциалы третьего и высших порядков:

 

или . (6.4.9)

 

Производные по направлению. Градиент

Пусть функция определена в некоторой окрестности точки М₀; -некоторый луч М₀М, длина отрезка М₀М,

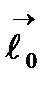-единичный вектор, имеющий направление луча . Предел

, если он существует, называется производной функции 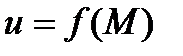по напрвлению точке М₀ и обозначается В декартовой прямоугольной системе координат

,

где .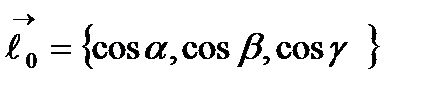

Градиентом функции в точке M₀ называется вектор, характеризующий направление наибольшего роста функции в этой точке и обозначается . (6.4.10)

Производная функции 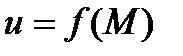в точке М₀ в направлении вектора и градиент связаны соотношением

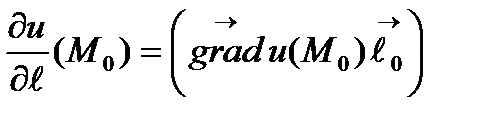. (6.4.11)

 

Пример 6.4.1. Найти дифференциал функции в точке

Решение:

Данная функция является сложной где ,

поэтому .

Найдем .

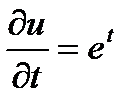Имеем , ;

;

.

 

Пример 6.4.2. Найти приближенное значение величины

Решение:

Положим Выберем

тогда = .

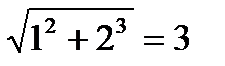Найдем:

 

;

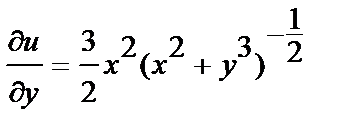По формуле находим

 

.

 

Пример 6.4.3. Найти градиент функции в точке .

Чему равна в этой точке производная функции u в направлении вектора ?

Решение:

= ;

.

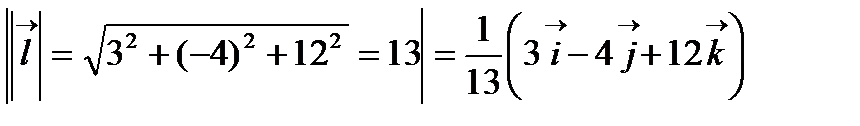Исследование функций

На непрерывность

Пример6.5.1.

Найти точки разрыва функции и исследовать их характер:

а) у = 1/(х + 3); б) у =1/(1 + 2^1/х).

Построить схематично график функций в окрестности точек разрыва.

При решении примеров такого рода следует проверить выполнение условия непрерывности функции в точке

а) Функция у = 1/(х + 3) определена при всех значениях х, кроме х = -3. Так как это функция является элементарной, то она непрерывна в каждой точке своей области определения, состоящей из двух промежутков: (–

Следовательно, единственно возможной точкой разрыва является точка х = – 3. Функция определена в окрестности этой точки, в самой же точке нарушается условие непрерывности – функция в ней не определена. Для исследования характера разрыва найдем левый и правый пределы этой функции при стремлении аргумента к точке х = –3.

Следовательно, при х = –3 функция у = 1/(х + 3) имеет бесконечный разрыв, т.е.

y

 

-3

x

 

 

точка х = –3 есть точка разрыва 2 рода.

 

б) Рассуждая аналогично, получим, что возможной точкой разрыва функции является х = 0. Найдем односторонние пределы этой функции в точке х = 0:

 

y

 

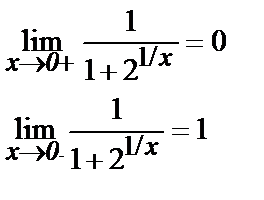
x

 

 

Таким образом, левый и правый пределы исследуемой функции при х = 0 конечны.

Поэтому х = 0 – точка скачка функции, разрыв I рода.