 |
Главная |
Метод интегрирования по частям
|
из
5.00
|
Этот метод основан на следующей формуле:  (*)
(*)
Пусть  и
и 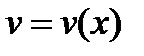 - функции от х, имеющие непрерывные производные
- функции от х, имеющие непрерывные производные  и
и  .
.
Известно, что 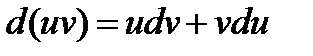 или
или  ; или
; или  .
.
Интегралы  и
и 
 , так как по условию функции u и v дифференцируемы, а значит и непрерывны.
, так как по условию функции u и v дифференцируемы, а значит и непрерывны.
Формула (*) носит название формулы интегрирования по частям.
Метод, основанный на ее применении, называется методом интегрирования по частям.
Он сводит вычисления 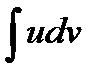 к вычислению другого интеграла:
к вычислению другого интеграла:  .
.
Применение метода интегрирования по частям состоит в том, что под интегральное выражение заданного интеграла стараются представить в виде произведения  , где
, где 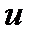 и
и  - некоторые функции от х, причем эти функции выбирают так, чтобы
- некоторые функции от х, причем эти функции выбирают так, чтобы  была для вычисления проще, чем исходный интеграл. При для вычисления
была для вычисления проще, чем исходный интеграл. При для вычисления  предварительно находят
предварительно находят  и
и  .
.
(в качестве “v” берут одну какую-либо из исходных первообразных, находимых по dv,поэтому в дальнейшем при вычислении “v” постоянную С в записи будем опускать).
Замечание. Разбивая под интегральное выражение на множители  , должны понимать, что
, должны понимать, что  должен содержать и
должен содержать и  .
.
Общих правил для разложения под интегрального выражения на множители «u» и «dv», к сожалению, дать нельзя. Этому может научить большая и вдумчивая практика.
При всем этом следует иметь в виду, чтобы  был проще, чем исходный интеграл.
был проще, чем исходный интеграл.
Пример 6.6.22. 
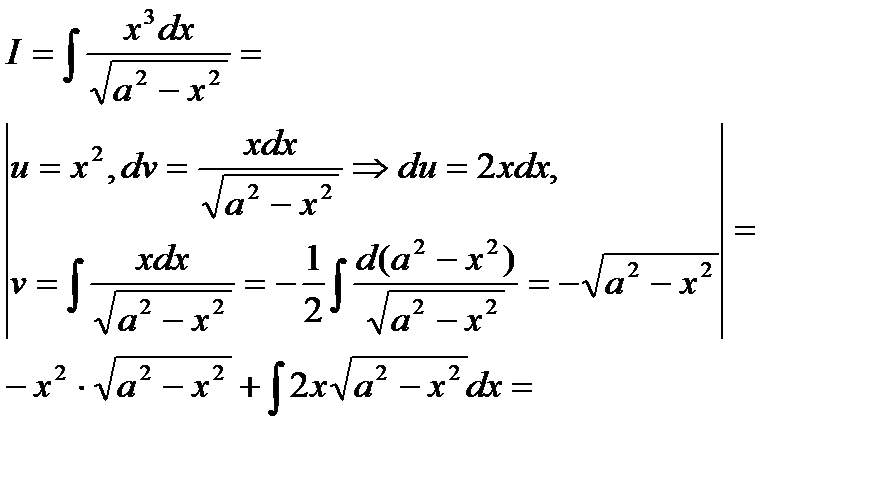


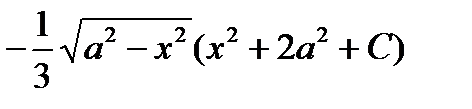
Иногда для получения окончательного результата правило интегрирования по частям применяют последовательно несколько раз.
Метод интегрирования по частям удобно применять, конечно, далеко не всякий раз и умение пользоваться им зависит от наличия опыта.
При вычислении интегралов важно правильно установить, каким методом интегрирования следует пользоваться (так в предыдущем примере тригонометрическая подстановка быстрее приводит к цели).
Рассмотрим наиболее часто встречающиеся интегралы, которые вычисляются интегрированием по частям.
1.Интегралы вида: 
где  - целый (относительно х ) многочлен; а – постоянное число.
- целый (относительно х ) многочлен; а – постоянное число.
Если под знаком интеграла стоит произведение тригонометрической или показательной функции алгебраическую, то за «u» обычно принимают алгебраическую функцию. 
Пример6.6.23. 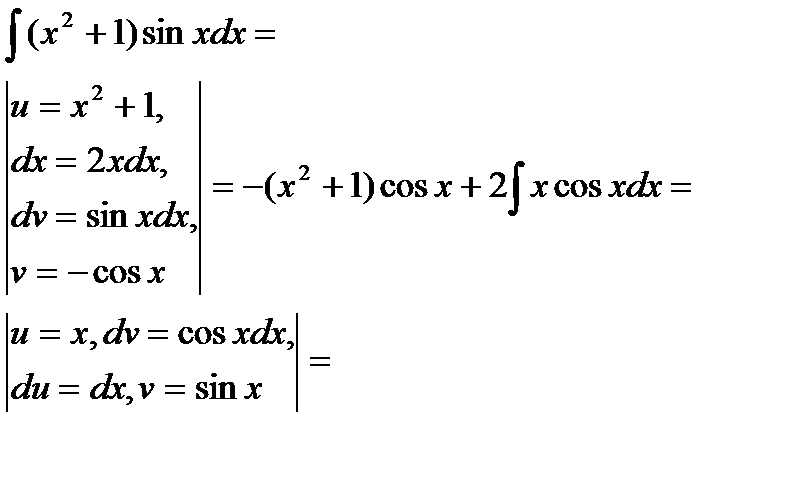

Заметим, что другая разбивка на множители:  не приводит к цели.
не приводит к цели.
Доказано,  .
. 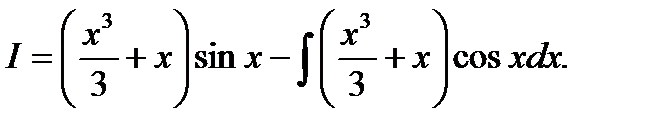
Получим более сложный интеграл.
2.Интегралы вида: 

где  - многочлен.
- многочлен.
Если под знаком интеграла стоит произведение логарифма функции или обратной тригонометрической функции на алгебраическую, то за «u» следует принимать функции  .
.
Пример6.6.23. 
 .
.
3.Интегралы вида: 
Здесь можно использовать любую из 2-х возможных разбивок под интегрального выражения на множители: за «u» можно принять как  , так и
, так и  .
.
Причем вычисление таких интегралов с помощью метода интегрирования по частям приводит к исходному интегралу, то есть получается уравнение относительно искомого интеграла.
Пример 6.6.24.Вычислить  .
.
Пусть  .
.

 .
.
При интегрировании часто приходится последовательно применять метод подстановки и метод интегрирования по частям.
Пример 6.6.25. 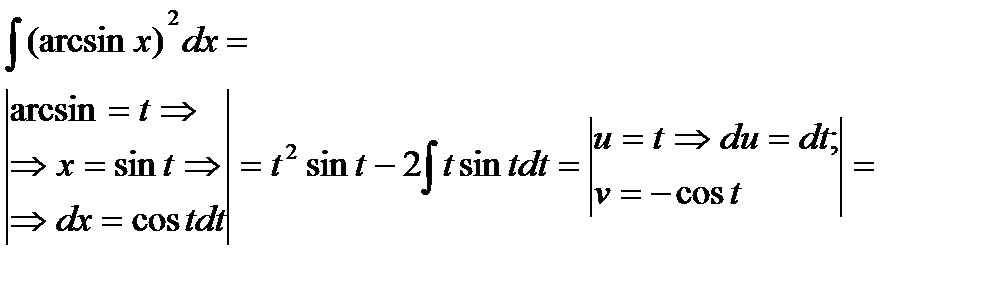


Интегрирование некоторых функций, содержащих квадратный трехчлен
1) 


 .
.
а это - табличные интегралы.
2) 
 коэффициенты действительного числа
коэффициенты действительного числа
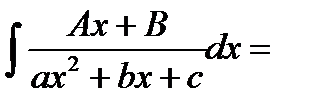 в числителе выделяем производную знаменателя.
в числителе выделяем производную знаменателя.

 .
.

 a,b,c – действительные числа
a,b,c – действительные числа

а)  ; то имеем:
; то имеем: 
б)  . В этом случае имеет смысл рассматривать только тогда, когда дискриминант
. В этом случае имеет смысл рассматривать только тогда, когда дискриминант  трехчлена
трехчлена  положителен:
положителен: 
Теперь имеем: 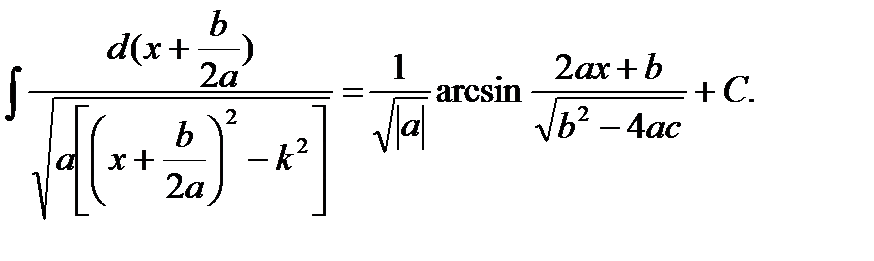

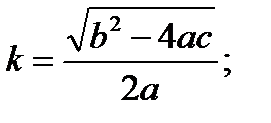
Замечание. На практике не пользуются обычно готовыми результатами, а предпочитают всякий раз проводить аналогичные вычисления вновь.
Пример. 
4) 
Преобразуем числитель так, чтобы из него можно было выделить производную квадратного трехчлена:


В связи с тем, что не существует на практике удобного общего метода вычисления неопределенных интегралов, приходится на ряду с частными методами интегрирования (см.предыдущую лекцию) рассматривать также способы интегрирования некоторых частных классов функций, интегралы от которых часто встречаются на практике.
Важнейшим классом среди них является класс рациональных функций.
«Интегрирование дробно-рациональных функций»
Интегрирование правильной рациональной дроби основано на разложении рациональной дроби в сумму элементарных дробей.
Элементарные (простейшие) дроби и их интегрирование.
Определение. Дроби вида:  ; (1)
; (1)
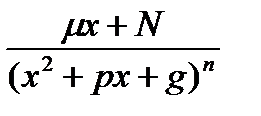 (2), где
(2), где 
(то есть корни трехчлена являются комплексными), называются элементарными.
Рассмотрим интегрирование элементарных дробей
1) 
(при  )
)
2) 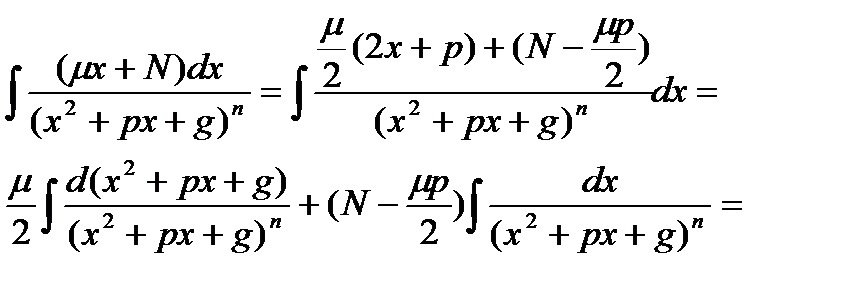
 (где пусть
(где пусть  ).
).
Вычислим интеграл 
 (*)
(*)
Последний интеграл вычисляется с помощью рекуррентной формулы.
Иногда интегрирование по частям позволяет получить соотношение между неопределенным интегралом, содержащим степень некоторой функции, и аналогичным интегралом, но с меньшим показателем степени той же функции. Подобные соотношения называют рекуррентными формулами.
Обозначим через  .
.
Имеем: 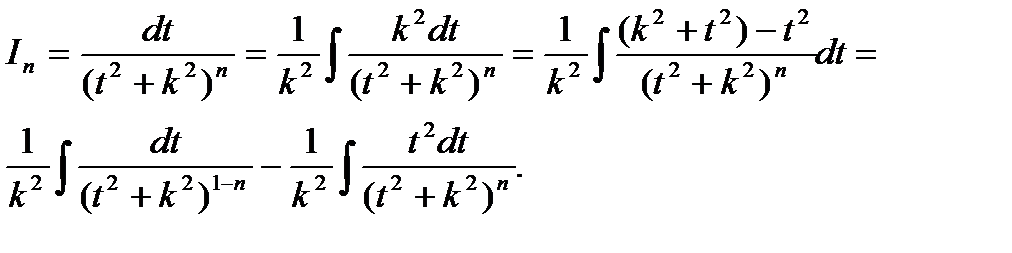
В последнем интеграле положим: 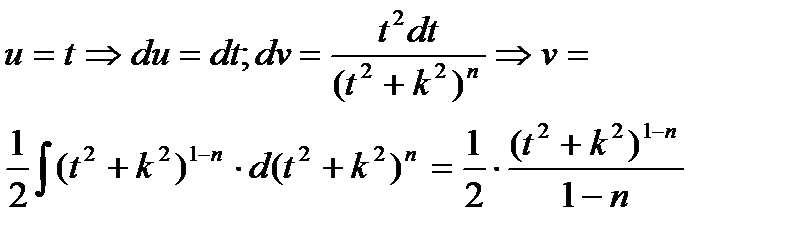
Поэтому 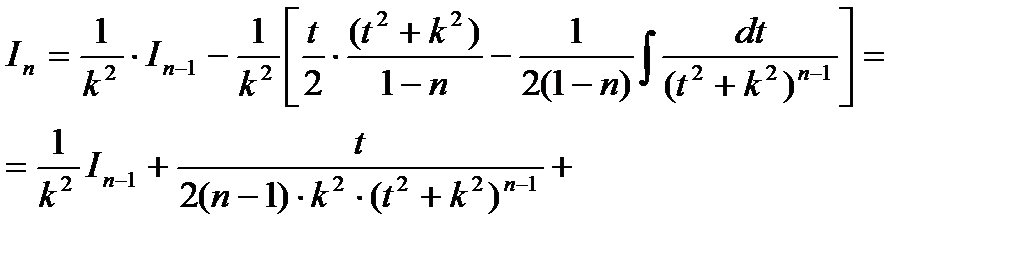
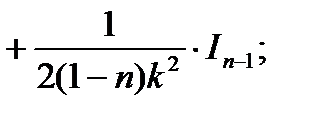 откуда
откуда

Таким образом, мы пришли к рекуррентной формуле: 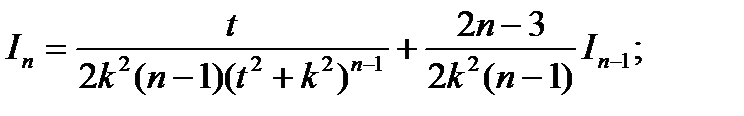 повторное применение которой в конечном счете приводит к «табличному» интегралу:
повторное применение которой в конечном счете приводит к «табличному» интегралу: 
Затем вместо «t» и «k» подставляем их значения.
Пример6.6.26. 

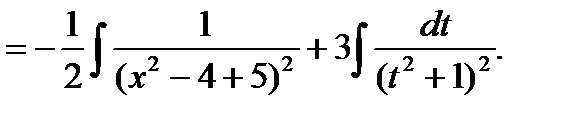
 (по рекурр. формуле).=
(по рекурр. формуле).= 
 .
.
Рациональной дробью называется функция  представимая в виде
представимая в виде  ; где
; где 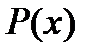 и
и  - многочлены с действительными коэффициентами.
- многочлены с действительными коэффициентами.
Рациональная дробь  называется правильной если степень числителя меньше степени знаменателя.
называется правильной если степень числителя меньше степени знаменателя.
Всякая правильная рациональная дробь может быть представлена в виде суммы конечного числа элементарных дробей.
Разложение правильной дроби на элементарные определяется следующей теоремой, которую рассмотрим без доказательства.
Теорема. Если дробь  - правильная и
- правильная и  , (где трехчлен не имеет действительных корней), то справедливо тождество:
, (где трехчлен не имеет действительных корней), то справедливо тождество:
(I) 
 ;где
;где 
Отметим, что каждому действительному корню, например а, кратности « 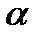 » многочлена
» многочлена  в этом разложении соответствует сумма
в этом разложении соответствует сумма  элементарных дробей вида (1), а каждой паре комплексно сопряженных корней
элементарных дробей вида (1), а каждой паре комплексно сопряженных корней  и
и  (таких, что
(таких, что  ) кратности «
) кратности «  » - сумма элементарных дробей вида (2).
» - сумма элементарных дробей вида (2).
Чтобы осуществлять разложение (I), нужно научиться определять коэффициенты 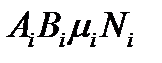 .
.
Существуют различные способы их нахождения. Мы рассмотрим метод неопределенных коэффициентов и метод частных значений.
|
из
5.00
|
Обсуждение в статье: Метод интегрирования по частям |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

