 |
Главная |
Одноканальная СМО с отказами
|
из
5.00
|
Простейшей одноканальной моделью с вероятностными входным потоком и процедурой обслуживания является модель, характеризуемая показательным распределением как длительностей интервалов между поступлениями требований, так и длительностей обслуживания. При этом плотность распределения длительностей интервалов между поступлениями требований имеет вид

где λ — интенсивность поступления заявок в систему (среднее число заявок, поступающих в систему за единицу времени).
Плотность распределения длительностей обслуживания:
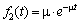 ,
,
где  – интенсивность обслуживания, tоб – среднее время обслуживания одного клиента.
– интенсивность обслуживания, tоб – среднее время обслуживания одного клиента.
Пусть система работает с отказами. Можно определить абсолютную и относительную пропускную способность системы.
Относительная пропускная способность равна доли обслуженных заявок относительно всех поступающих и вычисляется по формуле:  . Эта величина равна вероятности Р0 того, что канал обслуживания свободен.
. Эта величина равна вероятности Р0 того, что канал обслуживания свободен.
Абсолютная пропускная способность (А) — среднее число заявок, которое может обслужить система массового обслуживания в единицу времени:  .
.
Вероятность отказа в обслуживании заявки будет равна вероятности состояния «канал обслуживания занят»:
 .
.
Данная величина Ротк может быть интерпретирована как средняя доля необслуженных заявок среди поданных.
http://math.immf.ru/lections/206.html
Регрессио́нный анализ — статистический метод исследования влияния одной или нескольких независимых переменных X_1, X_2, ..., X_p на зависимую переменную Y. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.
Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными)
Предсказание значения зависимой переменной с помощью независимой(-ых)
Определение вклада отдельных независимых переменных в вариацию зависимой
Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.
Оставаясь в рамках классического регрессионного анализа, уточним рассматриваемую статистическую задачу. Пусть исходными данными являются пары значений  , которые являются результатами измерений. В общем случае число узлов может отличаться от числа откликов, так как измерения могут проводиться несколько раз в одном и том же узле, т. е.
, которые являются результатами измерений. В общем случае число узлов может отличаться от числа откликов, так как измерения могут проводиться несколько раз в одном и том же узле, т. е.  . Значения аргумента
. Значения аргумента  известны точно, а значения отклика
известны точно, а значения отклика  содержат только случайные ошибки:
содержат только случайные ошибки:
 ,
,
т. е.  , где
, где  – истинное значение в узле
– истинное значение в узле  . Обычно ошибки в измерении или задании аргумента либо отсутствуют, либо гораздо меньше по сравнению с ошибками
. Обычно ошибки в измерении или задании аргумента либо отсутствуют, либо гораздо меньше по сравнению с ошибками  . Если же это не так, задача существенно усложняется.
. Если же это не так, задача существенно усложняется.
Относительно ошибок  предположим, что они подчиняются схеме Гаусса-Маркова [2]:
предположим, что они подчиняются схеме Гаусса-Маркова [2]:
1) центрированы, т. е. их математическое ожидание равно нулю,  (систематическая ошибка – постоянная, прогрессирующая или периодическая – отсутствует);
(систематическая ошибка – постоянная, прогрессирующая или периодическая – отсутствует);
2) гомоскедастичны, т. е. данные  равноточны, их дисперсии в разных узлах одинаковы,
равноточны, их дисперсии в разных узлах одинаковы,  ;
;
3) ошибки в разных узлах некоррелированы, т. е. 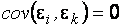 ,
,  и распределены нормально.
и распределены нормально.
Относительно неизвестной истинной зависимости 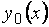 сделаем общепринятые предположения:
сделаем общепринятые предположения:
1) истинная зависимость существует в виде непрерывной дифференцируемой функции во всем диапазоне изменения аргумента, т. е.  ;
;
2) она представима в виде
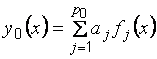 , (1.9)
, (1.9)
где  – неизвестные истинные параметры, число которых
– неизвестные истинные параметры, число которых  полагается известным, а
полагается известным, а  – известные функции (базисные функции).
– известные функции (базисные функции).
Число узлов  (все значения
(все значения  различны) должно быть
различны) должно быть 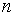 больше числа неизвестных параметров
больше числа неизвестных параметров  :
:  . Если число узлов равно числу параметров, то эмпирическая кривая пройдет по всем точкам
. Если число узлов равно числу параметров, то эмпирическая кривая пройдет по всем точкам 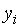 , но с истинной зависимостью, скорее всего, не будет иметь ничего общего. Если же
, но с истинной зависимостью, скорее всего, не будет иметь ничего общего. Если же  , то задача вообще неразрешима.
, то задача вообще неразрешима.
Предположим, что случайная величина  имеет нормальное распределение, т. е.
имеет нормальное распределение, т. е.  . Отсюда следует, что и случайная величина
. Отсюда следует, что и случайная величина  . Хотя многие оптимальные свойства МНК- оценок имеют место при любом законе распределения ошибок с нулевым математическим ожиданием и конечными дисперсиями, при нормальном законе распределения ошибок, появляются дополнительные оптимальные свойства. Предположение о нормальности закона распределения лежит в основе классического регрессионного анализа.
. Хотя многие оптимальные свойства МНК- оценок имеют место при любом законе распределения ошибок с нулевым математическим ожиданием и конечными дисперсиями, при нормальном законе распределения ошибок, появляются дополнительные оптимальные свойства. Предположение о нормальности закона распределения лежит в основе классического регрессионного анализа.
Это предположение на практике довольно часто выполняется, что является следствием центральной предельной теоремы теории вероятностей.
Итак, задача состоит в поиске математической модели 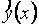 , адекватной опытным значениям. Т. е. по результатам наблюдений, искаженных ошибками, надо восстановить истинную зависимость или построить регрессионную кривую. Эта обратная задача имеет, как правило, неединственное решение. Например,
, адекватной опытным значениям. Т. е. по результатам наблюдений, искаженных ошибками, надо восстановить истинную зависимость или построить регрессионную кривую. Эта обратная задача имеет, как правило, неединственное решение. Например,  -образную кривую можно аппроксимировать параболой, кубической параболой, гиперболой, отрезком синусоиды и т.п. Таким образом, достаточно часто требуется анализировать несколько математических моделей.
-образную кривую можно аппроксимировать параболой, кубической параболой, гиперболой, отрезком синусоиды и т.п. Таким образом, достаточно часто требуется анализировать несколько математических моделей.
Последовательность этапов регрессионного анализа
Рассмотрим кратко этапы регрессионного анализа.
Формулировка задачи. На этом этапе формируются предварительные гипотезы о зависимости исследуемых явлений.
Определение зависимых и независимых (объясняющих) переменных.
Сбор статистических данных. Данные должны быть собраны для каждой из переменных, включенных в регрессионную модель.
Формулировка гипотезы о форме связи (простая или множественная, линейная или нелинейная).
Определение функции регрессии (заключается в расчете численных значений параметров уравнения регрессии)
Оценка точности регрессионного анализа.
Интерпретация полученных результатов. Полученные результаты регрессионного анализа сравниваются с предварительными гипотезами. Оценивается корректность и правдоподобие полученных результатов.
Предсказание неизвестных значений зависимой переменной.
При помощи регрессионного анализа возможно решение задачи прогнозирования и классификации. Прогнозные значения вычисляются путем подстановки в уравнение регрессии параметров значений объясняющих переменных. Решение задачи классификации осуществляется таким образом: линия регрессии делит все множество объектов на два класса, и та часть множества, где значение функции больше нуля, принадлежит к одному классу, а та, где оно меньше нуля, - к другому классу.
положительная линейная регрессия (выражается в равномерном росте функции);
положительная равноускоренно возрастающая регрессия;
положительная равнозамедленно возрастающая регрессия;
отрицательная линейная регрессия (выражается в равномерном падении функции);
отрицательная равноускоренно убывающая регрессия;
отрицательная равнозамедленно убывающая регрессия.
Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной).
http://www.machinelearning.ru/
Корреляционный анализ
http://ecsocman.hse.ru/data/437/641/1219/chap2.pdf
Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует определённое значение другой. Такой зависимостью связаны, например, радиус круга и его площадь, количество купленного товара и его стоимость, количество потребляемой абонентом электроэнергии и плата за неё и другое.
Однако часто встречаются переменные величины, которые являются зависимыми, но каждому значению одной соответствует не определённое, а некоторое множество значений другой, причём число значений и сами эти значения не отражают определённой закономерности.
Множество значений переменной y, соответствующих фиксированному значению переменной x, будем рассматривать как соответствующее ему распределение переменной y.
Переменные величины x и y связаны статистически, если каждому значению одной из них соответствует распределение другой, меняющееся с изменением первой величины и по вариантам и по частотам.
Таким образом, при корреляционной связи каждому значению аргумента соответствует не одно, а несколько значений функции и между ними нет тесной зависимости. Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и групповыми средними другой.
(y на x)   (x на y)
Уравнения, выражающие в общем виде корреляционные зависимости, называются корреляционными уравнениями или уравнениями регрессии.
Различают линейные и нелинейные регрессии.
Линейная регрессия: (x на y)
Уравнения, выражающие в общем виде корреляционные зависимости, называются корреляционными уравнениями или уравнениями регрессии.
Различают линейные и нелинейные регрессии.
Линейная регрессия: 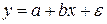 или или 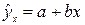 .
Нелинейные регрессии делятся на два класса:
1) регрессии, нелинейные относительно включённых в анализ объясняющих переменных, но линейные по оцениваемым параметрам:
· полиномы разных степеней: .
Нелинейные регрессии делятся на два класса:
1) регрессии, нелинейные относительно включённых в анализ объясняющих переменных, но линейные по оцениваемым параметрам:
· полиномы разных степеней:  ;
· равносторонняя гипербола: ;
· равносторонняя гипербола: 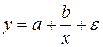 ;
2) регрессии, нелинейные по оцениваемым параметрам:
· степенная: ;
2) регрессии, нелинейные по оцениваемым параметрам:
· степенная:  ;
· показательная: ;
· показательная:  ;
· экспоненциальная: ;
· экспоненциальная:  .
В зависимости от количества факторов, включённых в уравнение регрессии, принято различать: простую (парную) и множественную регрессии.
Простая регрессия – представляет собой регрессию между двумя переменными y и x, то есть вида .
В зависимости от количества факторов, включённых в уравнение регрессии, принято различать: простую (парную) и множественную регрессии.
Простая регрессия – представляет собой регрессию между двумя переменными y и x, то есть вида  , где , где  - зависимая переменная (результативный признак); - зависимая переменная (результативный признак);  - независимая или объясняющая переменная (признак – фактор).
Множественная регрессия – представляет собой регрессию результативного признака с двумя и большим числом факторов, то есть модель вида - независимая или объясняющая переменная (признак – фактор).
Множественная регрессия – представляет собой регрессию результативного признака с двумя и большим числом факторов, то есть модель вида  .
Любое эконометрическое исследование начинается о спецификации модели, то есть с формулировки вида модели, исходя из соответствующей теории связи между переменными. То есть исследование начинается с теории, устанавливающей связь между явлениями.
Прежде всего, из всего круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.
Рассмотрим гипотезу: величина спроса y на товар А находится в обратной зависимости от цены x .
Любое эконометрическое исследование начинается о спецификации модели, то есть с формулировки вида модели, исходя из соответствующей теории связи между переменными. То есть исследование начинается с теории, устанавливающей связь между явлениями.
Прежде всего, из всего круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.
Рассмотрим гипотезу: величина спроса y на товар А находится в обратной зависимости от цены x
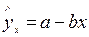 в уравнении регрессии корреляционная связь признаков представлена в виде функциональной связи, выраженной соответствующей математической функцией.
Статистические связи между переменными изучаются методами корреляционного и регрессионного анализа.
Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными.
Основной задачей корреляционного анализа – выявление связей между случайными переменными и оценка её тесноты.
в уравнении регрессии корреляционная связь признаков представлена в виде функциональной связи, выраженной соответствующей математической функцией.
Статистические связи между переменными изучаются методами корреляционного и регрессионного анализа.
Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными.
Основной задачей корреляционного анализа – выявление связей между случайными переменными и оценка её тесноты.
|
Корреляционная зависимость между х и у называется линейной, если обе линии регрессии ( а; по у и у по х) являются прямыми. [1]
Корреляционная зависимость ( correlation) - зависимость между показателями, которая проявляется лишь в общем, среднем при массовом наблюдении. [2]
Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии.
К. Система нормальных уравнений для линейной регрессии:  . Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel
. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel
Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.
см. также Корреляционная таблица.
ПРИМЕР. Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели - определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y(тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x, т. е. модель вида:
y(x) = f^(x),
где y – зависимая переменная (результативный признак); x – независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменными x и y нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина y складывается из двух слагаемых:
y = yx + ε,
где y – фактическое значение результативного признака; yx – теоретическое значение результативного признака, найденное исходя из уравнения регрессии; ε – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.
Виды нелинейной регрессии
| Вид | Класс нелинейных моделей |
1. Полиномальное уравнение регрессии: y = a + bx + cx2 (см. aa href="http://math.semestr.ru/trend/analis.php" target="_blank">метод выравнивания)
2. Гиперболическое уравнение регрессии: 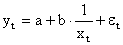 3. Квадратичное уравнение регрессии:
3. Квадратичное уравнение регрессии: 
| Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам |
1. Показательное уравнение регрессии:  2. Экспоненциальное уравнение регрессии:
2. Экспоненциальное уравнение регрессии:  3. Степенное уравнение регрессии:
3. Степенное уравнение регрессии:  4. Полулогарифмическое уравнение регрессии: y = a + b lg(x)
4. Полулогарифмическое уравнение регрессии: y = a + b lg(x)
| Нелинейные по оцениваемым параметрам |
Здесь ε - случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка - это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx2.

Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx2 + dx3.

Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
1. Замена переменных.
2. Логарифмирование обеих частей уравнения.
3. Комбинированный
. парная - регрессия между двумя переменными у и x, т. е, модель вида: у = f (x) + Е, где у -зависимая переменная (результативный признак), x – независимая, объясняющая переменная (признак - фактор), Е - возмущение, или стохастическая переменная, включающая влияние неучтенных факторов в модели
множественная - регрессия между переменными у и х1 , х2 ...xm, т. е. модель вида: у = f(х1 , х2 ...xm)+E, где у - зависимая переменная (результативный признак), х1 , х2 ...xm - независимые, объясняющие переменные (признаки-факторы), Е- возмущение или стохастическая переменная, включающая влияние неучтенных факторов в модели;
Первый этап - сбор данных.
В корреляционно-регрессионном анализе решающую роль играет качество данных, создавая фундамент прогнозам. Поэтому имеется ряд требований и правил, которые следует соблюдать.
1. Данные должны быть наблюдаемыми, т. е. полученными в результате замера, а не расчета.
2. Наблюдения следует спланировать.
3. Число наблюдений должно быть не менее чем в 5 - 6, а лучше - не менее чем в 10 раз больше числа факторов.
4. Чем больше неодинаковых (не повторяющихся) данных, и чем они однороднее, тем
лучше получится уравнение, если связи существенны.
5. Подозрительные данные до начала анализа рекомендуется отбрасывать (исключать из массива).
Второй этап - корреляционный анализ.
Целью этапа является определение характера связи между факторами, характеризующими исследуемые процессы или объекты. Связь может быть прямой или обратной, а и сила связи определена следующими качественными значениями - связь отсутствует, связь слабая, умеренная, заметная, сильная, весьма сильная, полная связь. Корреляционный анализ создает информацию о характере и степени выраженности связи (коэффициент корреляции), которая используется для отбора существенных факторов, а также для планирования эффективной последовательности расчета параметров регрессионных уравнений.
При одном факторе вычисляют коэффициент корреляции, а при наличии нескольких факторов строят корреляционную матрицу, из которой выясняют два вида связей:
- связи зависимой переменной с независимыми переменными;
- связи между самими независимыми переменными.
Рассмотрение матрицы позволяет, выявить факторы, действительно влияющие на исследуемую зависимую переменную, и выстроить (ранжировать) их по убыванию связи, а также минимизировать число факторов в модели, исключив часть факторов, которые сильно или функционально связаны с другими факторами (речь идет о связях независимых переменных между собой).
Наиболее надежными на практике бывают одно- и двухфакторные модели.
Если будет обнаружено, что два фактора имеют сильную или полную связь между собой, то в регрессионное уравнение достаточно будет включить один из них. Например, в одно регрессионное уравнение нельзя одновременно включать переменные «Количество работающих» и «Производительность труда» как независимые (поскольку показатель производительности труда получают делением выработки работников на количество работающих).
Третий этап - расчет параметров и построение регрессионных моделей.
На этом этапе необходимо отыскать наиболее точную меру выявленной связи, для того чтобы можно было прогнозировать, предсказывать значения зависимой величины Y, если будут известны значения независимых величин X1, X2, …..Xn
Эта мера обобщенно выражается математической моделью линейной множественной регрессионной зависимости
Y = a 0 + a1X1 + a 2X2 + . . . . . + a nXn ,
где
a 0 - свободный член (константа, или пересечение);
a1 , a 2 , ………a n - коэффициенты регрессии;
X1 , X2 ,……... Xn - факторы или предикаты.
Осуществление третьего этапа сильно зависит от выводов, которые получены при анализе корреляционной матрицы. Можно значительно ускорить проведение регрессионного анализа и снизить затраты на исследование, если принять правильную стратегию поиска наилучшего уравнения. Для этого необходимо знать основные и наиболее эффективные методы поиска наилучшего уравнения.
После получения каждого варианта уравнения обязательной процедурой является оценка его статистической значимости, поскольку главная цель - получить уравнение наивысшей значимости, поэтому третий этап корреляционно-регрессионного анализа неразрывно связан с четвертым.
Четвертый этап – определение статистической значимости модели.
Проверяется пригодность модели для использования ее в целях предсказания значений зависимой величины Y. Для оценки качества полученной модели необходимо вычислить ряд коэффициентов, сравнить их с известными статистическими критериями и оценить модель с точки зрения здравого смысла.
На этом этапе исключительно важную роль играют коэффициент детерминации, F-критерий (критерий Фишера), t – статистики (критерий Стьюдента).
Коэффициент детерминации (R2) - это квадрат множественного коэффициента корреляции между наблюдаемым значением Y и его теоретическим значением, вычисленным на основе модели с определенным набором факторов. Коэффициент' детерминации может принимать значения от 0 до 1. Эта величина особенно полезна для сравнения ряда различных моделей и выбора наилучшей модели.
R2 есть доля вариации прогнозной (теоретической) величины Y относительно наблюденных значений Y, объясненная за счет включенных в модель факторов. Очень хорошо, если R2 > = 80%. Это значит, что на 80% теоретические значения Y зависят от рассматриваемых факторов, а на 20% от других, не участвовавших в модели факторов. Для увеличения коэффициента детерминации необходимо выявить новые факторы, включить их в уравнение регрессии и определить R2 .
Вторым коэффициентом является F-критерий значимости регрессии для уравнения в целом. Это рассчитанное по наблюденным данным значение следует сравнивать с соответствующим критическим значением Fк , которое выбирает из статистических таблиц на заданном уровне вероятности (на том, на каком вычислялись параметры модели, например, 95%).
Если наблюденное значение F окажется меньше критического значения Fк, то уравнение нельзя считать статистически значимым, а модель не адекватна исследуемому процессу и не может быть использована для целей прогнозирования.
t – статистики позволяют оценить статистическую значимость каждого фактора модели, что дает возможность определить, какая переменная должна быть исключена на текущем шаге построения уравнения регрессии. Аналогично F-критерию, вычисленные t – статистики сравниваются с критическим значением критерия Стьюдента, определенным по статистическим таблицам.
Четвертый этап – использование модели.
Если полученная модель статистически значима, ее применяют для прогнозирования (предсказания), управления или объяснения.
Если же обнаружена незначимость, то модель отвергается, предполагая, что истинной окажется какая-то другая форма связи, которую надо найти.
На пятом этапе осуществляется прогноз возможных значений результата по лучшим значениям факторных признаков, включенных в модель. Здесь выбираются наилучшие и наихудшие значения факторов и результата.
https://books.google.ru/books?id=Rgc_qP5CwsMC&pg=PA40&lpg=PA40&dq=Экономический+анализ+на+основе+уравнений+регрессии&source=bl&ots=dE3mur2xwr&sig=ZApMG9fJXhggOAWo1GfxzO_M2lE&hl=ru&sa=X&redir_esc=y#v=onepage&q=%D0%AD%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9%20%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%20%D0%BD%D0%B0%20%D0%BE%D1%81%D0%BD%D0%BE%D0%B2%D0%B5%20%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B9%20%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D0%B8&f=false
|
из
5.00
|
Обсуждение в статье: Одноканальная СМО с отказами |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

