 |
Главная |
Одноканальная СМО с ожиданием и неограниченной очередью
|
из
5.00
|
Многоканальная СМО с отказами
В подавляющем большинстве случаев на практике система массового обслуживания является многоканальными, то есть параллельно могут обслуживаться несколько заявок, и, следовательно,модели с обслуживающими каналами (где число каналов обслуживания n>1) представляют несомненный интерес.
Процесс массового обслуживания, описываемый данной моделью, характеризуется интенсивностью входного потока λ, при этом параллельно может обслуживаться не более n клиентов (заявок). Средняя продолжительность обслуживания одной заявки равняется 1/μ. Режим функционирования того или иного обслуживающего канала не влияет на режим функционирования других обслуживающих каналов системы, при чем длительность процедуры обслуживания каждым из каналов является случайной величиной, починенной экспоненциальному закону распределения. Конечная цель использования параллельно включенных обслуживающих каналов заключается в повышение (по сравнению с одноканальной системой) скорости обслуживания требований за счет обслуживания одновременно n клиентов.
Стационарное решение системы имеет вид:
 ;
;
где  ,
,  .
.
Формулы для вычисления вероятностей называются формулами Эрланга.
Определим вероятностные характеристики функционирования многоканальной СМО с отказами в стационарном режиме:
вероятность отказа:
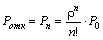 .
.
так как заявка получает отказ, если приходит в момент, когда все каналов заняты. Величина Ротк характеризует полноту обслуживания входящего потока;
вероятность того, что заявка будет принята к обслуживанию (она же – относительная пропускная способность системы) дополняет Ротк до единицы:
 .
.
абсолютная пропускная способность

среднее число каналов, занятых обслуживанием (  ) следующее:
) следующее:

Величина  характеризует степень загрузки СМО.
характеризует степень загрузки СМО.
Одноканальная СМО с ожиданием и неограниченной очередью
Перейдем теперь к рассмотрению одноканальной СМО с ожиданием без ограничения на вместимость блока ожидания (т.е. Ν → ∞ ). Остальные условия функционирования СМО остаются без изменений.
Устойчивое решение в такой системе существует только тогда, когда λ<μ, то есть заявки должны обслуживаться с большей скоростью, чем поступают, в противном случае очередь может разрастись до бесконечности.
Вероятность того, что в системе находится п заявок, вычисляется по формуле
Pn=(1-r)rn, n=0,1,2,…,
где r = λ/μ <1.
Характеристики одноканальной СМО с ожиданием, без ограничения на длину очереди, следующие:
среднее число находящихся в системе клиентов (заявок) на обслуживание:

средняя продолжительность пребывания клиента в системе:
 ;
;
среднее число клиентов в очереди на обслуживание:
Lq=LS -  ;
;
средняя продолжительность пребывания клиента в очереди:
Wq=  ;
; 
|
из
5.00
|
Обсуждение в статье: Одноканальная СМО с ожиданием и неограниченной очередью |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

