 |
Главная |
Алгоритм решения уравнения в полных дифференциалах
|
из
5.00
|
1. Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах, используя необходимое и достаточное условие:
∂Q∂x=∂P∂y.
2. Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u(x,y):
⎧⎩⎨∂u∂x=P(x,y)∂u∂y=Q(x,y).
3. Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:
u(x,y)=∫P(x,y)dx+φ(y).
4. Дифференцируя по переменной y, подставим функцию u(x,y) во второе уравнение:
∂u∂y=∂∂y[∫P(x,y)dx+φ(y)]=Q(x,y).
Отсюда получаем выражение для производной неизвестной функции φ(y):
φ′(y)=Q(x,y)−∂∂y(∫P(x,y)dx).
5. Интегрируя последнее выражение, находим функцию φ(y) и, следовательно, функцию u(x,y):
u(x,y)=∫P(x,y)dx+φ(y).
6. Общее решение уравнения в полных дифференциалах записывается в виде:
u(x,y)=C.
Примечание: На шаге 3, вместо интегрирования первого уравнения по переменной x, мы можем проинтегрировать второе уравнение по переменной y. После интегрирования нужно определить неизвестную функцию ψ(x).
Второй закон Ньютона — дифференциальный закон механического движения, описывающий зависимость ускорения тела от равнодействующей всех приложенных к телу сил и массы тела. Один из трёх законов Ньютона.
Объектом, о котором идёт речь во втором законе Ньютона, является материальная точка, обладающая неотъемлемым свойством — инертностью, величина которой характеризуется массой. В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и не зависящей от каких-либо особенностей её движения и взаимодействия с другими телами[1][2][3][4].
Второй закон Ньютона в его наиболее распространённой формулировке утверждает: в инерциальных системах ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению иобратно пропорционально массе материальной точки.
В приведённой формулировке второй закон Ньютона справедлив только для скоростей, много меньших скорости света, и в инерциальных системах отсчёта.
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
Обычно этот закон записывается в виде формулы:

где  — ускорение тела,
— ускорение тела, 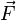 — сила, приложенная к телу, а
— сила, приложенная к телу, а 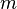 — масса материальной точки.
— масса материальной точки.
Или в ином виде:
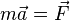
- Формулировка второго закона Ньютона с использованием понятия импульса:
В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на неё силе[6].

где  — импульс (количество движения) точки,
— импульс (количество движения) точки,  — её скорость, а
— её скорость, а 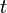 — время.
— время.
При такой формулировке, как и ранее, полагают, что масса материальной точки неизменна во времени[7][8][9].
Иногда в рамках классической механики предпринимались попытки распространить сферу применения уравнения  и на случай тел переменной массы. Однако вместе с таким расширительным толкованием уравнения приходилось существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила[10][11].
и на случай тел переменной массы. Однако вместе с таким расширительным толкованием уравнения приходилось существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила[10][11].
Уравнения, соответствующие данному закону, называются уравнениями движения материальной точки.
При независимом выборе единиц массы, силы и ускорения выражение второго закона нужно писать в виде

Линейное уравнение первого порядка в стандартной записи имеет вид:

Что мы видим?
1) В линейное уравнение входит первая производная  .
.
2) В линейное уравнение входит произведение  , где
, где  – одинокая буковка «игрек» (функция), а
– одинокая буковка «игрек» (функция), а  – выражение, зависящее только от «икс».
– выражение, зависящее только от «икс».
3) И, наконец, в линейное уравнение входит выражение  , тоже зависящее только от«икс». В частности,
, тоже зависящее только от«икс». В частности,  может быть константой.
может быть константой.
Примечание: Разумеется, в практических примерах эти три слагаемых не обязаны располагаться именно в таком порядке, их спокойно можно переносить из части со сменой знака.
Перед тем, как перейти к практическим задачам, рассмотрим некоторые частные модификации линейного уравнения.
– Как уже отмечалось, выражение  может быть некоторой константой
может быть некоторой константой  (числом), в этом случае линейное уравнение принимает вид:
(числом), в этом случае линейное уравнение принимает вид: 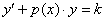
– Выражение  тоже может быть некоторой константой
тоже может быть некоторой константой  , тогда линейное уравнение принимает вид:
, тогда линейное уравнение принимает вид:  . В простейших случаях константа равна +1 или –1, соответственно, линейное уравнение записывается еще проще:
. В простейших случаях константа равна +1 или –1, соответственно, линейное уравнение записывается еще проще:  или
или  .
.
– Рядом с производной может находиться множитель  , зависящий только от «икс»:
, зависящий только от «икс»:  – это тоже линейное уравнение.
– это тоже линейное уравнение.
Поехали.
Пример 1
Решить дифференциальное уравнение 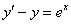
Решение: Данное уравнение является линейным и имеет простейший вид:  .
.
|
из
5.00
|
Обсуждение в статье: Алгоритм решения уравнения в полных дифференциалах |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

