 |
Главная |
Дифференциальные уравнения высших порядков
|
из
5.00
|
- Дифференциальные уравнения, допускающие понижение порядка.
Порядок дифференциального уравнения  , которое не содержит искомой функции и ее производных до k-1 порядка, может быть понижен до n-k заменой
, которое не содержит искомой функции и ее производных до k-1 порядка, может быть понижен до n-k заменой 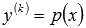 .
.
В этом случае 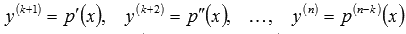 , и исходное дифференциальное уравнение сведется к
, и исходное дифференциальное уравнение сведется к  . После нахождения его решения p(x) останется вернуться к замене
. После нахождения его решения p(x) останется вернуться к замене 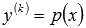 и определить неизвестную функцию y.
и определить неизвестную функцию y.
Например, дифференциальное уравнение 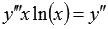 после замены
после замены 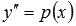 станет уравнением с разделяющимися переменными
станет уравнением с разделяющимися переменными 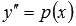 , и его порядок с третьего понизится до первого.
, и его порядок с третьего понизится до первого.
Если дифференциальное уравнение не содержит аргумента x, то есть, имеет вид  , то его порядок может быть снижен на единицу заменой
, то его порядок может быть снижен на единицу заменой 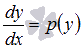 , где p(y(x)) будет сложной функцией. Тогда по правилу дифференцирования сложной функции получим
, где p(y(x)) будет сложной функцией. Тогда по правилу дифференцирования сложной функции получим
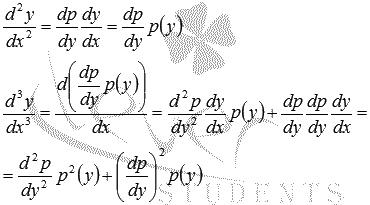
и так далее.
Подставив эти результаты в исходное уравнение, получаем дифференциальное уравнение не единицу меньшего порядка.
К примеру, дифференциальное уравнение 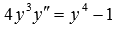 заменой
заменой 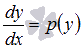 приводится к уравнению с разделяющимися переменными
приводится к уравнению с разделяющимися переменными 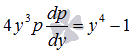 .
.
Подробное решение подобных примеров представлено в статьедифференциальные уравнения, допускающие понижения порядка.
- Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами
 и
и  .
.
Чтобы определить общее решение таких видов дифференциальных уравнений, во-первых, требуется найти корни характеристического уравнения 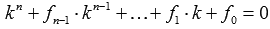 . В этом Вам может помочь статьярешение уравнений высших степеней. Далее, отталкиваясь от значений корней характеристического уравнения, общее решение ЛОДУ
. В этом Вам может помочь статьярешение уравнений высших степеней. Далее, отталкиваясь от значений корней характеристического уравнения, общее решение ЛОДУ 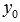 записывается в стандартной форме, а общее решение неоднородного уравнения представляется суммой
записывается в стандартной форме, а общее решение неоднородного уравнения представляется суммой 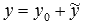 , где
, где 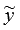 - частное решение неоднородного дифференциального уравнения.
- частное решение неоднородного дифференциального уравнения. 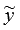 можно определить методом вариации произвольных постоянных.
можно определить методом вариации произвольных постоянных.
В качестве примера ЛНДУ с постоянными коэффициентами приведем 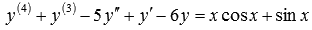 , ему соответствует ЛОДУ
, ему соответствует ЛОДУ 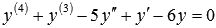 .
.
Подробное описание теории и детальный разбор решения примеров смотрите в разделе линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами.
- Линейные однородные и неоднородные дифференциальные уравнения высших порядков
 и
и  .
.
Общее решение ЛНДУ высших порядков ищется в виде 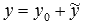 , где
, где 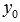 - общее решение соответствующего ЛОДУ, а
- общее решение соответствующего ЛОДУ, а 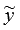 - частное решение неоднородного дифференциального уравнения.
- частное решение неоднородного дифференциального уравнения.
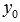 представляет собой линейную комбинацию линейно независимых функций
представляет собой линейную комбинацию линейно независимых функций 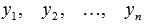 , каждая из которых является частным решением ЛОДУ, то есть, обращает равенство
, каждая из которых является частным решением ЛОДУ, то есть, обращает равенство 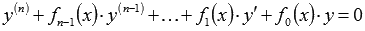 в тождество. Частные решения
в тождество. Частные решения 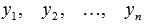 обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.
обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.
Когда общее решение линейного однородного дифференциального уравнения найдено, частное решение соответствующего неоднородного уравнения можно определить методом вариации произвольных постоянных.
Итак, 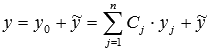 .
.
Краткое описание теории приведено в статье линейные дифференциальные уравнения высших порядков.
К началу страницы
Системы дифференциальных уравнений вида 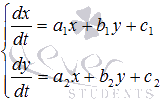
Обыкнове́нные дифференциа́льные уравне́ния (ОДУ) — это дифференциальные уравнения для функции от одной переменной. (Этим оно отличается от уравнения в частных производных, где неизвестная — это функция нескольких переменных.) Таким образом, ОДУ — это уравнения вида
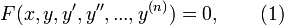
где 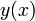 — неизвестная функция (возможно, вектор-функция, тогда
— неизвестная функция (возможно, вектор-функция, тогда 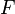 , как правило, тоже вектор-функция со значениями в пространстве той же размерности; в этом случае говорят о системе дифференциальных уравнений), зависящая от независимой переменной
, как правило, тоже вектор-функция со значениями в пространстве той же размерности; в этом случае говорят о системе дифференциальных уравнений), зависящая от независимой переменной 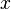 , штрих означает дифференцирование по
, штрих означает дифференцирование по 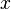 . Число
. Число 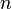 (порядок старшей производной, входящей в данное уравнение) называется порядком дифференциального уравнения (1).
(порядок старшей производной, входящей в данное уравнение) называется порядком дифференциального уравнения (1).
Независимая переменная 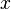 часто интерпретируется (особенно в дифференциальных уравнениях, возникающих в физических и других естественно-научных задачах) как время, поэтому её часто обозначают буквой
часто интерпретируется (особенно в дифференциальных уравнениях, возникающих в физических и других естественно-научных задачах) как время, поэтому её часто обозначают буквой 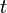 . Переменная
. Переменная 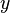 — некоторая величина (или совокупность величин, если
— некоторая величина (или совокупность величин, если 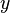 является вектор-функцией), изменяющаяся со временем. Например,
является вектор-функцией), изменяющаяся со временем. Например, 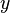 может означать набор координат точки в пространстве; в этом случае уравнение (1) описывает движение точки в пространстве, то есть изменение её координат с течением времени. Независимая переменная
может означать набор координат точки в пространстве; в этом случае уравнение (1) описывает движение точки в пространстве, то есть изменение её координат с течением времени. Независимая переменная 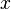 обычно принимает вещественные значения, однако рассматриваются и дифференциальные уравнения, в которых переменная
обычно принимает вещественные значения, однако рассматриваются и дифференциальные уравнения, в которых переменная 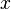 комплексная (так называемые уравнения с комплексным временем).
комплексная (так называемые уравнения с комплексным временем).
Наиболее часто встречаются дифференциальные уравнения вида
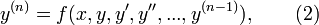
в которых старшая производная 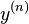 выражается в виде функции от переменных
выражается в виде функции от переменных 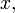
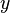 и производных
и производных 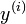 порядков меньше
порядков меньше 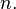 Такие дифференциальные уравнения называются нормальными или разрешёнными относительно производной.
Такие дифференциальные уравнения называются нормальными или разрешёнными относительно производной.
В противоположность уравнениям вида (2), дифференциальные уравнения вида (1) называются уравнениями, не разрешёнными относительно производной или неявными дифференциальными уравнениями.
Классическим решением дифференциального уравнения (2) называется 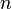 раз дифференцируемая функция
раз дифференцируемая функция 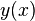 , удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительное условие. Начальным условием для уравнения (2) называется условие
, удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительное условие. Начальным условием для уравнения (2) называется условие
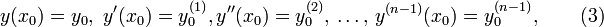
где 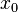 — некоторое фиксированное значение независимой переменной (фиксированный момент времени), а
— некоторое фиксированное значение независимой переменной (фиксированный момент времени), а 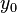 и
и 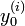 — соответственно, фиксированные значения функции
— соответственно, фиксированные значения функции 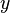 и всех её производных до порядка
и всех её производных до порядка 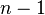 включительно. Дифференциальное уравнение (2) вместе с начальным условием (3) называется начальной задачей или задачей Коши:
включительно. Дифференциальное уравнение (2) вместе с начальным условием (3) называется начальной задачей или задачей Коши:
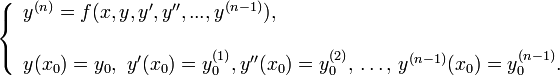
При достаточно общих ограничениях на функцию 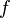 , стоящую в правой части уравнения (2), задача Коши для этого уравнения имеет единственное решение, определённое на некотором интервале оси времени
, стоящую в правой части уравнения (2), задача Коши для этого уравнения имеет единственное решение, определённое на некотором интервале оси времени 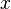 , содержащем начальное значение
, содержащем начальное значение 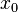 (этот интервал, вообще говоря, может не совпадать со всей осью).
(этот интервал, вообще говоря, может не совпадать со всей осью).
Основные задачи и результаты теории дифференциальных уравнений: существование и единственность решения различных задач для ОДУ, методы решения простейших ОДУ, качественное исследование решений ОДУ без нахождения их явного вида.
https://ru.wikipedia.org/wiki/Обыкновенное_дифференциальное_уравнение
Итак, требуется решить дифференциальное уравнение:
Действие первое. Пожалуйста, забудьте задачку про частные производные и готовый ответ. Дело в том, что когда вам предложен для решения произвольный диффур, то вы ещё не знаете о том, что это уравнение в полных дифференциалах. И данный факт крайне желательно доказать в самом начале решения.
Докажем, что уравнение является уравнением в полных дифференциалах. Как это сделать? Уравнение в полных дифференциалах имеет вид . Вспоминаем характерное и очень удобное равенство смешанных производных второго порядка: . Вот его и надо проверить:
, значит, данное уравнение является уравнением в полных дифференциалах.
На чистовике проверка проводится немного не так. Мы не имеем права использовать букву , так как изначально не знаем, является ли данное уравнение полным дифференциалом некоторой функции . А вдруг не является? Тогда вышеприведенные записи с буквой будут некорректны с математической точки зрения. Поэтому обычно используют нейтральные буквы «пэ» и «ку», а сама проверка на чистовике выглядит примерно так:
“
Проверим, является ли уравнение уравнением в полным дифференциалах:
, значит, данное ДУ является уравнением в полных дифференциалах
”
Вот только теперь, после доказательства, мы можем использовать букву «эф», поскольку показано, что дифференциальное уравнение является полным дифференциалом некоторой функции и имеет вид:
Ну, а коль скоро уравнение имеет вид , то:
Таким образом, нам известны две частные производные, и наша задача состоит в том, чтобы восстановить общий интеграл .
Существуют два зеркальных способа решения. В статье я остановлюсь на более привычном способе решения, но в конце рассмотрю и второй зеркальный вариант, он не менее важен.
Действие второе. Работаем с верхней производной . Нижнюю производную пока запишем на листочек и спрячем в карман.
Если дана частная производная , то нужная нам функция восстанавливается с помощью обратного действия – частного интегрирования:
Когда мы берём интеграл по «икс», то переменная «игрек» считается константой. Как видите, принцип точно такой же, как и при нахождении частных производных.
Я запишу подробно, сначала используем свойства линейности интеграла:
Еще раз подчеркиваю, что «игрек» в данном случае является константой и выносится за знак интеграла (т.е. не участвует в интегрировании).
В итоге:
Здесь – некоторая, пока ещё неизвестная функция, зависящая только от «игрек».
Правильно ли вычислен интеграл? В этом легко убедиться, если выполнить проверку, т.е. найти частную производную:
– получена исходная подынтегральная функция.
Надеюсь всем, понятно, почему . Функция зависит только от «игрек», а, значит, является константой.
Действие третье.
Берем «недоделанный» результат и дифференцируем его по «игрек»:
Функцию мы пока не знаем, но производная-то по «игрек» у неё существует, поэтому запись – совершенно законна.
Действие четвертое.
Перепишем результат предыдущего пункта:
А теперь достаем из широких штанин листочек с производной:
Приравниваем:
И сокращаем всё, что можно сократить:
Находим функцию , для этого необходимо взять интеграл от правой части:
Заключительный аккорд: Подставим найденную функцию в «недоделанный» результат :
Ответ: общий интеграл:
Проверка уже выполнена в самом начале урока – находим частные производные первого порядка и составляем полный дифференциал, в результате должно получиться исходное дифференциальное уравнение.
Второй способ проверки состоит в том, чтобы найти производную от функции, заданной неявно:
Дифференциальное уравнение вида
P(x,y)dx+Q(x,y)dy=0
называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y) с непрерывными частными производными, что справедливо выражение
du(x,y)=P(x,y)dx+Q(x,y)dy.
Общее решение уравнения в полных дифференциалах определяется формулой
u(x,y)=C,
где C − произвольная постоянная.
|
из
5.00
|
Обсуждение в статье: Дифференциальные уравнения высших порядков |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

