 |
Главная |
Лекция 4. Синтез схем СДНФ, СКНФ, МДНФ, МКНФ
|
из
5.00
|
Синтез схем СДНФ СКНФ МДНФ МКНФ
Совершенная коньюнкция нормальной формы. СКНФ (умножение между скобками) сложение в скобках.
Совершенная коньюнкция нормальной формы СКНФ состоит из нескольких конъюнкций обеспечивающих на выходе каждой из них сигнал 0
Синтез схем СДНФ СКНФ
Под синтезом схем понимают разработку (проектирование) схем. Перед началом синтеза формулируется задача которую должна решать схема.
Техническое задание:
Назначаются входные переменные А, В, С
Назначаются выходные переменные Z, Y, X, Q, Q1
Задаются условия при которых переменные равны 1 или 0
Опираясь на эти условия создается таблица истинности. Таблица истинности однозначно определяет как будет работать проектируемая схема.
Определяются логические операции необходимые для реализации таблицы истинности
Упрощаются полученные логические выражения
Получаемые логические выражения приводят к общепринятому стандарту (нормальной форме)
Под полной конъюнкцией понимают операцию логического умножения в которой учувствуют все имеющиеся переменные или их инвертированные значения.
Количество единичных состояний в выходном столбце таблицы истинности равно количеству полных конъюнкций нормальной формы ИЛИ. Если в рассмотренном варианте таблицы истинности переменная принимает значение 0 то в соответствующей полной конъюнкции она инвертируется если 1 то не инвертируется При нескольких полных конъюнкциях нормальная форма ИЛИ получается посредством логического сложения ИЛИ полных конъюнкций. Нормальная форма ИЛИ представляет информационное содержание таблицы истинности в виде уравнения алгебры логики.
Совершенная дизъюнкция нормальной формы СДНФ состоит из нескольких конъюнкций обеспечивающих на выходе каждой из них сигнал 1


Нормальная дизъюнктивная форма (сложение между скобками) умножение в скобках.
y=(x1^x2^x3)v(  …………v
…………v 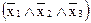
| Х1 (А) | Х2 (В) | Х3 (С) | Y | Y выражение |
| Ā^B^C | ||||
| A^B^C | ||||
Любую булеву функцию можно представить либо в виде таблицы истинности, либо в виде алгебраического уравнения. В алгебраической форме функцию удобно преобразовывать, например, с целью ее минимизации, т.е. получения наиболее простой формы. Существуют две формы функций в алгебраическом виде, называемые нормальными.
Первая форма – дизъюнктивная нормальная форма, представляет собой логическую сумму элементарных логических произведений, в каждое из которых аргумент или его отрицание входит не более одного раза. Например:

Если каждое слагаемое содержит все переменные или их отрицания, имеем первую стандартную форму или совершенную дизъюнктивную форму. Например:

Вторая форма или конъюнктивная нормальная форма есть логическое произведение элементарных логических сумм. Если каждая сумма содержит все переменные или их отрицания, имеем вторую стандартную форму или совершенную конъюнктивную форму. Например:

При переходе от таблицы к алгебраической записи всегда получается первая или вторая стандартные формы, однако, после преобразований форма записи может быть произвольной.
Переход от таблицы истинности к первой стандартной форме осуществляется следующим образом. Для каждого набора аргументов, на котором функция равна единице, записывается произведение всех аргументов, причем, если аргумент в этом наборе принимает значение 0, то пишется его отрицание. Затем производится логическое сложение этих элементарных произведений.
Для наглядности рассмотрим две функции ИЛИ и И. Их таблицы истинности представлены ниже.
| Функция ИЛИ | Функция И | ||||
| х1 | х2 | F(x1,x2) | x1 | x2 | F(x1,x2) |
Уравнение в первой стандартной форме для функции ИЛИ:
 (3.1)
(3.1)
Для функции И:
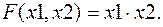 (2)
(2)
Иногда эту процедуру называют составлением структурной формулы по единицам.
Для перехода ко второй стандартной формуле необходимо:
Для каждого набора аргументов, на котором функция равна 0, составить элементарную сумму, причем если аргумент в этом наборе принимает значение 1, то пишется его отрицание. Затем эти элементарные суммы объединяются операцией логического умножения.
Уравнение во второй стандартной форме для функции ИЛИ:
 (3)
(3)
Для функции И:
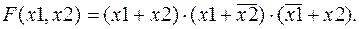 (3.4)
(3.4)
Уравнения 2 и 3 не требуют преобразований. Это их минимальная форма. Уравнения 1 и 4 могут быть преобразованы. уравнения 1 и 3, 2 и 4 записаны соответственно для функции ИЛИ и И, следовательно, должны быть тождественными:


Пользуясь теоремами булевой алгебры преобразуем уравнение 3.1. Воспользуемся правилом повторения  , правилом отрицания
, правилом отрицания 

Для преобразования уравнения 4 применим к нему принцип двойственности:
Если 
то 
И далее, аналогично предыдущему:

Еще раз применим принцип двойственности и получим окончательно:
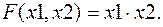
Процедура построения схемы по заданному уравнению достаточно проста. Схема строится в той же последовательности, как происходит вычисление функции. Необходимо учитывать приоритет операций: отрицание, умножение, сложение. Схема должна иметь столько входов, сколько у функции аргументов, и один выход, соответствующий самой функции. На входы подаются сигналы, соответствующие аргументам. Если кроме аргументов в уравнении есть отрицания аргументов, то для их получения в схеме применяют элементы НЕ. Для умножения используются элементы И, для сложения – ИЛИ. Для примера построим схемы по уравнениям 1 и 4.
Схема по уравнению 1:
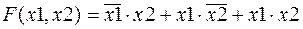
(рис. 3.1а) будет состоять из двух элементов НЕ для получения отрицаний 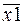 и
и  , трех двухвходовых элементов И для реализации произведений аргументов
, трех двухвходовых элементов И для реализации произведений аргументов 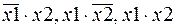 и одного трехвходового элемента ИЛИ для получения окончательной суммы трех произведений. Схема по уравнению 4:
и одного трехвходового элемента ИЛИ для получения окончательной суммы трех произведений. Схема по уравнению 4:

(рис. 3.1 б) будет состоять из двух элементов НЕ, трех элементов ИЛИ и одного элемента И.

Рис. 3.1 . Схемы построенные по уравнению 1 (а) и 4 (б)
Пример 3.1
Условие наличия сигналов на двух входах из трех и и сигнала на трех входах описывается следящей таблицей истинности.
| Х1 (А) | Х2 (В) | Х3 (С) | Y | Y выражение |

| ||||

| ||||

| ||||
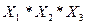
| ||||
Закон управления будет описываться как выражение вида

Совершенная дизъюнкция нормальной формы. СДНФ
Для построения той же задачи можно использовать обратное условие то есть если хотя бы два элемента неисправны то устройство не работоспособно
В этом случае определяющими будут нули взятые из таблицы истинности и если хотя бы одна из групп слагаемых не будет положительно объект будет исправным при наличии всех нулей на выходе будет ноль говорящий о неисправности блока.

Достоинством метода СДНФ СКНФ является простота построения решений
Подобный подход применяется для решения задачи диагностики алгебраическим методом при поиске алгоритма проверки исправности устройства.
|
из
5.00
|
Обсуждение в статье: Лекция 4. Синтез схем СДНФ, СКНФ, МДНФ, МКНФ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

