 |
Главная |
Определение оценок параметров экспоненциального закона
|
из
5.00
|
Оценка параметра распределения, л, находится по формуле:
л =1/  (3.3)
(3.3)
где  - оценка математического ожидания выборки.
- оценка математического ожидания выборки.
Определение оценок параметров нормального закона
Оценка параметра mt, представляющего собой среднее значение случайной величины t, равна оценке математического ожидания выборки.
Оценка параметра σ равна оценке среднего квадратического отклонения выборки.
Определение оценок при логарифмически – нормальном законе
Распределения случайной величины
Параметр µ при логарифмически–нормальном законе распределения вычисляется по формуле:
 (3.4)
(3.4)
Параметр среднего квадратического отклонения S вычисляется по формуле:
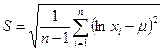 (3.5)
(3.5)
В случае больших выборок параметр µ вычисляется по формуле:
 (3,6)
(3,6)
Параметр S вычисляется по формуле:
 (3.7)
(3.7)
Задача 6
Пользуясь логарифмически-нормальным законом распределения случайной величины найти среднеквадратичное отклонение исправного состояния рулевого управления, и разжимных кулаков ножных тормозов автомобилей российского производства, если в результате наблюдения автобуса «Autosan» были получены:
– 15 значений времени исправного состояния рулевого управления  в тыс. км пробега [1,2]:
в тыс. км пробега [1,2]:
13, 27, 19, 23, 58, 32, 39, 51, 38, 47, 33, 55, 57, 59 и 45.
– 45 значений наработков на отказ разжимных кулаков в тыс. км:
251,7 201,4 177,9 70,0 198,9 133,5 125,0 290,6 173,2 218,5 234,0 287,3 220,3 144,3 243,5 167,6 250,8 217,1 102,1 199,2 246,6 163,6 175,2 205,2 329,9 308,0 177,7 209,6 221,4 165,6 165,1 218,3 221,0 145,6 300,0 197,6 246,0 139,9 174,3 219,5 236,1 223,8 244,8 160,0 118,7
Исходные данные в соответствие с вариантом принять по табл.8 исходя из соотношения  , где а– поправочный коэффициент
, где а– поправочный коэффициент
Исходные данные
Таблица 8
| Параметр | вариант | |||||||||||||||||||
| а | 0,77 | 0,78 | 0,79 | 0,80 | 0,81 | 0,82 | 0,83 | 0,84 | 0,85 | 0,86 | 0,87 | 0,88 | 0,89 | 0,90 | 0,91 | 0,92 | 0,93 | 0,94 | 0,95 | 0,96 |
Пример решения
Определить оценки параметров логарифмически-нормального закона для автобуса «Autosan» из задачи 1.
Найти оценку параметра распределения µ с помощью формулы (3.4):

Оценку параметра среднеквадратичного отклонение исправного состояния рулевого управления S найти с помощью формулы (3.5). На практике, для облегчения расчетов, используют соотношения задачи 1. Таким образом, оценку дисперсии проще найти по формуле:
 =
=
= 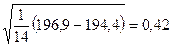
Определить оценки параметров логарифмически-нормального закона для разжимных кулаков ножных тормозов, из примера 2.
Найти оценку параметра µ с помощью формулы (3.6):

Определить количество интервалов группирования k при заданном количестве наблюдений n по формуле Стенжерса (2.6):

Величина интервала группирования может быть определена:
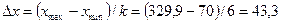
Середина интервала группирования: 
Упорядочить значения наработок на отказ в порядке возрастания и полученные параметры свести в таблицу 9
70,0 102,1 118,7 125,0 133,5 139,9 144,3 145,6 160,0 163,6 165,1 165,6 167,6 173,2 174,3 175,2 177,7 177,9 197,6 198,9 199,2 201,4 205,2 209,6 217,1 218,3 218,5 219,5 220,3 221,0 221,4 223,8 234,0 236,1 243,5 244,8 246,0 246,6 250,8 251,7 287,3 290,6 300,0 308,0 329,9
Таблица 9
| Номер интервала | Границы интервалов | Середина интервала, Xj | Число попаданий, mj |
| 70 - 113,3 | 91,7 | ||
| 113,3 - 156,6 | |||
| 156,6 - 200 | 178,3 | ||
| 200 - 243,3 | 221,7 | ||
| 243,3 - 286,6 | |||
| 286,6 - 329,9 | 308,3 |
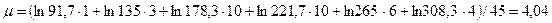
Найти оценку параметра S по формуле (3.7):

 1,9
1,9
|
из
5.00
|
Обсуждение в статье: Определение оценок параметров экспоненциального закона |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

