 |
Главная |
Проверка с помощью критерия Пирсона
|
из
5.00
|
Основным преимуществом этого критерия является то, что он может быть использован для проверки допущения о любом распределении, даже в случае, если не известны значения параметров распределения. Главный недостаток критерия - его нечувствительность к обнаружению адекватной модели, когда число наблюдений невелико. На практике при применении критерия Пирсона необходимо, чтобы число наблюдений, попавших в интервал, было не менее пяти. Если на какой то интервал попадает менее пяти значений, его объединяют с соседним.
Применение критерия Пирсона  является эффективно при числе результатов наблюдений n > 30. Поскольку в каждом интервале должно быть не менее восьми значений случайной величины.
является эффективно при числе результатов наблюдений n > 30. Поскольку в каждом интервале должно быть не менее восьми значений случайной величины.
В случае, когда значения параметров распределения определены, (задачи 2,5) эмпирические частоты попадания исходных данных в интервал  сопоставляются с частотами, вычисленными по теоретическому уравнению плотности распределения вероятностей m'j, вычисляемые по формуле:
сопоставляются с частотами, вычисленными по теоретическому уравнению плотности распределения вероятностей m'j, вычисляемые по формуле:
mj' = n·fj·Δx (4.1)
где n – объём выборки; fj – плотность распределения вероятностей, вычисленная по теоретическому уравнению плотности распределения принятого закона для середины каждого интервала.
Функция плотности распределения вероятностей на каждом интервале определяется [6,7] по теоретическому уравнению.

Критерий Пирсона записывается в виде следующего уравнения:
 (4,2)
(4,2)
где  вычисляется по формуле
вычисляется по формуле
 , (4.3)
, (4.3)
k – число степеней свободы.
Полученное значение  сравнивают с критическим значением
сравнивают с критическим значением  этого критерия. Значение
этого критерия. Значение  выбирают по таблице 1 приложения 3 в зависимости от уровня значимости а и числа степеней свободы k = r – 1, где r – число интервалов.
выбирают по таблице 1 приложения 3 в зависимости от уровня значимости а и числа степеней свободы k = r – 1, где r – число интервалов.
Число степеней свободы определяется:
– для однопараметрического распределения по формуле:
k = r – 1, (4.4)
– для многопараметрического распределения по формуле:
k = r – s, (4.5)
где s – число наложенных связей, определяемое по формуле:
s = п + 1 (4.6)
где п – число параметров закона распределения.
Гипотезу о предполагаемом законе распределения считают справедливой при условии  <
<  . Если
. Если  ≥
≥  , гипотезу отвергают.
, гипотезу отвергают.
По таблице 2 приложения 3 с помощью линейной интерполяции определяется значение критической вероятности Ркр. (χ2;k), затем при помощи условия (4.2) делают вывод о принадлежности опытных данных к рассматриваемому закону
Задача 8
С помощью критерия Пирсона определить соответствие данных из примера 2 нормальному закону. В соответствие с задачей 5 принять количество интервалов k =7. Значения параметров задачи 5 сведены в таблицу.
Таблица
| Номер интервала | Границы интервалов | Середина интервала, 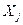
| Число попаданий, 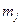
|
| 70 - 107,1 | 88,6 | ||
| 107,1 - 144,3 | 125,7 | ||
| 144,3 - 181,4 | 162,8 | ||
| 181,4 - 218,5 | 200,0 | ||
| 218,5 - 255,6 | 237,1 | ||
| 255,6 - 292,8 | 274,2 | ||
| 292,8 - 329,9 | 311,3 |
Гистограмма распределения случайной величины пробега автомобиля при исправных кулаках тормозной системы при k =7.

Так как площадь гистограммы нормального закона распределения случайной величины равна единице (см.задачу 5), то примем (с некоторым приближением) опытную частоту попадания в седьмом интервал нулю и определим значения функции плотности распределения вероятностей на семи интервалах по теоретическому уравнению:
 , (4,7)
, (4,7)
где S и Δx - параметры распределения; Xj– переменная, в качестве которой принимаем середины интервалов.
Расчеты удобно проводить с помощью таблицы 10.
Расчет значения χ2
Таблица 10
| Номер интервала | Середина интервала
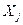
| Теоретическое значение функции плотности распределения вероятности f(xj) | Теоретическая частота mj′ | Опытная частота mj |

|
| 88,6 | 0,00380 | 6,3 | 4,4 | ||
| 125,7 | 0,00260 | 4,3 | 1,2 | ||
| 162,8 | 0,00190 | 3,2 | 0,01 | ||
| 200,0 | 0,00130 | 2,2 | 0,3 | ||
| 237,1 | 0,00079 | 1,32 | 12,5 | ||
| 274,2 | 0,00044 | 0,73 | |||
| 311,3 | 0,00023 | 0,4 | |||
| χ2 = 18,4 |
 0,00380
0,00380
По аналогии определяем: f(x2), f(x3), f(x4), f(x5), f(x6).
Теоретическая частота попаданий mj′ случайной величины в интервал
mj' = n·fj·Δx
m1' = 45·0, 00380·37, 1 = 6, 3
По аналогии определить m2' m3' m4' m5' m6'
У нормального закона распределения два параметра (п = 2-исправное, неисправное), значит число наложенных связей s = п +1 = 3. Так как число интервалов сократилось за счет объединения интервалов, то для многопараметрического распределения по формуле (4.5) число степеней свободы:
k = r – s =5 –3 = 2
На основании анализ опытно-расчётных параметров следует: гипотеза о принадлежности опытных данных к нормальному закону распределения находит подтверждение только на 4-х интервалах, для которых χ2 = 5,91
По полученным значениям k = 2 и χ2 =5,91 методом линейной интерполяции [6] по таблице 2 приложения 3 найти значение.


 В соответствие с критерием Пирсона: Ркр= 0,052 > а = 0,05, где а вероятность неисправного состояния рулевого управления. По таблице 1 приложения 3:
В соответствие с критерием Пирсона: Ркр= 0,052 > а = 0,05, где а вероятность неисправного состояния рулевого управления. По таблице 1 приложения 3:  , следовательно, гипотеза о принадлежности опытных данных нормальному закону не отвергается.
, следовательно, гипотеза о принадлежности опытных данных нормальному закону не отвергается.
|
из
5.00
|
Обсуждение в статье: Проверка с помощью критерия Пирсона |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

