Поведение свободного гироскопа относительно горизонтной системы координат

В качестве примера использования методики составления уравнений движения гироскопических устройств решим вопрос о поведении свободного гироскопа в горизонтной системе координат с помощью формул сферической тригонометрии [6]. Напомним, что свободный гироскоп неподвижен в инерциальном пространстве (относительно звезд), а Земля в этом пространстве вращается. Таким образом, наблюдатель, находящийся в горизонтной (т.е. земной) системе координат, видит движение гироскопа таким же, как и движение звезд.

Для составления уравнений движения свободного гироскопа, установленного в промежуточной широте, в соответствии с изложеной методикой выполним пункты 1-5 (рис.2.3). Система координат горизонтная, так как в дальнейшем речь пойдет о гирокомпасе.

Рис. 2.3.

По п.6 необходимо все угловые скорости, показанные на рис.2.3, спроецировать на связанные с гироскопом оси у и z, т.е. найти = 0 и = 0 в виде

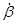= - ω₁ cos(90° - α) = 0 ;

= cos β – ω₂ cos β + ω₁cos α cos (90° - β) = 0.

В соответствии с рис. 2.3 ω₁cos α cos (90° - β) = ω_1z.

Разделим все члены второго уравнения на cos β, получим выражения

= ω₂ - ω₁cos α tg β

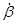= ω₁sin α (2.1)

Данные зависимости (2.1) характеризуют законы движения главной оси свободного гироскопа в азимуте и по высоте относительно горизонтной системы координат.

Анализ этих зависимостей позволяет сделать следующие выводы:

1. В промежуточной широте [ω₁ ≠ 0 и ω₂ ≠ 0) главная ось свободного гироскопа уходит в азимуте относительно плоскости истинного меридиана с угловой скоростью и по высоте относительно плоскости истинного горизонта с угловой скоростью .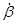

2. Если в начальный момент времени главную ось свободного гироскопа установить в плоскости истинного меридиана (α = 0) и в плоскости истинного горизонта (β = 0), то за счет ω₂ она начнет отклоняться в азимуте с угловой скоростью = ω₂, а за счет появившегося угла α будет двигаться и по высоте с угловой скоростью 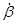= ω₁sin α .

Рассмотренные ситуации подтверждают невозможность использования свободного гироскопа в горизонтной системе координат в качестве курсоуказателя.

В частном случае, если в начальный момент главную ось свободного гироскопа установить таким образом, чтобы α = 0, β = φ, то при этом = 0 и 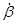= 0. Полученное устройство вырабатывает широту места и называется "гироширотом". Однако практически реализовать приведенные условия с абсолютной точностью невозможно.

С помощью выражений (2.1) можно доказать и первое свойство свободного гироскопа - свойство устойчивости, т.е. сохранения главной осью неизменным заданного ей направления в инерциальном пространстве. Действительно, для инерциальной системы координат следует принять ω₁ = 0 и ω₂ = 0, тогда из (2.1) можно записать:

= 0 ; α = const ;

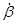= 0 ; β = const .

Из рис.2.3 следует, что при наличии угла α будет иметь место проекция ω₁ на ось у, которая имеет следующее значение:

ω_у = ω₁ cos(90° - α) = ω₁sin α

Проекция ω₁sin α называется полезной составляющей вектора угловой скорости суточного вращения Земли. Она показывает, с какой угловой скоростью около оси у гироскопа вращается в пространстве плоскость истинного горизонта. Следует иметь в виду, что оси гироскопа могут иметь обозначения х, у и z.

Билет № 7