Практическая работа №12 «Вычисление выборочных средней и дисперсии»

Пусть x₁, x₂, …, x_n – данные наблюдений над случайной величиной X. Средним арифметическим наблюдаемых значений случайной величины X называется частное от деления суммы всех этих значений на их число:

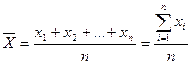(1).

Если данные наблюдений представлены в виде дискретного ряда, где x₁, x₂, …, x_n – наблюдаемые варианты, а m₁, m₂, …, m_n – соответствующие им частоты, причём , то, по определению,

(2).

Вычисленное по данной формуле среднее арифметическое называется взвешенным, так как частоты m_i называются весами, а операция умножения x_i на m_i – взвешиванием.

Для интервального вариационного ряда за x_i принимают середину i-го интервала, а за m_i - соответствующую интервальную частоту:

(3).

Основные свойства среднего арифметического:

1. Среднее арифметическое алгебраической суммы соответствующих друг другу значений равна алгебраической сумме средних арифметических:

.

2. Если ряд наблюдений состоит из двух непересекающихся групп наблюдений, то среднее арифметическое всего ряда наблюдений равно взвешенному среднему арифметическому групповых средних, причём весами являются объёмы соответствующих групп:

.

3. Среднее арифметическое постоянной равно самой постоянной:

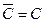
4. Постоянную можно выносить за знак среднего арифметического:

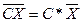
5. Сумма отклонений результатов наблюдений от их среднего арифметического равна нулю:

6. Если все результаты наблюдений увеличить (уменьшить) на одно и то же число, то среднее арифметическое увеличится (уменьшится) на то же число:

7. Если все частоты вариантов умножить на одно и то же число, то среднее арифметическое не изменится.

Выборочной дисперсией значений случайной величины X называется средне арифметическое квадратов отклонений наблюдаемых значений этой величины от их среднего арифметического:

(4).

Если данные наблюдений представлены в виде дискретного ряда, где x₁, x₂, …, x_n – наблюдаемые варианты, а m₁, m₂, …, m_n – соответствующие им частоты, причём , то выборочная дисперсия определяется формулой:

(5).

Используя равенство 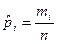, последнюю формулу можно представить в виде:

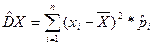(6).

Дисперсия, вычисленная по формулам 5 и 6, называется взвешенной выборочной дисперсией.

Основные свойства выборочной дисперсии:

1. Дисперсия постоянной равна нулю:

2. Если все результаты наблюдений увеличить (уменьшить) на одно и то же число С, то дисперсия не изменится: .

3. Если все результаты наблюдений умножить на одно и то же число С, то имеет место равенство:

.

4. Если все частоты вариантов умножить на одно и то же число, то выборочная дисперсия не изменится.

5. Выборочная дисперсия равна разности между средним арифметическим квадратов наблюдений над случайной величиной X и квадратом её среднего арифметического:

Пример 1.По данным, приведённым в таблице, вычислить среднее арифметическое и дисперсию числа неправильных соединений в минуту.

 

Индекс	i
Число неправильных соединений в минуту	xi
Частота	mi
частость		8/60	17/60	16/60	10/60	6/60	2/60	1/60

 

Решение.Среднее арифметическое вычислим по формуле 2:

Дисперсию вычисляем по формуле 5:

Пример 2.По данным, приведённым в таблице, вычислить среднее арифметическое и дисперсию диаметра валика.

Решение.Среднее арифметическое вычислим по формуле 3:

Дисперсию вычисляем по формуле 6: