Объемное напряженное состояние

Объемным или трехосным называется напряженное состояние, при котором все три главных напряжения отличны от нуля (рис.3.4).

Рассмотрим вопрос определения касательных напряжений в площадках, проходящих через одну из координатных осей x, y или z (рис.3.1).

Используя принцип независимости действия сил и результаты решения прямой задачи для линейного и плоского напряженных состояний, получим:

; ;

;

При a = 45⁰, касательные напряжения достигают наибольших значений:

; ; ,

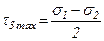c учетом того, что , получим:

Таким образом, площадка с наибольшим касательным напряжением наклонена под углом α=45⁰ к главным площадкам с напряжениями .

Также можно доказать, что

.

.

1. Главные напряжения при плоском изгибе.

Ответ:

Площадки, по которым не действуют касательные напряжения, называются главными площадками, а нормальные напряжения на этих площадках — главными напряжениями.

Главные напряжения обозначают: s₁, s₂, s₃ и s₁> s₂> s₃

 

Главные напряжения при поперечном изгибе:

.

 

Главные напряжения в наиболее опасных точках (А и В):

 

Билет №21.

 

1. Эпюры внутренних силовых факторов.

Ответ:

 

 

1. Понятие о деформированном состоянии в точке. Компоненты деформации и их обозначения. Главные оси деформации.

Ответ:

Деформированное состояние в точке– это совокупность относительных линейных деформаций и углов сдвига для всевозможных направлений осей, проведенных через данную точку.

При этом можно сделать утверждение, что деформированное состояние в точке вполне определено, если задан тензор деформаций для этой точки.

Компоненты тензора деформаций при повороте осей изменяются совершенно аналогично компонентам тензора напряжений (по законам тензорного преобразования). Так, при плоском напряженном состоянии деформации в некоторой плоскости на произвольной наклонной площадке можно выразить через главные деформации и угол наклона α следующим образом:

221212cossin;1sin2.22ααε=ε⋅α+ε⋅αε−ε⋅γ=⋅α

Главные деформации можно выразить через произвольные деформации по двум взаимно перпендикулярным площадкам в виде:

 

а положение главных площадок будет задаваться углом α, который определяется из выражения:

1. Анализ напряжённого состояния в поперечном сечении балки.

Ответ:

Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по всем площадкам (сечениям), содержащим данную точку.

Исследование напряженного состояния дает возможность анализировать прочность материала для любого случая нагружения тела.

Пусть в окрестности исследуемой точки шестью попарно параллельными плоскостями выделен элементарный прямоугольный параллелепипед с размерами ребер dx, dy и dz (рис.3.1). По его граням будут действовать нормальные “s_i” и касательные “t_ij” напряжения.

Обозначения нормальных напряжений содержат один индекс - наименование оси, которой параллельно данное напряжение. В обозначении касательных напряжений используются два индекса: первый совпадает с индексом нормального напряжения, действующего по данной площадке, а второй - наименование оси, которой параллельно данное касательное напряжение.

Используем принятое правило знаков для напряжений. Нормальное напряжение σ считается положительным, если совпадает по направлению с внешней нормалью к площадке, касательные напряжения t считаются положительными, если вектор касательных напряжений следует поворачивать против хода часовой стрелки до совпадения с внешней нормалью (рис.3.2). Отрицательными считаются напряжения обратных направлений (рис.3.3).

 

 

Билет №22.

 

1. Деформированное состояние при растяжении (сжатии). Коэффициент Пуассона.

Ответ:

При растяжении стержня его длина увеличивается, а размеры поперечного сечения уменьшаются, при сжатии наоборот.

Изменение длины стержня 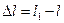называют линейной продольной деформацией (абсолютным удлинением); изменение размеров поперечного сечения 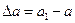- линейной поперечной деформацией.

Интенсивность деформирования оценивают деформациями, приходящимися на единицу длины (размер сечения) стержня: относительной продольной 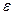и относительной поперечной : .

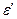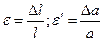Относительные деформации часто определяют в процентах. При растяжении продольную деформацию (удлинение) считают положительной, поперечную (сужение сечения) – отрицательной. Экспериментально установлено, что между относительными поперечной и продольной деформациями существует зависимость

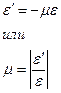
Здесь - коэффициент поперечной деформации, или коэффициент Пуассона.

1. Общая линейная зависимость между компонентами напряжённого и деформированного состояний.

Ответ:

Касательные напряжения вызывают угловые деформации, причем при малых деформациях они не влияют на изменение линейных размеров, и следовательно, на линейные деформации. Поэтому они справедливы также в случае произвольного напряженного состояния и выражают так называемый обобщенный закон Гука.

Угловая деформация gxy обусловлена касательным напряжением txy, а деформации gxz и gyz - соответственно напряжениями txz и tyz. Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости

которые выражают закон Гука при сдвиге. Коэффициент пропорциональности G называется модулем сдвига. Существенно, что нормальное напряжение не влияет на угловые деформации, так как при этом изменяются только линейные размеры отрезков, а не углы между ними.

 

1. Траектории главных напряжений.

Ответ:

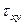Рассмотрим две взаимно-перпендикулярные площадки с касательными напряжениями и 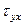. Согласно закону парности касательных напряжений знак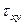и и 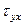противоположны. Поэтому, если площадку с напряжением 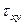поворачивать до совпадения с площадкой с напряжением 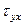, то обязательно найдется такое положение площадки, когда .

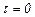Площадки, по которым касательные напряжения равны нулю, называются главными, а действующие по этим площадкам нормальные напряжения - главными напряжениями.

Главные напряжения обозначаются 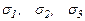, причем 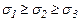. Элемент, выделенный главными площадками, изображен на рис.3.5. В зависимости от количества действующих главных напряжений различают три вида напряженных состояний: линейное, плоское и объемное.

 

 

Билет №23.

 

 

1. Закон Гука при растяжении (сжатии). Модуль упругости первого рода.

Ответ:

Oпыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии - наоборот (рис.1).

Абсолютная продольная и поперечная деформации равны

; .

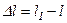Относительная продольная деформация e и относительная поперечная деформация e' равны

; .

В пределах малых удлинений для большинства материалов справедлив закон Гука - нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформацииe

.

Коэффициент пропорциональности E - модуль продольной упругости, его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки.

 

1. Удельная потенциальная энергия деформации. Энергия изменения формы и изменения объёма.

Ответ:

Удельной потенциальной энергией деформации u называется величина потенциальной энергии деформации U, накопленной в единице объема тела V. Для линейного напряженного состояния:

.

Используя принцип независимости действия сил, полученный результат можно обобщить на случай объемного напряженного состояния:

.

В случае площадок общего положения (не главных площадок) выражение для удельной потенциальной энергии приобретает вид:

.

Предыдущее выражение можно преобразовать с помощью формул обобщенного закона Гука к виду:

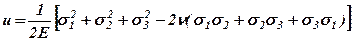. (3.5)

Рассмотрим напряженное состояние чистого сдвига. Запишем выражение удельной потенциальной энергии деформации по площадкам чистого сдвига:

.

С другой стороны чистый сдвиг - это двухосное напряженное состояние с главными напряжениями ; , поэтому можно записать u как

.

Очевидно, величина удельной потенциальной энергии деформации u не должна зависеть от того по каким площадкам она записана, поэтому , откуда, как упоминалось ранее .

Таким образом, постоянные упругости материалов, характеризующие жесткость при растяжении и сдвиге и поперечную деформацию, являются зависимыми. Поэтому достаточно определить лабораторным путем при растяжении две характеристики упругости Е и n, а третья G может быть вычислена аналитически.

 

1. Потенциальная энергия упругой деформации.

Ответ:

Элементарная работа статически приложенного внешнего момента Т на перемещении равна:

.

При чистом кручении М_к = Т и .

Потенциальная энергия деформации

;

интегрируя выражение для элементарной работы по всей длине l стержня, получим

.

При М_к = const и = const, получим

.

Билет №24.

 

1. Определение осевых перемещений поперечных сечений. Эпюры перемещений.

Ответ:

???????????????????????????????????????????????????????????????????????????????????????

1. Объёмная деформация и закон Гука.

Ответ:

Обобщенный закон Гука (закон Гука при объемном напряжении):

e₁,e₂,e₃ — относительные удлинения в главных направлениях (главные удлинения). Если какие-либо из напряжений s_i будут сжимающими, то их необходимо подставлять в формулы со знаком минус.

Относительная объемная деформация:

 

Изменение объема не зависит от соотношения между главными напряжениями, а зависит от суммы главных напряжений. Т.е. элементарный кубик получит такое же изменение объема, если к его граням будут приложены одинаковые средние напряжения: , тогда , где К= — модуль объемной деформации. При деформации тела, материал которого имеет коэффициент Пуассона m= 0,5 (например, резина) объем тела не меняется.

 

1. Упруго-пластичный изгиб балки.

Ответ:

???????????????????????????????????????????????????????????????????????????????????????

 

 

Билет №25.

 

1. Энергия деформации при растяжении.

Ответ:

При растяжении стержня внешняя сила совершает работу вследствие перемещения точки ее приложения (рис.2.8). При статическом приложении внешней силы ее величина возрастает прямо пропорционально деформации . Элементарная работа статической силы Р на перемещении равна

.

Работа на перемещении Δl равна

.

Подставляя сюда соотношение , получим . Выражая Δl из закона Гука, окончательно получим формулу для работы внешней силы, совершаемой на перемещении точки ее приложения

.

В сечении, бесконечно близком к точке приложения силы Р, действует продольная сила N, которая также как и сила Р прикладывается статически. Она также совершает работу .

Вследствие закона сохранения энергии работа продольной силы N равна потенциальной энергии деформации U и равна.

.

Единицей измерения потенциальной энергии деформации является 1H×м = 1Дж.

 

1. Плоское напряжённое состояние, его особенности и частные случаи.

Ответ: