 |
Главная |
Частные случаи плоского напряженного состояния
|
из
5.00
|
Билет №1.
- Сопротивление материалов как часть механики деформированного тела. Связь сопротивления материалов с другими областями знаний.
Ответ:
Все современные конструкции, машины, приборы и сооружения изготавливают или строят по заранее разработанным проектам. Проект - это чертеж или ряд чертежей и технических рисунков, в которых указываются все размеры элементов конструкций и деталей машин, необходимых для изготовления, их материалы, а также приводится описание технологии. Таким образом, еще в процессе проектирования необходимо уметь определять размеры элементов и деталей, входящих в состав сооружений или машин. Вполне очевидно, что эти размеры зависят от ряда условий и обстоятельств, в том числе от свойств материала изделия и от предполагаемых на него внешних воздействий.
Любая конструкция должна обладать надежностью при эксплуатации и быть экономичной.
Надежность конструкции обеспечивается, если она сохраняет прочность, жесткость и устойчивость при гарантированной долговечности. Ее экономичность в значительной мере определяется расходом материала, применением менее дефицитных конструкционных материалов, возможностью изготовления деталей по наиболее прогрессивным технологиям. Надежность и экономичность - противоречивые требования.
В сопротивлении материалов широко применяются методы теоретической механики и математического анализа, используются данные из разделов физики, изучающих свойства различных материалов, материаловедения и других наук.
Сопротивление материалов является наукой экспериментально-теоретической, так как она широко использует опытные данные и теоретические исследования.
Таким образом, основная задача сопротивления материалов состоит в разработке инженерных методов конструирования и расчета наиболее типичных элементов конструкций на прочность, жесткость и устойчивость при заданной долговечности, одновременно обеспечивающих экономичность.
- Определение осевых перемещений поперечных сечений. Эпюры перемещений.
Ответ:
В результате растяжения (сжатия) сечения стержня перемещаются. Осевое перемещение 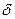 одного сечения относительно другого равно изменению длины участка стержня между этими сечениями. График, показывающий перемещения всех сечений стержня относительно неподвижного (или условно принятого за неподвижное), называют эпюрой перемещений.
одного сечения относительно другого равно изменению длины участка стержня между этими сечениями. График, показывающий перемещения всех сечений стержня относительно неподвижного (или условно принятого за неподвижное), называют эпюрой перемещений.
- Плоское напряжённое состояние. Его особенности и частные случаи.
Ответ:
Плоское напряженное состояние
Плоским или двухосным называется напряженное состояние, при котором одно из трех главных напряжений равно нулю.
Частные случаи плоского напряженного состояния
Всестороннее растяжение
Напряженное состояние, при котором главные напряжения, действующие по граням параллелепипеда равны между собой  =
=  = s, называется всесторонним растяжением. В этом случае, получим
= s, называется всесторонним растяжением. В этом случае, получим
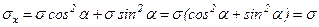 ,
, 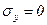 ,
,
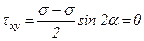 ,
, 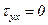 ,
,
то есть, нормальные напряжения в любой произвольной площадке равны между собой  =
=  =
= 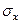 =
= 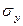 = s, а касательные напряжения равны нулю:
= s, а касательные напряжения равны нулю: 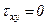 ,
, 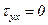 .
.
Чистый сдвиг
Пусть по граням параллелепипеда действуют главные напряжения  =s,
=s,  = - s , (рис.3.10).
= - s , (рис.3.10).
Определим величины нормальных и касательных напряжений, действующих в площадках повернутых под углом 45о к главным. Из формул (3.1) получим, что
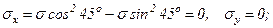

Напряженное состояние, при котором по граням выделенного элемента действуют только касательные напряжения, называется чистым сдвигом, а площадки - площадками чистого сдвига.
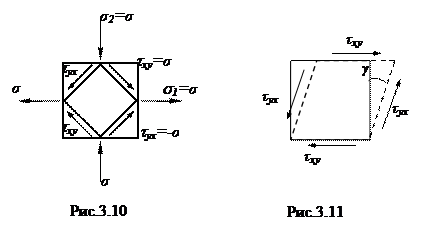
Экспериментально установлено, что существует линейная зависимость между углом сдвига g и касательными напряжениями t (рис.3.11), являющейся законом Гука при сдвиге
 ,
,
где G – модуль сдвига, характеризующий способность материала сопротивляться сдвиговой деформации, т.е. характеризующая жесткость материала при сдвиге.
Величина модуля сдвига связана с модулем упругости при растяжении Е и коэффициентом Пуассона ν соотношением
 |
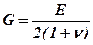 .
.
Билет №2.
- Классификация объектов изучения.
Ответ:
В сопротивлении материалов рассматриваются вопросы расчёта на прочность, жёсткость и устойчивость элементов инженерных конструкций и деталей машин.
Прочность – свойство материалов воспринимать в определённых пределах, не разрушаясь, приложенные к ним нагрузки.
Жёсткость – это способность тела или конструкции сопротивляться деформации.
Деформацией называется изменение взаимного расположения точек тела под действием внешних воздействий.
Если после снятия внешнего силового воздействия, точки тела возвращаются в своё первоначальное положение, то такая деформация называется упругой. В противном случае деформация, оставшаяся после разгрузки называется остаточной или пластической.
Устойчивость – способность системы сохранять первоначальную форму равновесия под воздействием внешней нагрузки. При потере устойчивости система обычно внезапно переходит к новой форме равновесия.
- Жёсткость и податливость при растяжении (сжатии). Энергия деформации при растяжении.
Ответ:
Жёсткость – это способность тела или конструкции сопротивляться деформации.
При растяжении стержня его длина увеличивается, а размеры поперечного сечения уменьшаются, при сжатии наоборот.
Относительные деформации часто определяют в процентах. При растяжении продольную деформацию (удлинение) считают положительной, поперечную (сужение сечения) – отрицательной. Экспериментально установлено, что между относительными поперечной и продольной деформациями существует зависимость
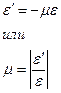
Выражение полной потенциальной энергии, накопленной стержнем:
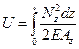
Потенциальную энергию, накапливаемую в единице объёма, называют удельной потенциальной энергией деформации:
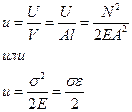
Единицей энергии в СИ является джоуль (Дж), а объёма - 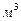 , следовательно, единица удельной потенциальной энергии деформации -
, следовательно, единица удельной потенциальной энергии деформации - 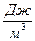
- Напряжения на наклонной площадке. Определение положения главных площадок и значений главных напряжений.
Ответ:
Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по всем площадкам (сечениям), содержащим данную точку.
Касательные напряжения по двум взаимно перпендикулярным площадкам равны по величине и противоположны по знаку:
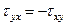 ,
, 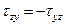 ,
, 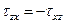 .
.
Рассмотрим две взаимно-перпендикулярные площадки с касательными напряжениями 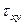 и
и 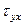 . Согласно закону парности касательных напряжений знаки
. Согласно закону парности касательных напряжений знаки 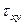 и
и 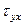 противоположны. Поэтому, если площадку с напряжением
противоположны. Поэтому, если площадку с напряжением 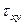 поворачивать до совпадения с площадкой с напряжением
поворачивать до совпадения с площадкой с напряжением 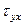 , то обязательно найдется такое положение площадки, когда
, то обязательно найдется такое положение площадки, когда 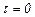 .
.
Площадки, по которым касательные напряжения равны нулю, называются главными, а действующие по этим площадкам нормальные напряжения - главными напряжениями.
Главные напряжения обозначаются 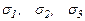 , причем
, причем 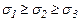 . Элемент, выделенный главными площадками, изображен на рис.3.5. В зависимости от количества действующих главных напряжений различают три вида напряженных состояний: линейное, плоское и объемное.
. Элемент, выделенный главными площадками, изображен на рис.3.5. В зависимости от количества действующих главных напряжений различают три вида напряженных состояний: линейное, плоское и объемное.
Билет №3.
- Основные понятия и гипотезы.
Ответ:
Гипотеза плоских сечений (гипотеза Бернулли) – сечения стержня, плоские и перпендикулярные к его оси до деформации, остаются плоскими и перпендикулярными к оси и после деформации.
Растяжением или сжатием называют такой вид деформации бруса (стержня), при котором в его поперечных сечениях возникает только продольная сила N.
Равенство по абсолютному значению и противоположность по направлению касательных напряжений, действующих на взаимно перпендикулярных площадках, называют законом парности касательных напряжений.
Изменение длины стержня 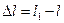 называют линейной продольной деформацией (абсолютным удлинением); изменение размеров поперечного сечения
называют линейной продольной деформацией (абсолютным удлинением); изменение размеров поперечного сечения 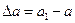 - линейной поперечной деформацией.
- линейной поперечной деформацией.
Интенсивность деформирования оценивают деформациями, приходящимися на единицу длины (размер сечения) стержня: относительной продольной 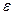 и относительной поперечной
и относительной поперечной 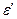 :
: 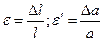 .
.
- Экспериментальное изучение механических свойств материалов при растяжении (сжатии). Истинные и условные диаграммы растяжения материалов в пластическом состоянии. Предел пропорциональности, упругости, текучести, прочности.
Ответ:
При выборе материала для проектируемого элемента конструкции, для расчёта его на прочность и жёсткость необходимо знать механические свойства материалов, к основным из которых относятся: прочность, пластичность, упругость, твёрдость.
Прочность – способность материала сопротивляться разрушению при действии внешних нагрузок.
Пластичность – способность материала накапливать до разрушения остаточные (пластические) деформации.
Упругость – способность материала восстанавливать первоначальные размеры и форму детали после снятия внешних нагрузок.
Твёрдость – способность материала оказывать сопротивление деформированию и разрушению при местных контактных воздействиях.
Для определения опасных напряжений s0 необходимо провести испытания образцов материала на растяжение и сжатие.
При испытании разные материалы обнаруживают различное поведение при нагружении, в соответствии, с чем все материалы делятся на две большие группы: пластичные и хрупкие.
Диаграммы пластичного материала Ст.3, полученные при испытании на растяжение и сжатие приведены на рис.2.5, диаграммы хрупкого материала СЧ-12-28 – на рис.2.6.
Пластичные материалы на диаграмме растяжения часто имеют характерный участок, называемый площадкой текучести, ему соответствуют напряжения - предел текучести σт. Явление текучести сопровождается образованием больших пластических, остаточных деформаций. Появление таких деформаций в элементах конструкции, как правило, приводит к нарушениям в работе конструкции, и являются нежелательными.
К весьма пластичным материалам относятся медь, алюминий, латунь, малоуглеродистая сталь и др. Менее пластичными являются дюраль и бронза. Мерой пластичности является относительное остаточное удлинение при разрыве d. Чем больше d, тем более пластичным считается материал.

Хрупкие материалы выдерживают напряжения равные пределу прочности σв и разрушаются без образования заметных остаточных деформаций. К хрупким материалам относятся чугун, высокоуглеродистая инструментальная сталь, стекло, кирпич, строительные камни и др. Для таких материалов величина удлинения при разрыве d не превышает 2¸5%, а в ряде случаев измеряется долями процента.
Для пластичных материалов за предельные (опасные) напряжения s0, для того чтобы избежать в работающей конструкции образование заметных остаточных деформаций, обычно принимают предел текучести sт.
Для хрупких, а в некоторых случаях и умеренно пластичных материалов, за s0 принимается предел прочности sв.
Сопоставление предела прочности хрупких материалов при растяжении sв р с пределом прочности при сжатии sв с показывает, что эти материалы обладают, как правило, более высокими прочностными показателями при сжатии, нежели при растяжении. Величина отношения 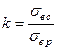 для чугуна колеблется в пределах 2,5…5, а для керамических материалов k = 5…10.
для чугуна колеблется в пределах 2,5…5, а для керамических материалов k = 5…10.
- Круги напряжений (круги Мора).
Ответ:
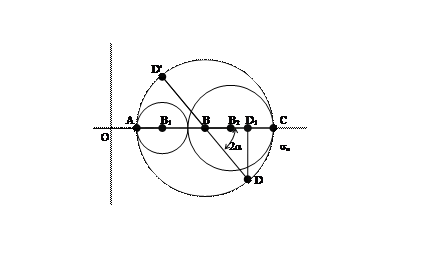
Выражения
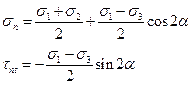
задают в параметрическом виде уравнение окружности в координатах 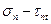 (ось
(ось 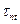 направлена вниз). Отрезки ОС, ОА и ОВ в соответствующем масштабе представляют нам
направлена вниз). Отрезки ОС, ОА и ОВ в соответствующем масштабе представляют нам 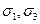 и
и 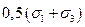 соответственно. Точка В – центр окружности. Тогда отрезок
соответственно. Точка В – центр окружности. Тогда отрезок 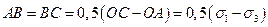 - радиус окружности (R). Отсчитывая угол
- радиус окружности (R). Отсчитывая угол 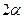 от точки С по часовой стрелке (отрицательный угол), мы находим точку D, координаты которой (отрезки DD1 и OD1) соответствует напряжениям
от точки С по часовой стрелке (отрицательный угол), мы находим точку D, координаты которой (отрезки DD1 и OD1) соответствует напряжениям 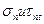 в площадке, нормаль к которой направлена под отрицательным углом
в площадке, нормаль к которой направлена под отрицательным углом  к направлению
к направлению 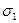 . Действительно
. Действительно
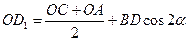 или
или 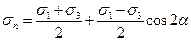 ; или, учитывая, что синус отрицательного угла отрицателен, имеем:
; или, учитывая, что синус отрицательного угла отрицателен, имеем:
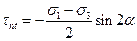 .
.
Таким образом, координаты точек окружности радиусом 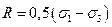 представляют семейства нормальных
представляют семейства нормальных 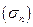 и касательных
и касательных 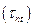 напряжений, действующих в площадках, параллельных напряжению
напряжений, действующих в площадках, параллельных напряжению  . Аналогично можно построить окружности, точки которых будут представлять напряжения в семействе площадок, параллельных напряжению
. Аналогично можно построить окружности, точки которых будут представлять напряжения в семействе площадок, параллельных напряжению 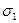 (центр окружности в точке
(центр окружности в точке 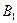 ) и напряжению
) и напряжению 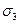 (центр окружности в точке
(центр окружности в точке 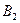 ). Эти окружности называются круговыми диаграммами напряжённого состояния (круги Мора).
). Эти окружности называются круговыми диаграммами напряжённого состояния (круги Мора).
Билет №4.
- Геометрические характеристики плоских сечений. Моменты плоских сечений.
Ответ:
При растяжении и сжатии площадь поперечного сечения полностью характеризует прочность и жесткость стержня. Возьмем некоторое поперечное сечение бруса (рис. 1). Если представить себе сечение состоящим из бесчисленного множества площадок dF, то площадь всего сечения 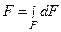 . Площадь является простейшей геометрической характеристикой сечения, имеет размерность L2. Отметим два важных свойства: площадь всегда положительна и не зависит от выбора системы координат.
. Площадь является простейшей геометрической характеристикой сечения, имеет размерность L2. Отметим два важных свойства: площадь всегда положительна и не зависит от выбора системы координат.
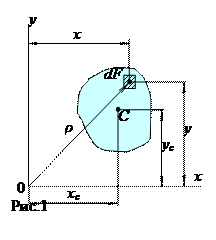 При расчетах на изгиб, кручение, сложное сопротивление и устойчивость используются более сложные геометрические характеристики: статические моменты, моменты инерции сечений, которые зависят не только от формы и размеров сечений, но также от положения осей и точек (полюсов), относительно которых они вычисляются.
При расчетах на изгиб, кручение, сложное сопротивление и устойчивость используются более сложные геометрические характеристики: статические моменты, моменты инерции сечений, которые зависят не только от формы и размеров сечений, но также от положения осей и точек (полюсов), относительно которых они вычисляются.
Статическим моментом Sx сечения относительно оси х называется геометрическая характеристика, определяемая интегралом вида
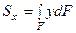 , (1)
, (1)
где у - расстояние от элементарной площадки dF до оси х.
|
из
5.00
|
Обсуждение в статье: Частные случаи плоского напряженного состояния |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

