 |
Главная |
Матрицы, виды матриц, линейные операции над матрицами. Произведение матриц
|
из
5.00
|
Матрица – это таблица из m строк и n столбцов.
Если все элементы матрицы Am×n равны нулю, то такая матрица называется нулевой и обозначается обычно буквой O.
Матрица размера 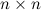 называется квадратной, число
называется квадратной, число  называется порядком матрицы.
называется порядком матрицы.
Верхней треугольной матрицей называется матрица, все элементы которой ниже главной диагонали равны нулю.
Пример верхней треугольной матрицы. 
Ступенчатой матрицей называется матрица, удовлетворяющая следующим условиям:
если матрица содержит нулевую строку, то все строки, расположенные под нею, также нулевые;
если первый ненулевой элемент некоторой строки расположен в столбце с номером i, и следующая строка не нулевая, то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем i.

Произведение матрицы на число

Сумма матриц

Произведение матриц

Транспонирование
Транспонирование матрицы - это операция над матрицей, когда ее строки становятся столбцами с теми же номерами.

Элементарные преобразования матриц. Обратная матрица.
Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц, то есть, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Элементарными преобразованиями строк называют:
-перестановку местами любых двух строк матрицы;
-умножение на ненулевую константу любой строки матрицы;
-прибавление к любой строке матрицы другой строки, умноженной на ненулевое число.
Матрицы A и B называют эквивалентными матрицами если от матрицы A к матрице B перешли с помощью элементарных преобразований над строками и обозначают A ~ B.
Обратная матрица.
1) Вычислить, что она квадратная.
2) Вычислить определитель квадратной матрицы (если d=0, то прекращаем). 
3) Транспонируем (строки и столбцы меняем местами)
4) Присоединенную матрицу найти (каждый элемент транспонированной матрицы заменяем его алгебраическим дополнением )  Алгебраическим дополнением элемента
Алгебраическим дополнением элемента  матрицы
матрицы 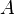 называется число
называется число 
5. 
Геометрический вектор, линейные операции над векторами.
1. Сложение векторов. 

2. Вычитание векторов.  .
.

3. Умножение вектора на число.

Свойства линейных операций:
1)  ;
;
2)  ;
;
3)  ;
;  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7)  ;
;  ;
;
Скалярное произведение векторов, его свойства, вычисление. Векторное произведение векторов и его свойства.
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:
a · b = |a| · |b| cos α
|
из
5.00
|
Обсуждение в статье: Матрицы, виды матриц, линейные операции над матрицами. Произведение матриц |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

