 |
Главная |
Вторая теорема Больцано – Коши
|
из
5.00
|
Пусть функция f (x) определена и непрерывна на отрезке [a, b]. Если на концах этого отрезка функция принимает неравные значения f(a) = A, f (b) = B, то, каково бы ни было число m  (A, B), найдётся такая точка х = с
(A, B), найдётся такая точка х = с  (a, b), что f (c) = m (.
(a, b), что f (c) = m (.
Как частный случай имеет место следующее утверждение. Пусть функция f(x) непрерывна на отрезке [a, b] и на концах отрезка имеет значения разных знаков. Тогда существует внутренняя точка отрезка с  (a, b), в которой f(c) = 0.
(a, b), в которой f(c) = 0.
Данная теорема имеет простой геометрический смысл: непрерывная кривая при переходе из одной полуплоскости, граница которой является ось абсцисс, в другую, пересекает эту ось .
Теорема. Если функция f (x) определена и непрерывна на отрезке [a, b] , то она на этом отрезке принимает по крайней мере один раз любое значение, заключённое между её наименьшими и наибольшими значениями.
Д о к а з а т е л ь с т в о. Будем считать, что А < m < B. Рассмотрим на промежутке [а, b] вспомогательную функцию φ (x) = f (x) − m. Эта функция непрерывна на промежутке [а, b] и на концах его имеет разные знаки: φ (a) = f (a) − m = A − m < 0 и φ(b) = f(b) − m = B − m > 0. Тогда, по второй теореме Больцано – Коши, между a и bнайдётся точка х = с, для которой φ(c) = m. Что и требовалось доказать.
44 вопрос
Обратная функция и её непрерывность.
Пусть функция y=f(x), заданная на множестве X, обратима. Это значит, что функция f различным значениям аргумента ставит в соответствие различные значения функции, т.е. для любых x1,x2∈X : x1/=x2⇒f(x1)/=f(x2).
В этом случае для каждого y∈Y=f(X) существует один и только один элемент x∈X такой, что y=f(x). А это означает, что на множестве Y определена функция g:Y→X , которую и называют обратной функцией к функции y=f(x) и обозначают: x=f−1(y). При этом очевидно, что функция f являетсяобратной к функции f−1. Поэтому функции y=f(x) и x=f−1(y) называют взаимно обратными.
Т.о., если функция f:X→Y , где Y=f(X), обратима, то для нее существует единственная обратная функция f−1:Y→X и если y=f(x) то x=f−1(y), и если x=f−1(y), то y=f(x) и f−1(f(x))=x при любом x∈X , f−1(f(y))=y при любом
y∈Y .
График. Переход от функции y=f(x), x∈X , к обратной функции x=f−1(y), y∈Y (если она существует), сводится лишь к измерению ролей множеств X и Y. Поэтому графики функций y=f(x) и x=f−1(y) на плоскости XOY совпадают. Но обычно и для обратной функции аргумент обозначают через y, т.е. записывают ее в видеy=f−1(x), x∈Y . Тогда график функции y=f−1(x) получается из графика прямой функции y=f(x) с помощью преобразования плоскости XOY, переводящей каждую точку (x,y) в точку(y,x), т.е. симметрией относительно прямой y=x.
Обычно, говоря об обратной функции, заменяют x на y, а y на x (x↔y ) и пишут y=f−1(x). Очевидно, что исходная функция f(x)и обратная функция f−1(x) удовлетворяют соотношению: f−1(f(x))=f(f−1(x))=x.
Графики исходной и обратной функции получаются друг из друга зеркальным отображением относительно биссектрисы первого квадранта.
Монотонные функции и их свойства.
Пусть функция f(x)определена в некоторой области X. Функция называется возрастающей (убывающей) в этой области, если для любой пары принадлежащих ей значений x1и x2 из x1>x2следуетf(x1)>f(x2) (f(x1)<f(x2)). Если же из x1>x2 следует f(x1)≥f(x2) (f(x1)≤f(x2)) , то функцию называют неубывающей (невозрастающей).
Иногда удобнее и в этом случае называть функцию возрастающей (убывающей) - но в широком смысле.
Функции всех этих типов носят общее название монотонных.
Существование и непрерывность обратной функции.
Теорема 1. Если функция y=f(x) строго возрастает (убывает) на множестве X, то для нее существуетобратная функция x=f−1(y), которая определена на множестве Y=f(X) и является на Y строго возрастающей (убывающей).
Доказательство. По условию функция f строго возрастает на множестве X. Это значит для любых x1,x2∈X и x1<x2 следует f(x1)<f(x2). Отсюда следует, что функция f обратима на X, следовательно, для нее существует обратная функция f−1:Y→X . Покажем, что функция f−1 строго возрастает на множестве Y. Пусть y1 и y2- любые точки из Y и y1<y2. Докажем, что x1=f−1(y1)<x2=f−1(y2). Допустим, чтоx1≥x2 . По условию функция f строго возрастает на X, поэтому из условия x1≥x2 вытекает неравенствоy1=f(x1)≥y2=f(x2) , что противоречит условию y1<y2.
Т.о., условие строгой монотонности функции является достаточным для существования обратной функции.
Теорема 2. Если функция y=f(x) строго возрастает (убывает) и непрерывна на промежутке I, то существует обратная функция x=f−1(y), которая определена на промежутке Ef=f(I) и является на Е, строго возрастающей (убывающей) и непрерывной.
Доказательство. Для определенности предположим, что функция f строго возрастает на промежутке I. По следствию из 2-ой теоремы Больцано-Коши область значений Ef=f(I) непрерывной функции f тоже есть промежуток. В силу строгого возрастания функции f для каждого y∈E существует единственная точка x∈I такая, что f(x)=y. Следовательно для функции f существует обратная функция f−1определенная на промежутке Е и с множеством значений I.
Покажем, что f−1 строго возрастает на Е. Пусть y1 и y2-- две произвольные точки из Е, такие, что y1<y2 и прообразами этих точек будут точки x1и x2. f−1(y1)=x1, и f−1(y2)=x2.
Поскольку f - строго возрастающая функция, то неравенство y1=f(x1)<f(x2)=y2 возможно тогда и только тогда когда x1<x2 или тоже самое, когда f−1(y1)<f−1(y2). В силу произвольности y1 и y2 ∈E делаем вывод, что функция f−1 - строго возрастает на множестве Е. Что и требовалось доказать.
45. Производная функции, её геометрический и физический смысл.
Производной функции 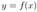 в точке
в точке  называется предел отношения приращения функции в этой точке к приращению аргумента
называется предел отношения приращения функции в этой точке к приращению аргумента  . при
. при  (если этот предел существует и конечен), т.е.
(если этот предел существует и конечен), т.е.
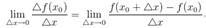
Обозначают: 
Производной функции  в точке
в точке 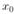 справа (слева) называется
справа (слева) называется 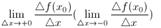 (если этот предел существует и конечен).
(если этот предел существует и конечен).
Обозначают:  – производная y=f(x) в точке
– производная y=f(x) в точке  справа,
справа, 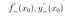 – производная y=f(x) в точке
– производная y=f(x) в точке  слева.
слева.
|
из
5.00
|
Обсуждение в статье: Вторая теорема Больцано – Коши |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

