Замечательные пределы

Число А называется пределом функции у=f(x) при х àx₀, если для любой последовательности хn сходящейся к знамению х₀ соответствующей послед. f(x_n) сходится к числу А.

Первый замечательный предел: при хà0 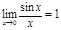При вычислении приделов с неопределённостью «0/0»и содержащий тригонометрические функции используют первый замечательный предел.

Второй замечательный предел: где n Если х ,то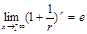

Вопрос 43

Определение непрерывности функции

Пусть функция f (x) определена в некоторой окрестности точки х₀. Функция f (x) называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т. е.

(5.1)

Или ( ε > 0 ) ( δ = δ (ε, x₀) > 0 ) ( | x - x₀ | < δ ) : | f ( x ) − f ( x₀) | < ε

Для непрерывности функции в точке требуется выполнение двух условий: существование предела функции в данной точке и совпадение этого предела с тем значением, которое функция принимает в этой точке. Так как , то соотношение (5.1) можно записать в следующем виде:

т. е. для непрерывной функции можно переставить знак функции и знак предела. Если функция непрерывна в точке х₀, то она определенна в этой точке, т.е. существует f(x₀). Если

то функция непрерывна в этой точке. Это определение вытекает из свойства предельного перехода функции в данной точке.
Перенесем в равенстве (5.1) f (x₀) под знак предела. Так как условие х → х₀ и (х − х₀) → 0 равносильны, то получаем

(5.2)

Разность Δx = x - x₀ называется приращением аргумента х в точке x₀, разность Δy = f (x) − f (x₀) называется приращением функции в точке х₀, вызванным приращением аргумента Δх

При фиксированной точке х₀ величина Δу является функцией аргумента Δ х. Равенство (5.2) в новых обозначениях принимает вид

(5.3)

(5.3) является свойством непрерывной функции, которое можно сформулировать так: функция f (x) является непрерывной в точке х₀, если ее приращение в этой точке является бесконечно малой функцией при Δх → 0.

Непрерывность функций на интервале

Будем говорить, что функция f (x) непрерывна в интервале (а, b), если она непрерывна в каждой точке этого интервала; непрерывна на отрезке [а, b], если она непрерывна в интервале (а, b) и непрерывна в точке x = а справа, а в точке x = b слева, т. е.

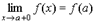и

Кусочно-непрерывные функции

Функция f (x) называется кусочно-непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках [а, b] за исключением, быть может, конечного числа точек, в которых имеет разрыв первого рода и, кроме того, имеет односторонние пределы в точках a и b
Функция называется кусочно-непрерывной на числовой прямой, если она кусочно - непрерывна на любом отрезке числовой прямой.