 |
Главная |
Пример выполнения заданий практической части
|
из
5.00
|
Пример 1. Даны матрицы 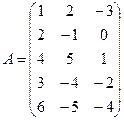 ;
; 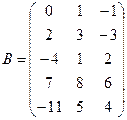 ;
; 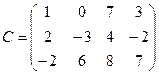 . Найти сумму А+В и произведение А´С.
. Найти сумму А+В и произведение А´С.
Решение.
 .
.
Пусть А´С=D. Тогда
d11=1×1+2×2+(-3) ×(-2)=11
d12=1×0+2×(-3)+(-3) ×6=-24
d13=1×7+2×4+(-3) ×8=-9
d14=1×3+2×(-2)+(-3) ×7=-22
d21=2×1+(-1) ×2+0×(-2)=0
d22=2×0+(-1) ×(-3)+0×6=3
d23=2×7+(-1) ×4+0×8=10
d24=2×3+(-1) ×(-2)+0×7=8
d31=4×1+5×2+1×(-2)=12
d32=4×0+5×(-3)+1×6=-9
d33=4×7+5×4+1×8=56
d34=4×3+5×(-2)+1×7=9
d41=3×1+(-4) ×2+(-2) ×(-2)=-1
d42=3×0+(-4) ×(-3)+(-2) ×6=0
d43=3×7+(-4) ×4+(-2) ×8=-11
d44=3×3+(-4) ×(-2)+(-2) ×7=3
d51=6×1+(-5) ×2+(-4) ×(-2)=4
d52=6×0+(-5) ×(-3)+(-4) ×6=-9
d53=6×7+(-5) ×4+(-4) ×8=-10
d54=6×3+(-5) ×(-2)+(-4) ×7=0.
Таким образом,  .
.
Пример 2. Найти значение многочлена f(x)=х3+3х2-2х от матриц А, В, С, если 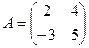 ,
, 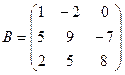 ,
, 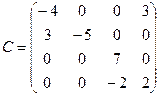 .
.
Решение.
- Найдем значение многочлена от матрицы А.
1) 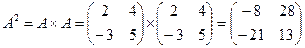 ;
;
2) 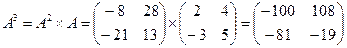 ;
;
3) 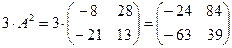 ;
;
4) 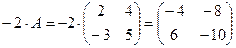 ;
;
5) 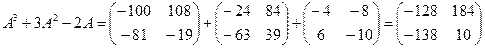 .
.
2. Найдем значение многочлена от матрицы В.
1) 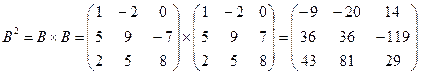 ;
;
2) 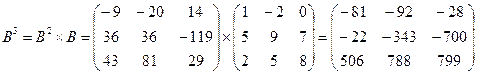 ;
;
3)  ;
;
4) 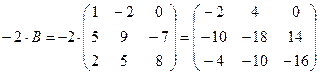 ;
;
5) 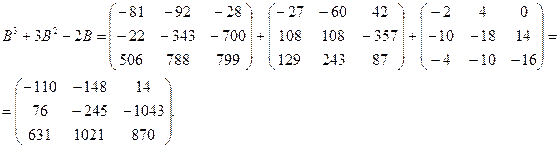
3. Найдем значение многочлена от матрицы С.
1) 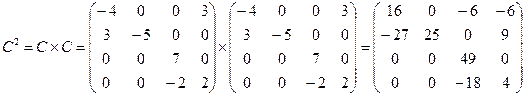 ;
;
2) 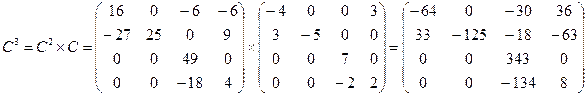 ;
;
3) 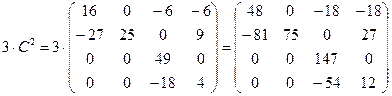 ;
;
4) 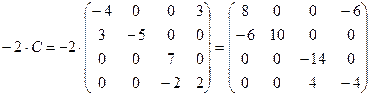
5) 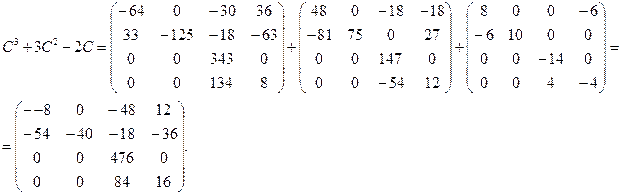
Ответ: 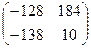 ;
; 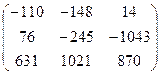 ;
; 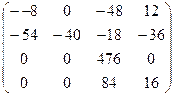 .
.
Пример 3.В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М1, М2 и М3, причем доставка единицы продукции с каждого молокозавода в магазин М1 стоит 50 ден. ед., в магазин М2 - 70, а в М3 - 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
| Молокозавод | Магазин | ||
| М1 | М2 | М3 | |
Решение. Обозначим через А матрицу, данную нам в условии, а через В - матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,
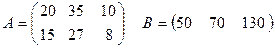 ,
, 
Тогда матрица затрат на перевозки будет иметь вид 
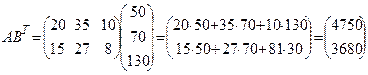 .
.
Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй - 3680 ден.ед.
Задания для аудиторного занятия
1.Найти матрицу 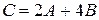 , если
, если 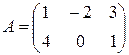 ,
, 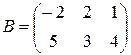 .
.
2.Заданы матрицы А, В, С. Найти произведения А´В, В´С, А´С, А´В´С.
2.1 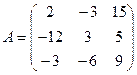 ,
, 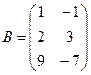 ,
,  ;
;
2.2. 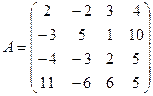 ,
, 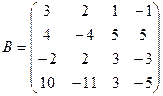 ,
,  .
.
3. Найти значение многочлена f(x)=х3+3х2-2х от матриц А, В, С, если 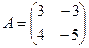 ,
, 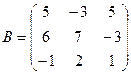 ,
, 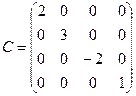 .
.
4. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется матрицей (вектором) X = (10, 15, 23). Используются ткани четырех типов Т1, Т2, Т3, Т4. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Матрица (вектор) С = (40, 35, 24, 16) задает стоимость метра ткани каждого типа, а матрица (вектор) P = (5, 3, 2, 2) - стоимость перевозки метра ткани каждого вида.
| Изделие | Расход ткани | |||
| Т1 | Т2 | Т3 | Т4 | |
| Зимнее пальто | ||||
| Демисезонное пальто | ||||
| Плащ |
Сколько метров ткани каждого типа потребуется для выполнения плана?
Домашнее задание
1.Найти матрицу Х если:
1.1. 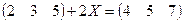 ;
;
1.2. 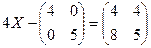 .
. 
2.Найти произведения матриц:
2.1.  ; 2.2.
; 2.2. 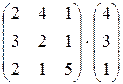 ;
;
2.3. 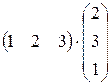 .
.
3.Вычислить 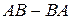 , если
, если 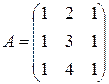 ,
, 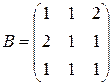 .
.
4. Найти значение многочлена f(x)=ху2+3х2 у-2ух от матриц Х, У, если
4.1.  ,
, 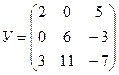 ;
;
4.2. 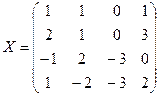 ,
,  .
.
5. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется матрицей (вектором) X = (10, 15, 23). Используются ткани четырех типов Т1, Т2, Т3, Т4. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Матрица (вектор) С = (40, 35, 24, 16) задает стоимость метра ткани каждого типа, а матрица (вектор) P = (5, 3, 2, 2) - стоимость перевозки метра ткани каждого вида.
| Изделие | Расход ткани | |||
| Т1 | Т2 | Т3 | Т4 | |
| Зимнее пальто | ||||
| Демисезонное пальто | ||||
| Плащ |
5.1. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
5.2.Определить стоимость всей ткани, необходимой для выполнения плана.
5.3.Подсчитать стоимость всей ткани с учетом ее транспортировки.
|
из
5.00
|
Обсуждение в статье: Пример выполнения заданий практической части |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

