Колебательность системы

Если корни характеристического уравнения системы , то

. (4.30)

Подобно тому как по заданным параметрам CAP определялась степень устойчивости h (и наоборот), можно определять значение колебательности m , при известных параметрах системы (и решать обратную задачу) [16].

Для этого в характеристическое уравнение системы вводится замена 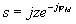, равноценная повороту мнимой оси на угол ( ), при этом пара сопряженных комплексных корней окажется на мнимой оси, а фиктивная система — на границе устойчивости. Колебательность m является оценкой переходного процесса сверху, при увеличении m возрастает число колебаний п за время регулирования и возрастает перерегулирование. Реальный переходной процесс может иметь значительно лучшее качество. Запишем смещенное характеристическое уравнение

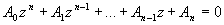, (4.31)

где

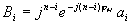. (4.32)

В (4.31) часть коэффициентов — комплексные числа. Поскольку фиктивная система находится на границе устойчивости, то (4.31) имеет пару сопряженных мнимых корней . Если в (4.31) вместо подставить и разделить смещенный характеристический полином на мнимую и действительную часть, то их можно поочередно приравнять нулю, получив при этом систему двух уравнений

.

Исключив из этой системы , получим искомое значение и .

4.6 Корневые годографы

Траектории, описываемые на комплексной плоскости корнями характеристического уравнения замкнутой системы при плавном изменении одного из ее параметров от 0 до ¥ , называют корневым годографом. Располагая корневым годографом, можно выбрать необходимое значение варьируемого параметра, соответствующее наиболее выгодному расположению корней с точки зрения требований к качеству конкретной системы.

В СССР основополагающими работами в этом направлении были работы К.Ф. Теодорчика , развитые Г. А. Бендриковым и С. П. Стрелковым в 1948—1949 гг., в США — работы В. Р. Ивенса в 1950 г.

Используя метод корневого годографа, можно решать следующие задачи : построения годографов полюсов передаточной функции замкнутой системы при изменении одного из ее параметров; оценки влияния параметров системы, появляющихся при ее усложнении; качественной и количественной оценки реакции системы на типовой сигнал при изменении значения параметра системы; синтеза корректирующих элементов системы. Для непрерывных линейных систем существует несколько методов построения корневых годографов, в частности, методы Ивенса, Теодорчика — Бендрикова и Удермана. Наименее нетрудоемким является метод Ивенса. Используя этот метод, можно оценить несколько вариантов с точностью 3—5%, что удобно на первом этапе проектирования. Метод Теодорчика — Бендрикова позволяет проводить более детальные расчеты с использованием ЭЦВМ.

Рассмотрим метод Ивенса. Передаточная функция замкнутой системы (рис. 4.14)

Рис. 4.14

(4.43)

где

(4.44)

передаточная функция разомкнутой системы.

Характеристическое уравнение замкнутой системы

(4.45)

или

. (4.46)

Нужно отметить, что излагаемый метод наиболее пригоден для выбора общего коэффициента k передаточной функции разомкнутой системы W(s), которая содержит его как множитель.

Уравнение (4.46) можно записать в виде системы уравнений относительно модулей и фаз

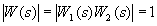; (4.47)

, (4.48)

где i=0,1,2,… .

Уравнение корневых годографов (4.48) является основой для их построения.

Пусть известны нули и полюсы передаточной функции разомкнутой системы: 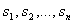—полюсы, — нули. Тогда передаточная функция разомкнутой системы

, (4.49)

где k — общий коэффициент усиления; а — множитель, появляющийся при разложении числителя и знаменателя W(s) на множители и т £ п.

Сомножители (двучлены) числителя и знаменателя функции (4.49) изображают на плоскости корней векторами , которые образуют с вещественной осью углы (рис. 4.15).

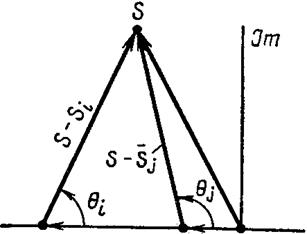
Рис. 4.15.

Тогда аргумент W(s) можно записать как разность аргументов числителя и знаменателя

и уравнение (4.48) примет вид:

. (4.50)

Уравнение (4.49) удобнее представить как или

, (4.51)

причем

,

где — длина соответствующих векторов.

Корневые годографы строят по (4.50), куда k не входит. Для уже найденных корней по (4.51) определяют k.

Построение корневых годографов требует знания их свойств, которые приведем ниже без доказательств.

1. Комплексные части корневых годографов попарно сопряжены и ветви годографа симметричны относительно вещественной оси.

2. Число ветвей корневого годографа равно порядку уравнения , т.е. числу полюсов передаточной функции замкнутой системы .

3. Ветви корневого годографа начинаются при k = 0 в полюсах передаточной функции разомкнутой системы W(s).

4. При т ветвей корневого годографа стремятся к т — нулям передаточной функции разомкнутой системы, а остальные (n — т) ветвей уходят в бесконечность.

5. (n— т) ветвей корневого годографа, уходящие в бесконечность, имеют асимптоты, число которых равно разности порядков числителя и знаменателя передаточной функции разомкнутой системы W(s), т.е. (n — т ). Асимптоты выходят из одной точки на вещественной отрицательной полуоси с абсциссой .