 |
Главная |
Встречно-параллельное соединение
|
из
5.00
|
На рисунке 5.26 представлен фрагмент ГЕРТ-сети, содержащей петлю, когда сигнал с выхода узла  подается на вход предшествовавшего узла
подается на вход предшествовавшего узла  .
.
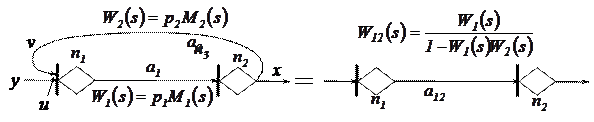
Рис. 5.26 Встречно-параллельное соединение дуг ГЕРТ-сети
Пусть на вход узла  приходит сигнал y , он складывается с сигналом обратной связи v, и сумма этих сигналов u проходит через дугу
приходит сигнал y , он складывается с сигналом обратной связи v, и сумма этих сигналов u проходит через дугу 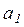 , в результате чего на выходе узла
, в результате чего на выходе узла 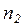 образуется выходной сигнал x. Но этот сигнал по дуге
образуется выходной сигнал x. Но этот сигнал по дуге 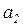 с передаточной функцией
с передаточной функцией 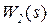 возвращается на вход узла
возвращается на вход узла 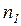 , превращаясь в v.
, превращаясь в v.
Учитывая свойство передаточных функций, получаем следующие соотношения между сигналами:
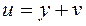 ,
, 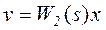 ,
, 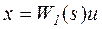 ,
,
откуда, исключая переменные u и v, получаем
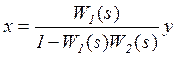 ,
,
то есть передаточная функция встречно-параллельного соединения равна

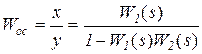 . (5.34)
. (5.34)
5.4.4 Модель процесса обучения как ГЕРТ-сеть
Проиллюстрируем возможности ГЕРТ-сетей на примере модели процесса интерактивного прохождения учебного курса.
Процесс заключается в следующем. Учащийся входит в обучающую систему и регистрируется в ней, после чего приступает к изучению разделов учебного курса. Изучив очередной раздел и выполнив контрольные задания, обучаемый переходит к изучению следующего раздела. Изучив все разделы, обучаемый получает возможность сдать экзамен. Если экзамен сдан с положительной оценкой, то процесс изучения курса считается успешно завершенным. В противном случае имеются две альтернативы: повторное изучение курса или отказ от дальнейшего обучения.
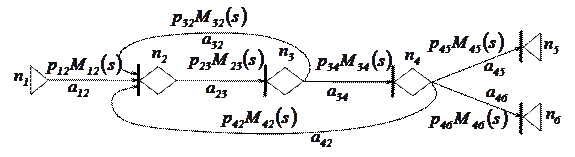
Рис. 5.27 ГЕРТ-сеть, моделирующая процесс обучения
Модель процесса в виде ГЕРТ-сети представлена на рисунке 5.27. Как видно из рисунка, эта сеть содержит множество узлов 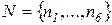 и множество A, содержащее 7 дуг, на которых выполняются следующие операции:
и множество A, содержащее 7 дуг, на которых выполняются следующие операции:
a12 ‑ вход и регистрация в обучающей системе;
a23 – изучение очередного раздела;
a32 – переход к изучению следующего раздела;
a34 – сдача экзамена;
a42 – переход к повторному изучению курса;
a45 – отказ от дальнейшего изучения;
a46 – успешное завершение курса.
Характеристики процессов, выполняемых на дугах (в часах), приводятся в таблице 5.4.
Таблица 5.4
Характеристики ГЕРТ-сети
| Название дуги | Вероятность выполнения | Тип распределения | Параметры распределения | Производящая функция 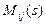
|
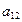
| Равномерное | 
| 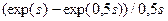
| |
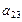
| Нормальное | 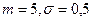
| 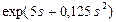
| |
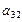
| 0,2 | Нормальное | 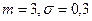
| 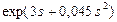
|
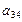
| 0,8 | Нормальное | 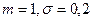
| 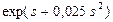
|
| 0,1 | Нормальное | 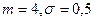
| 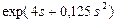
|
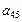
| 0,05 | Постоянная величина | 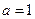
| 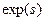
|
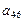
| 0,85 | Постоянная величина | 
| 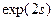
|
Выпишем выражения для передаточных функций 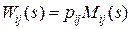 :
:
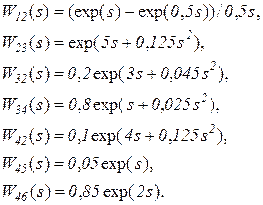 (5.35)
(5.35)
Составим передаточные функции 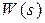 для рассматриваемой системы. Предварительно рассмотрим фрагмент сети, состоящий из узлов
для рассматриваемой системы. Предварительно рассмотрим фрагмент сети, состоящий из узлов 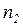 ,
, 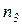 и дуг
и дуг 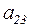 ,
, 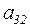 . Этот фрагмент образует соединение обратной связью, и в соответствии с формулой (5.34) его передаточная функция будет равна
. Этот фрагмент образует соединение обратной связью, и в соответствии с формулой (5.34) его передаточная функция будет равна
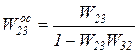 . (5.36)
. (5.36)
В результате схема ГЕРТ сети упростится и примет вид, показанный на рисунке 5.28.
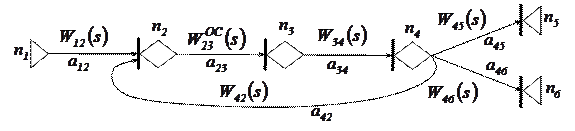
Рис.5.28 Преобразованная ГЕРТ-сеть.
Воспользуемся формулами (5.32) и (5.34) и получим передаточную функцию ГЕРТ-сети от узла  до узла
до узла  , что по условиям задачи соответствует успешному завершению курса:
, что по условиям задачи соответствует успешному завершению курса:
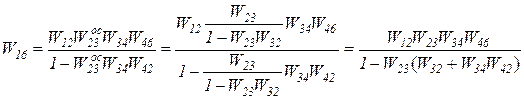 (5.37)
(5.37)
Подставив в формулу (5.37) выражения для передаточных функций всех дуг и проделав некоторые преобразования, получим
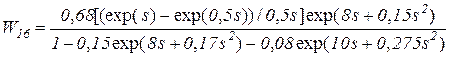 . (5.38)
. (5.38)
Для того, чтобы определить производящую функцию рассмотренной системы, воспользуемся формулой
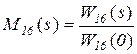 ,
,
которая следует из соотношений 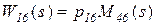 ,
, 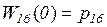 , т.к.
, т.к. 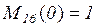 .
.
Из (5.38) следует 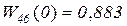 , следовательно, производящая функция системы имеет вид
, следовательно, производящая функция системы имеет вид
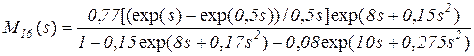 . (5.39)
. (5.39)
Перейдем теперь к вычислению моментов распределений сигнала 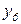 на выходе системы – поступившего по дуге
на выходе системы – поступившего по дуге 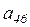 . В соответствии с формулой (5.28), вычислив производную
. В соответствии с формулой (5.28), вычислив производную 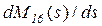 при
при 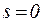 , получим оценку первого момента – математического ожидания
, получим оценку первого момента – математического ожидания
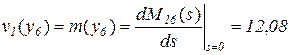 час.
час.
Далее, вычислив вторую производную 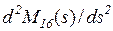 при
при 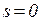 по формуле (4.28), получим второй момент распределения функции
по формуле (4.28), получим второй момент распределения функции 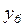 :
:
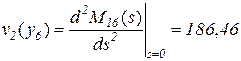 час2,
час2,
откуда
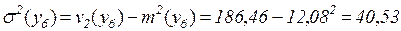 час2,
час2,
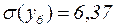 час. (5.40)
час. (5.40)
Таким образом, мы получили, что в данной системе среднее ожидаемое время успешного прохождения курса обучения составляет 12,08 часа, а среднеквадратичное отклонение от среднего равно 6,37 часа. Вероятность такого исхода равна 0,85/(0,85+0,05)=0,945.
Рассмотрим теперь цепочку узлов от  до
до 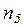 , что соответствует неудачному завершению процесса обучения. Эта цепочка отличается от рассмотренной ранее только последним звеном ‑
, что соответствует неудачному завершению процесса обучения. Эта цепочка отличается от рассмотренной ранее только последним звеном ‑ 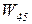 вместо
вместо 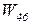 . Проделав выкладки, аналогичные приведенным выше, получим
. Проделав выкладки, аналогичные приведенным выше, получим
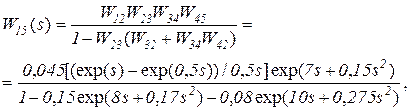
откуда
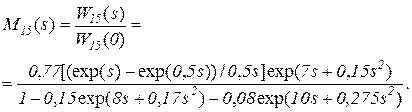 (5.41)
(5.41)
Вычислив первый и второй моменты случайной величины y5, получим
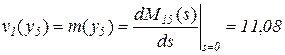 час,
час,
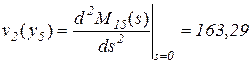 час2,
час2,
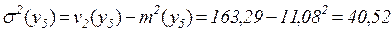 час2,
час2,  час.
час.
Итак, среднее время обучения при неудачном завершении курса составляет 11,08 часа, а среднеквадратичное отклонение от среднего равно 6,36 часа. Вероятность такого исхода равна 0,05/(0,85+0,05)=0,055.
Формулы для первой и второй производных функций 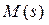 здесь не приводятся ввиду их громоздкости. Сложность аналитического вычисле-ния производных для систем реальной размерности требует либо примене-ния методов численного дифференцирования, либо использования систем символьных вычислений, которые в настоящее время получили доста-точное развитие и реализованы в пакетах MATHCAT и MATLAB [36].
здесь не приводятся ввиду их громоздкости. Сложность аналитического вычисле-ния производных для систем реальной размерности требует либо примене-ния методов численного дифференцирования, либо использования систем символьных вычислений, которые в настоящее время получили доста-точное развитие и реализованы в пакетах MATHCAT и MATLAB [36].
При численном дифференцировании задаются значениями параметра sв окрестности точки s=0 и малым шагом h. Например, вычислив значения функции 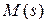 в точках
в точках 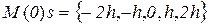 , можно затем по формулам численного дифференцирования оценить значения производных:
, можно затем по формулам численного дифференцирования оценить значения производных:
|
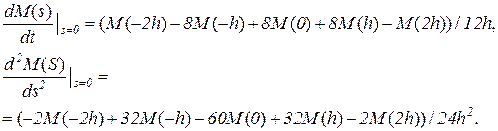
Аналогичным образом можно оценить и моменты функции распределения более высоких порядков.
Следует учесть, что для некоторых видов распределений (например, для бета-распределений 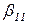 и
и 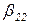 ) при вычислении
) при вычислении 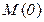 и
и 
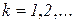 возникают неопределенности типа
возникают неопределенности типа 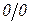 , а попытка определить эти функции численно по формулам вида (5.42) приводит к ошибке типа «деление на ноль». Поэтому такие неопределенности нужно либо устранять аналитически (например, по правилу Лопиталя), либо – причисленном определении производных – строить вычисление в окрестности нулевой точки таким образом, чтобы окрестность не включала саму эту точку.
, а попытка определить эти функции численно по формулам вида (5.42) приводит к ошибке типа «деление на ноль». Поэтому такие неопределенности нужно либо устранять аналитически (например, по правилу Лопиталя), либо – причисленном определении производных – строить вычисление в окрестности нулевой точки таким образом, чтобы окрестность не включала саму эту точку.
Располагая вычисленными моментами функции распределения выходной величины, можно затем оценить саму функцию распределения, задавшись ее видом [37]. Однако мы этот вопрос не рассматриваем.
|
из
5.00
|
Обсуждение в статье: Встречно-параллельное соединение |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

