 |
Главная |
Некоторые необходимые обозначения и определения
|
из
5.00
|
Федеральное государственное образовательное бюджетное
Учреждение высшего профессионального образования
«САНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ
Им. проф. М. А. БОНЧ-БРУЕВИЧА»
___________
П.З. Мкртычян.
МАТЕМАТИКА
ТЕОРИЯ ПРЕДЕЛОВ
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
ПО ВЫПОЛНЕНИЮ СОМОСТОЯТЕЛЬНОЙ РАБОТЫ
СПбГУТ )))
САНКТ-ПЕТЕРБУРГ
УДК
ББК
Рецензент
заведующий кафедрой Высшей математики ПГУПС
кандидат физ.-мат. наук, проф. Гарбарук В.В.
Утверждено редакционно-издательским советом СПбГУТ
в качестве методических указаний
| Мкртычян П.З. | |
| Математика. Теория пределов. Методические указания / П.З. Мкртычян . – СПб.: Издательство СПбГУТ, 2014. В методических указаниях подробно представлены необходимые теоретические положения теории пределов, в том числе, и правило Лопиталя раскрытия неопределённостей, подробно разобрано большое количество примеров. Методические указания содержат 25 вариантов контрольных работ на вычисление пределов. Данное издание можно использовать для самостоятельного освоения студентами-бакалаврами технических специальностей практической части указанного раздела высшей математики. |
УДК
ББК
© Мкртычян П.З. 2014
© Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «Санкт-Петербургский государственный университет телекоммуникаций им. проф. М. А. Бонч‑Бруевича».
-2-
Содержание
1.Некоторые необходимые обозначения и определения………………………………4
2.Определения пределов…………………………………………………………………………………6
3.Основные теоремы о пределах. Правила вычисления пределов……………….12
4.Непрерывные функции…………………………………………………………………………………14
5.Замечательные пределы……………………………………………………………………………….15
6.Сравнение бесконечно малых. Принцип эквивалентности…………………………17
7.Вычисление пределов…………………………………………………………………………………..19
8.Вычисление пределов по правилу Лопиталя……………………………………………….26
9.Варианты контрольных заданий…………………………………………………………………..29
10.Литература……………………………………………………………………………………………………41
-3-
Некоторые необходимые обозначения и определения.
Понятие предела является одним из основных понятий математического анализа.
Прежде, чем дать определение предела, приведём некоторые необходимые обозначения и определения.
Множество всех вещественных чисел будем обозначать через R. Следующие значки означают: 
 не принадлежит,
не принадлежит,  содержится,
содержится,
 любой,
любой,  существует,
существует,  следует,
следует,  тогда и только тогда. Заглавными буквами A,Bи т.д. будем обозначать множества вещественных чисел ( т.е. A
тогда и только тогда. Заглавными буквами A,Bи т.д. будем обозначать множества вещественных чисел ( т.е. A  , B
, B  ), а малыми буквами a, b и т.д. их элементы (a
), а малыми буквами a, b и т.д. их элементы (a  ).
).
Определение 1.1.  -окрестностью точки
-окрестностью точки  R называется множество
R называется множество  т.е. множество, состоящее из всех тех чисел
т.е. множество, состоящее из всех тех чисел  , которые удовлетворяют неравенству
, которые удовлетворяют неравенству  . Нетрудно понять, что
. Нетрудно понять, что  .
.
Определение 1.2.  -окрестностью «плюс бесконечности» (+
-окрестностью «плюс бесконечности» (+  называется множество
называется множество  =(
=( 
Определение 1.3.  -окрестностью «минус бесконечности» (
-окрестностью «минус бесконечности» ( 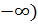 называется множество
называется множество  =(
=( 
Определение 1.4.  -окрестностью « бесконечности» (
-окрестностью « бесконечности» (  называется множество
называется множество  =(
=(  (
( 
Заметим, что предполагается  только в определении 1.1. Если в
только в определении 1.1. Если в 
Определение 1.5.Точка  называется внутренней точкой множества A
называется внутренней точкой множества A  , если она принадлежит множеству A вместе с некоторой своей
, если она принадлежит множеству A вместе с некоторой своей  -окрестностью.
-окрестностью.
Определение 1.6. Множество A называется открытым, если все его точки внутренние.
Пример 1.1.Всякий открытый интервал (a,b) является открытым множеством.
-4-
Определение 1.7.Окрестностью точки  называется всякий открытый интервал (a,b), содержащий точку
называется всякий открытый интервал (a,b), содержащий точку 
Заметим, что  -окрестность точки является также её окрестностью.
-окрестность точки является также её окрестностью.
Определение 1.8.Точка  называется граничной точкой множества A
называется граничной точкой множества A  , если всякая её окрестность содержит как точки, принадлежащие множеству A, так и не принадлежащие ему.
, если всякая её окрестность содержит как точки, принадлежащие множеству A, так и не принадлежащие ему.
Заметим, что граничная точка может принадлежать множеству, а может и не принадлежать ему.
Пример 1.2. Граничными точками множества A=  являются точки a и b, но точка a принадлежит множеству A, а b не принадлежит ему.
являются точки a и b, но точка a принадлежит множеству A, а b не принадлежит ему.
Определение 1.9.Объединение множества А с множеством его граничных точек называется замыканием множества А и обозначается  .
.
Определение 1.10. ЕслиА=  , то множество А называется замкнутым.
, то множество А называется замкнутым.
Пример 1.3. 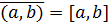 ,
,  ,
,  .
.
Определение 1.11. Точка  называется предельной точкой множества А, если любая её окрестность содержит точку множества А, отличную от точки
называется предельной точкой множества А, если любая её окрестность содержит точку множества А, отличную от точки  .
.
Заметим, что предельная точка множества может принадлежать этому множеству, а может и не принадлежать ему; точка, принадлежащая множеству, может не быть его предельной точкой.
Определение 1.12.Точка  называется изолированной точкой множества А, если она принадлежит множеству А и не является его предельной точкой.
называется изолированной точкой множества А, если она принадлежит множеству А и не является его предельной точкой.
Пример 1.4.Пусть А=(0,1)  . Предельными точками множества А являются только и только все точки интервала [0,1]; точка x=2 является изолированной точкой множества А.
. Предельными точками множества А являются только и только все точки интервала [0,1]; точка x=2 является изолированной точкой множества А.
Пример 1.4.Все точки множества натуральных чисел N={1,2,3,…} являются изолированными. У множества N есть только одна предельная точка + 
-5-
Определения пределов.
Пусть задана числовая функция 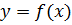 с областью определения А
с областью определения А  и
и
 - предельная точка множества А. В этом параграфе будут приведены определения предела
- предельная точка множества А. В этом параграфе будут приведены определения предела  функции
функции  при
при  , стремящемся к
, стремящемся к  . На интуитивном уровне должно быть понятно, что это означает, что при приближении
. На интуитивном уровне должно быть понятно, что это означает, что при приближении  к
к  значение функции становится сколь угодно близким к
значение функции становится сколь угодно близким к 
Например, нетрудно догадаться, что при  , стремящемся к 3 пределом функции
, стремящемся к 3 пределом функции  должно быть число 9=
должно быть число 9=  .
.
Определение 2.1. Пусть  - предельная точка области определения А функции
- предельная точка области определения А функции  (всюду ниже будем это предполагать, не оговаривая особо). Тогда
(всюду ниже будем это предполагать, не оговаривая особо). Тогда  называется пределом функции
называется пределом функции  при
при  , стремящемся к
, стремящемся к  , (это обозначается так:
, (это обозначается так:  ), если для
), если для  (любой)
(любой)  -окрестности
-окрестности  (существует) такая
(существует) такая  -окрестность
-окрестность  точки
точки  что из того, что
что из того, что  ,
,  следует, что)
следует, что)  .
.
Замечание 2.1.Если в приведённом определении  - и
- и  -окрестности заменить на окрестности точек
-окрестности заменить на окрестности точек  и
и  соответственно, то получится определение, эквивалентное приведённому.
соответственно, то получится определение, эквивалентное приведённому.
Замечание 2.2.В приведённом определении каждая из величин  и
и  может быть как конечной, так и равной +
может быть как конечной, так и равной +  т.е. оно содержит шестнадцать определений предела.
т.е. оно содержит шестнадцать определений предела.
Приведённое определение называется определением предела на языке окрестностей.
Учитывая то, какими неравенствами описываются  - и
- и  -окрестности конечных точек и бесконечностей, приведём теперь все шестнадцать определений пределов на так называемом языке
-окрестности конечных точек и бесконечностей, приведём теперь все шестнадцать определений пределов на так называемом языке  ,
,  эквивалентные определению 2.1. Некоторые из них проиллюстрируем рисунками.
эквивалентные определению 2.1. Некоторые из них проиллюстрируем рисунками.
Всюду ниже величины  и
и  предполагаются конечными.
предполагаются конечными.
Определение 2.2.Говорят, что  , если для
, если для 

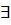
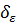 такое, что из того, что
такое, что из того, что 

 .
.
-6-
Запись « 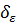 » означает, что
» означает, что  зависит от
зависит от  . Всюду ниже мы для краткости
. Всюду ниже мы для краткости
будем писать просто 

Рис.1
Заштрихованный интервал на оси OY  это окрестность
это окрестность 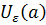 , которая описывается неравенством
, которая описывается неравенством  , а заштрихованный интервал на оси OX
, а заштрихованный интервал на оси OX  это окрестность
это окрестность  которая описывается неравенством
которая описывается неравенством 
Пример 2.1.  .
.
Для произвольного достаточно малого  решением неравенства
решением неравенства  будет интервал, описываемый неравенством
будет интервал, описываемый неравенством  , или
, или 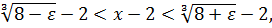 откуда видно, что если положить
откуда видно, что если положить  , то из того, что
, то из того, что 
 .
.
Определение 2.3.Говорят, что  , если для
, если для 

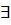
 такое, что из того, что
такое, что из того, что 

 .
.

Рис.2
-7-
Заштрихованный интервал на оси OY  это окрестность
это окрестность  , которая описывается неравенством
, которая описывается неравенством  , а заштрихованный интервал на оси OX
, а заштрихованный интервал на оси OX  это окрестность
это окрестность  которая описывается неравенством
которая описывается неравенством 
Пример 2.2. 
Действительно, для 
 неравенство
неравенство  выполнено, как только
выполнено, как только  , если
, если  ; если же
; если же  , то
, то  при любом
при любом 
Определение 2.4.Говорят, что  , если для
, если для 

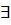
 такое, что из того, что
такое, что из того, что 

 .
.
Иллюстрацией определения 2.4 является зеркальное отражение рисунка 2 относительно оси OX.
Пример 2.3.Очевидно, что 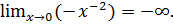
Определение 2.5.Говорят, что  , если для
, если для 

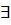
 такое, что из того, что
такое, что из того, что 

 .
.

Рис.3
Заштрихованное множество на оси OY 
 это окрестность
это окрестность  , которая описывается неравенством
, которая описывается неравенством 
 , а заштрихованный интервал на оси OX
, а заштрихованный интервал на оси OX  это окрестность
это окрестность  которая описывается неравенством
которая описывается неравенством  Заметим, что если
Заметим, что если
 ,то
,то 
 R.
R.
-8-
Определение 2.6.Говорят, что 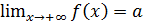 , если для
, если для 

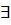
 такое, что из того, что
такое, что из того, что 

 .
.

Рис.4
На осях OY и OX заштрихованы соответственно интервалы  и (
и (  . Это соответственно окрестности
. Это соответственно окрестности 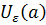 и
и  , которые описываются неравенствами
, которые описываются неравенствами  и
и  .
.
Пример 2.4. 
Действительно, для 
 неравенство
неравенство  , как только
, как только  .
.
Определение 2.7.Говорят, что  , если для
, если для 

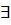
 такое, что из того, что
такое, что из того, что 

 .
.

Рис.5
Заштрихованные на осях OX и OY множества – это  и (
и (  =
=  .
.
Определение 2.8.Говорят, что  , если для
, если для 

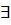
 такое,
такое,
-9-
что из того, что 


Иллюстрацией определения 2.8 является зеркальное отражение рисунка 5 относительно оси ОХ.
Пример 2.5.  .
.
Действительно, для 
 из того, что
из того, что  =
=  ,
, 
Определение 2.9.Говорят, что  , если для
, если для 

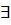
 такое, что из того, что
такое, что из того, что 

 .
.
Пример 2.6.Пусть  , если
, если  рациональное, и
рациональное, и  , если
, если  рациональное. Очевидно, что
рациональное. Очевидно, что  , так как для
, так как для 
 из того, что
из того, что  =
=  .
.
Определение 2.10.Говорят, что  , если для
, если для 

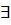
 такое, что из того, что
такое, что из того, что 

 .
.
Иллюстрацией определения 2.10 является зеркальное отражение рисунка 4 относительно оси ОY.
Пример 2.7. 
Определение 2.11.Говорят, что  , если для
, если для 

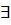
 такое, что из того, что
такое, что из того, что 

 .
.
Иллюстрацией определения 2.11 является зеркальное отражение рисунка 5 относительно оси ОY.
Определение 2.12.Говорят, что  , если для
, если для 

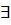
 такое, что из того, что
такое, что из того, что 

 .
.
Иллюстрацией определения 2.12 является зеркальное отражение рисунка 5 относительно осей ОY и ОХ.
Пример 2.8.  .
.
Определение 2.13.Говорят, что  , если для
, если для 

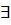
 такое, что из того, что
такое, что из того, что 

 .
.
-10-
Пример 2.9.Для функции  , рассмотренной в примере 2.6, имеем:
, рассмотренной в примере 2.6, имеем:  .
.
Определение 2.14.Говорят, что  , если для
, если для 

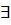
 такое, что из того, что
такое, что из того, что 

 .
.
Нетрудно понять, что 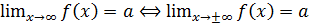 .
.
Пример 2.10.  (см. примеры 2.4 и 2.7).
(см. примеры 2.4 и 2.7).
Определение 2.15.Говорят, что 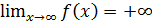 , если для
, если для 

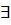
 такое, что из того, что
такое, что из того, что 

 .
.
Определение 2.16.Говорят, что  , если для
, если для 

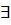
 такое, что из того, что
такое, что из того, что 

 .
.
Опять же, 

Пример 2.11.  .
.
Определение 2.17.Говорят, что  , если для
, если для 

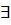
 такое, что из того, что
такое, что из того, что 

 .
.
Очевидно, что 
Пример 2.12.Для функции  , рассмотренной в примере 2.6, имеем:
, рассмотренной в примере 2.6, имеем:  .
.
Приведём теперь определения односторонних пределов.
Определение 2.18.  называется левосторонним (правосторонним) пределом функции
называется левосторонним (правосторонним) пределом функции  при
при  , стремящемся к
, стремящемся к  слева (справа), если для
слева (справа), если для 

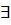
 такое, что из того, что
такое, что из того, что 

 .
.
Левосторонний и правосторонний пределы обозначаются соответственно
 и
и  .
.
Определение 2.19.Говорят, что  (
( 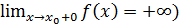 , если для
, если для 

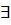
 такое, что из того, что -11-
такое, что из того, что -11-


 .
.
Определение 2.20.Говорят, что  , (
, (  , если для
, если для 

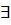
 такое, что из того, что
такое, что из того, что 

 .
.
Определение 2.21.Говорят, что  , (
, (  , если для
, если для 

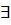
 такое, что из того, что
такое, что из того, что 


Пример 2.13.Нетрудно понять, что 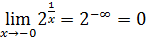 ,
,  .
.
Справедлива следующая
Теорема 2.1 (о единственности предела).Если  и
и  , то
, то  .
.
Нетрудно убедиться, что справедлива следующая
Теорема 2.2.  .
.
|
из
5.00
|
Обсуждение в статье: Некоторые необходимые обозначения и определения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

