Сравнение бесконечно малых. Принцип эквивалентности

Определение 6.1.Бесконечно малые и называются бесконечно малыми одного порядка, если

Определение 6.2.Бесконечно малые и называются эквивалентными ( , если

Определение 6.3.Бесконечно малая называется бесконечно малой высшего порядка (по сравнению с бесконечно малой , если

-17-

Теорема 6.1.Если и - эквивалентные бесконечно малые, то

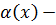
- бесконечно малая высшего порядка по сравнению с каждой из них.

Теорема 6.2.Если - бесконечно малая высшего порядка по сравнению с , то .

Теорема 6.3 (принцип эквивалентности).Если и - эквивалентные бесконечно малые, то .

Т.е., если под знаком предела бесконечно малая входит как сомножитель, то ее можно заменить на эквивалентную.

Замечание 6.1.Особо заметим, что этого нельзя делать в разностях и суммах.

Из первого, третьего, четвёртого и пятого замечательных пределов и их следствий вытекает следующая таблица эквивалентности для бесконечно малых:

(6.1)

tg (6.2)

rcsin (6.3)

rctg (6.4)

(6.5)

(6.6)

(6.7)

(6.8)

(6.9)

(6.10)

-18-

Докажем (6.10). Для этого посчитаем предел . Этот предел представляет из себя неопределённость вида Для того, чтобы его посчитать, нужно воспользоваться формулой и тем, что . Тогда получим: , откуда следует (6.10).

Вычисление пределов.

В этом разделе рассмотрим ряд типовых задач на вычисление пределов.

Пример 7.1. .

Предел 7.1 представляет из себя неопределённость вида ( всюду ниже, чтобы указать вид неопределённости, мы будем просто приравнивать предел к соответствующему обозначению неопределённости).

Для вычисления подобных пределов нужно числитель и знаменатель дроби разделить на старшую степень, а затем воспользоваться теоремами 3.7, 3.3 и 3.4. Имеем:

.

Пример 7.2.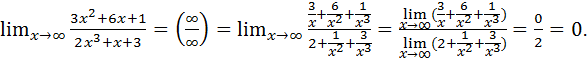

Пример 7.3.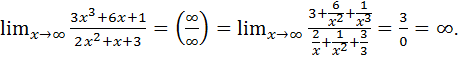

Здесь используется, что величина, обратная бесконечно малой является бесконечно большой (теорема 3.3).

Заметим, что пределы 7.2 и 7.3 можно было бы посчитать и несколько иначе:

-19-

Проанализировав решения примеров7.1 – 7.3, нетрудно понять, что справедлива следующая

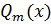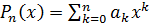Теорема 7.1.Пусть и – многочлены степеней соответственно, т.е. , , , Пусть Тогда: 1) если ; 2) если

3) если

Рассмотрим теперь пределы отношений многочленов при , стремящемся к конечному числу.

Пример 7.4. .

В силу теорем 4.1 и 4.2 рассматриваемая функция является непрерывной. Это означает, что .

Пример 7.5. .

Положив , получим, что

Пример 7.6. .

Положив , получим, что

Пример 7.7. .

Положив , получим, что , т.е., в отличие от пределов 7.4 – 7.6, предел 7.7 является неопределённостью вида То, что при числитель и знаменатель дроби обращаются в нуль, означает. Что каждый из них разлагается на множители, один из которых равен Найдя корни

-20-

числителя и знаменателя, разложив последние на множители, получим:

.

Пример 7.8. .

Положив , получим, что Разложим числитель по формуле разности кубов. Для разложения на множители знаменателя разделим его на . Тогда получим:

.

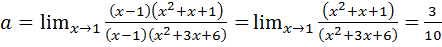Пример 7.9. .

Положив , получим: Для раскрытия этой неопределённости нужно умножить числитель и знаменатель дроби на выражение, сопряжённое числителю, т.е. на 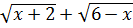, и разложить знаменатель на множители:

.

Пример 7.10.

Для раскрытия неопределённости умножим числитель и знаменатель дроби на и разложим знаменатель на множители. Тогда получим:

.

-21-

Пример 7.11.

Разложив знаменатель на множители и умножив числитель и знаменатель на , в силу формулы разности кубов получим:

.

Пример 7.12. .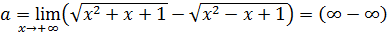

Для раскрытия неопределённости 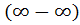умножим и разделим на сопряженное выражение . Тогда получим:

.

Разделив числитель и знаменатель на получим:

Пример 7.13. .

Заметим, что этот предел не имеет ничего общего с первым замечательным пределом (5.1). Поскольку , а – бесконечно малая при , то

Перейдём теперь к пределам, при вычислении которых используются замечательные пределы или, что то же самое, таблица эквивалентности.

Пример 7.14.

-22-

Сначала особо заметим, что если в разности, стоящей в числителе предела

 

7.14, и заменить на эквивалентную бесконечно малую величину , то получится неверный ответ

Для получения правильного ответа нужно положить , затем вынести за скобки, тогда в силу (6.1) и (6.10) получим:

.

Пример 7.15. .

Поделив числитель и знаменатель дроби на , в силу (6.3) и (6.4) получим:

.

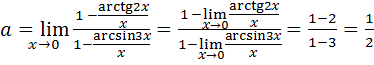Заметим, что если в пределе 7.15 и заменить на эквивалентные бесконечно малые , то получится правильный ответ. Но такое решение будет неверным, так как нет теоремы, на которую можно сослаться.

Пример 7.16. .

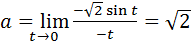Для раскрытия неопределённости нужно разность в числителе преобразовать в произведение. Кроме того, поскольку в замечательных пределах (кроме второго в одном из видов) стремится к нулю, то удобно ввести новую переменную Тогда Тогда , откуда получим: . -23-

Пример 7.17.

Поскольку 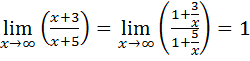, то предел 7.17 является неопределённостью вида 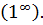Воспользовавшись логарифмическим тождеством , представим основание в виде .Тогда .

Воспользовавшись непрерывностью экспоненты (см. определение 4.1 и теорему 4.1) и тем, что если , то и, следовательно, (см. (6.5)), получим:

.

С помощью выкладок, используемых при вычислении предела 7.17, может быть доказана

Теорема 7.2.Пусть 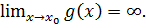Тогда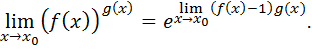

Действительно, так как то и при . Тогда

Все неопределённости вида раскрываются по теореме 7.2.

Пример 7.18. .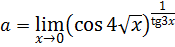

Так как , tg то Тогда

.

-24-

 

Поскольку и , tg3 , то

. Следовательно, .

Пример 7.20. .

.

Поскольку (см. (6.7), (6.2), (6.10)), то

.

Пример 7.21. .

Поскольку при (см. (6.5) и (6.4)), то = 2.

Пример 7.22. .

Поскольку ,

, то

Заметим, что писать сначала , а затем

некорректно, так как не сформулированы соответствующие теоремы, на которые можно было бы сослаться. По той же причине недопустимо писать сначала , а затем

-25-