 |
Главная |
Дисперсия дискретной случайной величины
|
из
5.00
|
Математическое ожидание не дает полной характеристики закона распределения случайной величины.
Например, пусть заданы две дискретные случайные величины Х и У своими законами распределения:
| Х | -2 | У | -100 | |||||
| Р | 0,4 | 0,2 | 0,4 | Р | 0,3 | 0,4 | 0,3 |
Несмотря на то, что математические ожидания Х и У одинаковы М(Х)=М(У)=0, возможные значения Х и У «разбросаны» или «рассеяны» около своих математических ожиданий по-разному: возможные значения величины Х расположены гораздо ближе к своему математическому ожиданию, чем значения величины У.
При одинаковой средней величине годовых осадков одна местность может быть засушливой и неблагоприятной для сельскохозяйственных работ (нет дождей весной и летом), а другая благоприятной для ведения сельского хозяйства.
Значит, возникает необходимость введения новой числовой характеристики случайной величины, по которой можно судить о «рассеянии» возможных значений этой случайной величины.
Пусть задана дискретная случайная величина Х:
Определение 1. Отклонением случайной величины Х от ее математического ожидания М(Х) (или просто отклонением случайной величины Х) называют случайную величину Х-М(Х).
Для того чтобы отклонение случайной величины Х приняло значение 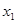 -М(Х), достаточно, чтобы случайная величина Х приняла значение
-М(Х), достаточно, чтобы случайная величина Х приняла значение 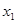 .
.
Вероятность этого события равна 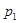 , значит и вероятность того, что отклонение случайной величины Х примет значение
, значит и вероятность того, что отклонение случайной величины Х примет значение 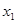 -М(Х), также равна
-М(Х), также равна 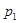 . Используя это, запишем закон распределения отклонения случайной величины Х :
. Используя это, запишем закон распределения отклонения случайной величины Х :
| Х - М(Х) | 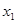 - М(Х) - М(Х)
| 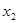 - М(Х) - М(Х)
| … |  - М(Х) - М(Х)
|
| р | 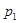
| 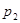
| … | 
|
Вычислим математическое ожидание отклонения Х-М(Х), получим: М(Х-М(Х))=М(Х)-М(Х)=0.
Справедлива следующая теорема:
Теорема.Математическое ожидание отклонения Х-М(Х) равно нулю.
Из теоремы видно, что с помощью отклонения не удается определить среднее отклонение возможных значений величины Х от ее математического ожидания, т.е. степень рассеяния величины Х.
Запишем закон распределения случайной величины (Х-М(Х))2 ( рассуждая аналогично, как и в случае случайной величины Х-М(Х) ).
| (Х-М(Х))2 | ( 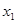 -М(Х))2 -М(Х))2
| ( 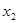 -М(Х))2 -М(Х))2
| … | (  -М(Х))2 -М(Х))2
|
| р | 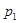
| 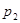
| … | 
|
Определение. Дисперсией D(X) дискретной случайной величины Х называют маиематическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания: D(X)= (Х-М(Х))2.
Из закона распределения величины (Х-М(Х))2 следует, что  Свойства дисперсии дискретной случайной величины
Свойства дисперсии дискретной случайной величины
1. Дисперсия дискретной случайной величины Х равна разности между математическим ожиданием квадрата величины Х и квадратом ее математического ожидания: D(X)=M(X2)-M2(X).
С помощью этого свойства и свойств математического ожидания устанавливаются следующие свойства:
2. Дисперсия постоянной величины С равна нулю.
3. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:  .
.
4. Дисперсия суммы двух независимых величин равна сумме дисперсий этих величин: D(X+Y)=D(X)+D(Y).
Методом математической индукции это свойство распросраняется и на случай любого конечного числа слагаемых. Следствием свойств 3 и 4 является свойство 5.
5. Дисперсия разности двух независимых величин Х и У равна сумме их дисперсий: D(X-Y)=D(X)+D(Y).
Определение. Средним квадратическим отклонением  (Х) Случайной величины Х называется корень квадратный из дисперсии:
(Х) Случайной величины Х называется корень квадратный из дисперсии:  (Х)=
(Х)=  .
.
Т.к. дисперсия измеряется в квадратных единицах относительно размерности самой случайной величины, то в тех случаях, когда нужно иметь числовую характеристику рассеяния возможных значений в той же размерности, что и сама случайная величина и используют среднее квадратическое отклонение.
|
из
5.00
|
Обсуждение в статье: Дисперсия дискретной случайной величины |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

