 |
Главная |
Функция необратимая на области определения
|
из
5.00
|
Тригонометрические функции.
Тригонометрические уравнения и неравенства.
Свойства и графики тригонометрических функций.
Определение: Тригонометрической функцией числового аргумента х называется тригонометрическая функция угла, содержащего х радиан.
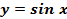 ,
, 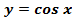 ,
, 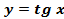 ,
,  .
.
Свойства и график тригонометрической функции 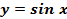 .
.
| x |
| y |
| у = 1 |
| у = - 1 |
| y |
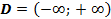 .
.
2. Множество значений функции: 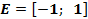
Вывод: График функции расположен между прямыми y = -1 ; y = 1 .
3. Функция нечетная, то есть 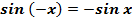 .
.
Вывод: График функции симметричен относительно начала координат.
4. Функция периодическая, так как 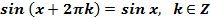 .
.
Вывод:График функции повторяется через 2p.
5. Функция не монотонная:
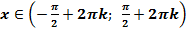
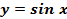 возрастает от-1до 1 ;
возрастает от-1до 1 ;
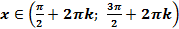
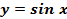 убывает от 1 до-1 .
убывает от 1 до-1 .
Функция необратимая на области определения.
7. y = 0; sin x = 0 при x = pk -нули функции.
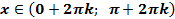
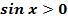
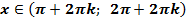
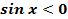
8. Функция ограниченная, так как 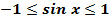 .
.
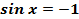 при
при 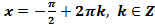
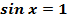 при
при 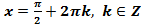
| x |
| y |
| -1 |
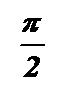
|
| p |
| 2p |
| - p |
| - 2p |
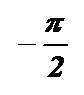
|
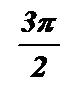
|
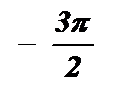
|
График функции 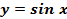 называется синусоидой.
называется синусоидой.
| x |
| y |
| у = 1 |
| у = - 1 |
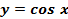 .
.
1. Область определения функции: 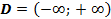 ) .
) .
2. Множество значений функции: 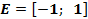 .
.
Вывод: График функции расположен между прямыми y = -1 ; y = 1 .
3. Функция четная, то есть 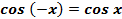
Вывод: График функции симметричен относительно оси ординат.
4. Функция периодическая, так как 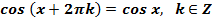 .
.
Вывод:График функции повторяется через 2p.
5. Функция не монотонная:
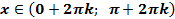
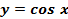 убывает от 1 до- 1;
убывает от 1 до- 1;
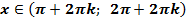
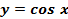 возрастает от- 1 до 1 .
возрастает от- 1 до 1 .
Функция необратимая на области определения.
7. y = 0; 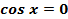 при
при 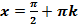 .
.
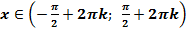
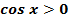
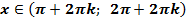
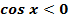
8. Функция ограниченная, так как 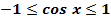 .
.
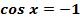 при
при 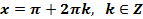 ,
,
| x |
| y |
| -1 |
| p |
| 2p |
| - p |
| -2p |
|
|
|
|
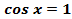 при
при 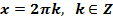
График функции 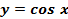 называется косинусоидой.
называется косинусоидой.
Свойства и график тригонометрической функции 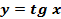 .
.
1. Область определения функции: 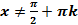 или
или 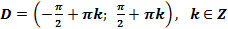 .
.
2. Множество значений функции: 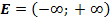 .
.
Вывод: График функции расположен между прямыми 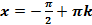 ,
, 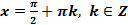 .
.
3. Функция нечетная, то есть 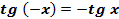 .
.
Вывод: График функции симметричен относительно начала координат.
4. Функция периодическая, так как как tg ( x + pk ) = tg x , k ÎZ.
Вывод:График функции повторяется через p.
5. Функция не монотонная на всей области определения, но функция возрастающая в каждом из промежутков 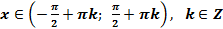 .
.
Функция необратимая на области определения.
7. 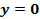 ;
; 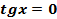 при
при 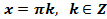 -нули функции.
-нули функции.
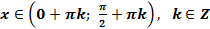
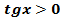
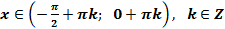
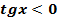
8. Функция неограниченная, так как 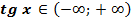 .
.
График функции 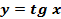 называется тангенсоидой.
называется тангенсоидой.
| y |
| x |
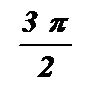
|
| p |
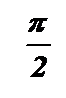
|
| -1 |
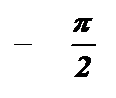
|
| - p |
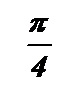
|
|
|
|
|
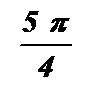
|
Свойства и график тригонометрической функции  .
.
1. Область определения функции: 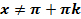 или
или 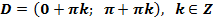 .
.
2. Множество значений функции: 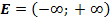 .
.
Вывод: График функции расположен между прямыми 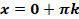 ,
, 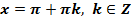 .
.
3. Функция нечетная, то есть 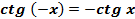 .
.
Вывод: График функции симметричен относительно начала координат.
4. Функция периодическая, так как сtg ( x + pk ) = сtg x , k ÎZ.
Вывод:График функции повторяется через p.
5. Функция не монотонная на всей области определения, но функция убывающая в каждом из промежутков xÎ( 0+pk ; p+pk ) , k ÎZ.
6. Функция необратимая на области определения.
7. y = 0; 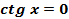 при
при 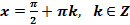 -нули функции.
-нули функции.
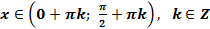
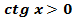
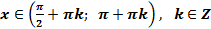
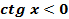
8. Функция неограниченная, так как 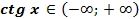 .
.
График функции  называется котангенсоидой.
называется котангенсоидой.
| x |
| y |
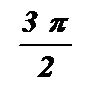
|
| p |
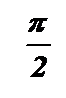
|
| -1 |
|
| - p |
|
|
|
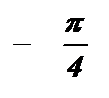
|
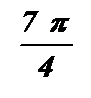
|
| 2 p |
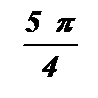
|
|
из
5.00
|
Обсуждение в статье: Функция необратимая на области определения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

