Неопределенный интеграл. Интегрирование по частям

Понятие неопределенного интеграла. Основные свойства

Определение1: Функция на заданном промежутке называется первообразной для функции , если во всем промежутке , является производной для . .

Определение2: Если для функции существует первообразная на промежутке , то множество первообразных на называется неопределенным интегралом от и обозначается

Теорема: Если первообразная для на , то выражение даёт множество всех первообразных для функции на .

Из определения и теоремы получается, что .

подынтегральная функция.

подынтегральное выражение. х- переменная интегрирования.

Непосредственно из определения интеграла вытекают следующие свойства:

1)

2)

3) При существовании конечной производной справедливо, что

4)

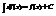
Задача: Пусть задано ускорение, как функция от времени . Пусть a=g . Зададим начальные условия, для того, чтобы получить конкретное решение задачи: Пусть в имелась , подставим их в (1). Получаем . Пусть 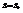, ; , Получаем, что

Основные свойства и правила вычисления неопределенного интеграла.

1) Свойства интегралов

1) Свойство однородности интеграла относительно подынтегральной функции ,

2) Свойство аддитивности:

 

 

Замена переменной в неопределенном интеграле

Теорема1: (первый вариант замены переменной)

Пусть надо вычислить , если функция дифференцируема на и на промежутке , тогда , на .

Формула (1) получается в случае, если вместо мы вводим переменную , дифференцируя это равенство получаем

Теорема2: (второй вариант замены)

Пусть надо вычислить интеграл , если функция дифференцируема на и на , то

 

В формуле (2) мы формально вводим новую функцию: ,

Неопределенный интеграл. Интегрирование по частям

Пусть имеют непрерывные производные, тогда по правилу дифференцирования производной получим , , для первообразной будет , поэтому имеет место формула (получаемая интегрированием (*)) , которая выражает правило интегрирования по частям, оно приводит интегрирование выражения 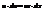к интегрированию выражения

Таким образом, применяя формулу (3) к вычислениям, придется разбивать подынтегральное выражение на 2 множителя, из которых первый дифференцируется , а второй интегрируется при переходе к интегралу правой части. Данное правило имеет более ограниченную область применения, чем замена переменной, но есть целые классы интегралов, которые берутся интегрированием по частям.

К ним относятся:

1)

2)

3)

Интегрирование в конечном виде

Производная любой элементарной функции, снова есть элементарная функция.

Интеграл рациональной функции, как правило, не является рациональной функцией.

Подобным образом, интеграл любой рациональной функции, как правило, не является элементарной, т.е. не может быть выполнен с помощью конечного числа арифметических операций и композиций (т.е. не выражается в конечном виде).

Например:

- не берущиеся интегралы, не выражаются конечными функциями.

Но, тем не менее, для каждой непрерывной функции интеграл берется и является непрерывной функцией.

Общего алгоритма для выражения неопределенного интеграла не существует, поэтому становится важным выделить элементарные функции, интеграл от которых снова есть элементарная функция, и выделить классы таких функций, составить алгоритм для их интегрирования.