 |
Главная |
Основная формула интегрального исчисления.
|
из
5.00
|
Пусть f(x) непрерывна на [a,b], тогда  будет являться первообразной функцией для f(x), т.к. (
будет являться первообразной функцией для f(x), т.к. (  ). Если теперь F(x) любая первообразная для f(x), то
). Если теперь F(x) любая первообразная для f(x), то  . Для определения с(const).
. Для определения с(const). 

x=b  (*)
(*)
Формула Ньютона-Лейбница. Основная формула интегрального исчисления.
Значение о.и. выражается разностью двух значений при x=a и x=b. Если применить теорему о среднем и учтем, что 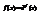 , то получим, что
, то получим, что

Получили формулу для конечных приращений Лагранжа для F(x). Таким образом, основная формула (*) устанавливает связь между теоремой о среднем, дифференциальным и интегральным исчислении.
Замена переменной в определенном интеграле. Интегрирование по частям.
Пусть надо вычислить  , где f(x) непрерывная на [a,b] функция. Положим
, где f(x) непрерывная на [a,b] функция. Положим  . Причем функцию
. Причем функцию  наложим условие.
наложим условие.  должна быть непрерывна на промежутке
должна быть непрерывна на промежутке
1) 
2) 
3)  на
на 
Тогда справедлива формула
(1) 
Т.к. по предположению подынтегральная функция непрерывна , то существует и соответствующие неопределенные интегралы слева и справа в (1) и можно воспользоваться основной формулой (*).
Причем, если F(x)- первообразная функции f(x), то  , то первообразная
, то первообразная  .
.
Замечание. В отличие от замены в неопределенном интеграле, здесь не надо возвращаться к первой переменной x. Т.к., если вычислим второй интеграл по t, представляют собой число, то тем самым вычислим и первый интеграл.
Интегрирование по частям.

Приложения определенного интеграла: вычисление площади плоской фигуры.
Вычисление площадей. 
а)  и непрерывна, тогда площадь криволинейной трапеции
и непрерывна, тогда площадь криволинейной трапеции 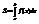
б) x=a, x=b и y=f(x), y=g(x);  на [a,b]
на [a,b]

Замечание : 

в) Пусть кривая задана параметрическим уравнением.
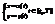
В данном случае мы не знаем явного задания кривой, поэтому при вычислении площади делаем замену, что бы свести к известным формулам.

x(t)-убывает

Пример(Вычислить площадь фигуры)


Вычисление площади в полярной системе координат.
 Если линия, ограничивающая фигуру, задана в полярной системе координат, то в качестве основной фигуры принимает криволинейный сектор, то есть фигуру ограниченную
Если линия, ограничивающая фигуру, задана в полярной системе координат, то в качестве основной фигуры принимает криволинейный сектор, то есть фигуру ограниченную 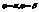 и графиком
и графиком 
Разобьем  (а вместе с ним и весь сектор)на частичные сектора
(а вместе с ним и весь сектор)на частичные сектора 
Каждый частичный сектор заменим круговым сектором. То есть будем считать, что на каждом из частичных промежутков  функция
функция  изменится мало и приблизительно равна
изменится мало и приблизительно равна 


Тогда, площадь фигуры, состоит из круговых секторов, каждый из которых имеет площадь  ,будет равна
,будет равна  .
.
Устремив  и переходя к пределу, получаем
и переходя к пределу, получаем 
|
из
5.00
|
Обсуждение в статье: Основная формула интегрального исчисления. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

