Отношение делимости и его свойства

2018-07-06

1457

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 1 2 345 Следующая ⇒

Определение.Пусть даны натуральные числа а и b. Говорят, что число а делится на число b, если существует такое натуральное число q, что а = bq.

В этом случае число b называютделителем числа а, а число а - кратным числа b.

Например, 24 делится на 8, так как существует такое q = 3, что 24 = 8×3. Можно сказать иначе: 8 - это делитель числа 24, а 24 есть кратное числа 8.

В том случае, когда а делится на b, пишут: а M b. Эту запись часто читают и так: «а кратно b».

Заметим, что понятие «делитель данного числа» следует отличать от понятия «делитель», обозначающего то число, на которое делят. Например, если 18 делят на 5, то число 5 - делитель, но 5 не является делителем числа 18. Если 18 делят на 6, то в этом случае понятия «делитель» и «делитель данного числа» совпадают.

Из определения отношения делимости и равенства a = 1 × а, справедливого для любого натурального а, вытекает, что 1 является делителем любого натурального числа.

Выясним, сколько вообще делителей может быть у натурального числа а. Сначала рассмотрим следующую теорему.

Теорема 1. Делитель b данного числа а не превышает этого числа, т. е. если а M b, то b £ а.

Доказательство. Так как а M b, то существует такое qÎ N, что а = bq и, значит, а - b = bq - b = b ×(q - 1). Поскольку qÎ N, то q ³ 1. . Тогда b ×(q - 1) ³ 0 и, следовательно, и b £ а.

Из данной теоремы следует, что множество делителей данного числа конечно. Назовем, например, все делители числа 36. Они образуют конечное множество {1,2,3,4,6,9,12,18,36}.

В зависимости от числа делителей среди натуральных чисел различают простые и составные числа.

Определение.Простым числом называется такое натуральное число, большее 1, которое имеет только два делителя - единицу и само это число.

Например, 13 – простое, поскольку у него только два делителя: 1 и 13.

Определение.Составным числом называется такое натуральное число, которое имеет более двух делителей.

Так число 4 составное, у него три делителя: 1, 2 и 4. Число 1 не является ни простым, ни составным числом в связи с тем, что оно имеет только один делитель.

Чисел, кратных данному числу, можно назвать как угодно много, - их бесконечное множество. Так, числа, кратные 4, образуют бесконечный ряд: 4, 8, 12, 16, 20, 24, .... и все они могут быть получены по формуле а=4q, где q принимает значения 1, 2, 3,... .

Нам известно, что отношение делимости на множестве N обладает рядом свойств, в частности, оно рефлексивно, антисимметрично и транзитивно. Теперь, имея определение отношения делимости, мы можем доказать эти и другие его свойства.

Теорема 2. Отношение делимости рефлексивно, т.е. любое натуральное число делится само на себя.

Доказательство. Для любого натурального а справедливо равенство а=а×1. Так как 1 Î N то, по определению отношения делимости, аMа.

Теорема 3. Отношение делимости антисимметрично, т.е. если а M b и а ¹ b, то .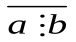

Доказательство. Предположим противное, т. е. что bMа. Но тогда а£b, согласно теореме, рассмотренной выше.

По условию а M b и а ¹ b. Тогда, по той же теореме, b £ а.

Неравенства а £ b и b £ а.будут справедливы лишь тогда, когда а = b, что противоречит условию теоремы. Следовательно, наше предположение неверное и теорема доказана.

Теорема 4. Отношение делимости транзитивно, т.е. если аM b и b M с, то а M с.

Доказательство. Так как а M b, то существует такое натуральное число q, что а = b q , а так как bM с, то существует такое натуральное число р, что b = ср. Но тогда имеем: а = b q = (ср)q = с(рq). Число рq - натуральное. Значит, по определению отношения делимости, а. M с.

Теорема 5 (признак делимости суммы). Если каждое из натуральных чисел а_1,а₂,…а_п делится на натуральное число b, то и их сумма а_{1 +}а_{2 +}… + а_п делится на это число.

Например, не производя вычислений, можно сказать, что сумма 175 + 360 +915 делится на 5, так как на 5 делится каждое слагаемое этой суммы.

Теорема 6 (признак делимости разности). Если числа а₁и а₂делятся на b и а₁³ а₂, то их разность а₁- а₂делится на b.

Теорема 7 (признак делимости произведения). Если число а делится на b, то произведение вида ах, где х е N. делится на b.

Из теоремы следует, что если один из множителей произведения делится на натуральное число b, то и все произведение делится на b.

Например, произведение 24×976×305 делится на 12, так как на 12 делится множитель 24.

Рассмотрим еще три теоремы, связанные с делимостью суммы и произведения, которые часто используются при решении задач на делимость.

Теорема 8. Если в сумме одно слагаемое не делится на число b, а все остальные слагаемые делятся на число b, то вся сумма на число b не делится.

Например, сумма 34 + 125 + 376 + 1024 на 2 не делится, так как 34:2,376^:2,124^:2,но 125 не делится на 2.

Теорема 9. Если в произведении аb множитель а делится на натуральное число т, а множитель b делится на натуральное число п то а b делится на тп.

Справедливость этого утверждения вытекает из теоремы о делимости произведения.

Теорема 10. Если произведение ас делится на произведение bс, причем с - натуральное число, то и а делится на b.

2. Простые и составные числа

Простые числа играют большую роль в математике - по существу они являются «кирпичами», из которых строятся составные числа.

Это утверждается в теореме, называемой основной теоремой арифметики натуральных чисел, которая приводится без доказательства.

Теорема. Любое составное число можно единственным образом представить в виде произведения простых множителей.

Например, запись 110=2×5×11 есть представление числа 110 в виде произведения простых множителей или разложение его на простые множители.

Два разложения числа на простые множители считают одинаковыми, если они отличаются друг от друга лишь порядком множителей. Поэтому представление числа 110 в виде произведения 2×5×11 или произведения 5×2×11 есть, по существу, одно и то же разложение числа 110 на простые множители.

Раскладывая числа на простые множители, используют признаки делимости на 2, 3, 5 и др. Напомним один из способов записи разложения чисел на простые множители. Разложим, например, на множители число 90. Число 90 делится на 2. Значит, 2 есть один из простых множителей в разложении числа 90. Разделим 90 на 2. Число 2 запишем справа от знака равенства, а частное 45 - под числом 90. Число 45 делим на простое число 3, получаем 15. Делим 15 на 3, получаем 5. Число 5 - простое, при делении его на 5 получаем 1. Разложение на множители закончено.

90 =2×3×3×5

45, 15, 5, 1

При разложении числа на простые множители произведение одинаковых множителей представляют в виде степени: 90=2×3²×5; 60=2²× 3× 5; 72=2³×3². Такое разложение числа на простые множители называют каноническим.

Греческий математик - Евклид доказал, что множество простых чисел бесконечно.

Действительно, предположим, что множество простых чисел конечное и исчерпывается числами 2, 3, 5, 7, ...,р, где p - самое большое простое число. Перемножим все простые числа и их произведение обозначим через а. Прибавим к этому числу 1. Каким будет полученное число а + 1 - простым или составным?

Простым число а+1 быть не может, потому что оно больше самого большого простого числа, а по предположению таких простых чисел не существует. Но составным оно тоже быть не может: если а+1 составное, то оно должно иметь хотя бы один простой делитель q. Так как число а = 2×3×5 ×...×р также делится на это простое число q, то и разность (а + 1) - а, т.е. число 1, делится на q, что невозможно.

Итак, число а не является ни простым, ни составным, но этого тоже не может быть - всякое число, отличное от 1, либо простое, либо составное. Следовательно, наше предположение о том, что множество простых чисел конечное и есть самое большое простое число, неверно, и значит, множество простых чисел бесконечное.

3. Признаки делимости

Рассмотренные в свойства отношения делимости позволяют доказать известные признаки делимости чисел, записанных в десятичной системе счисления, на 2, 3, 4, 5, 9.

Признаки делимости позволяют установить по записи числа делится ли оно на другое, не выполняя деления.

Теорема 11 (признак делимости на 2). Для того чтобы число х делилось на 2, необходимо и достаточно, чтобы его десятичная запись оканчивалась одной из цифр 0, 2, 4, 6, 8.

Доказательство. Пусть число х записано в десятичной системе счисления, т.е. х=а_п 10^п+а_п-1×10^п–1+…+а₁×10+а_0,где а_п,а_п-1, …, а₁ принимают значения 0, 1,2, 3, 4, 5, 6, 7, 8, 9, а_п ¹0 и а₀ принимает значения 0,2,4,6,8. Докажем, что тогда х M 2.

Так как 10M2, то 10²M2, 10³M2, ..., 10^пM2 и, значит, а_п×10^п+а_п-1×10^п–1+…+а₁×10M2. По условию а₀ тоже делится на 2, и поэтому число х можно рассматривать как сумму двух слагаемых, каждое из которых делится на 2. Следовательно, согласно признаку делимости суммы, число х делится на 2.

Докажем обратное: если число х делится на 2, то его десятичная запись оканчивается одной из цифр 0, 2, 4, 6, 8.

Запишем равенство х=а_п×10^п+а_п-1×10^п–1+…+а₁×10+а₀в таком виде: а₀=х-(а_п×10^п+а_п-1×10^п–1+…+а₁×10). Но тогда, по теореме о делимости разности, а₀M2, поскольку хM2 и (а_п×10^п+а_п-1×10^п–1+…+а₁×10)M2. Чтобы однозначное число а₀ делилось на 2, оно должно принимать значения 0, 2, 4, 6, 8.

Теорема 12 (признак делимости на 5). Для того чтобы число х делилось на 5, необходимо и достаточно, чтобы его десятичная запись оканчивалась цифрой 0 или 5.

Доказательство этого признака аналогично доказательству признака делимости на 2.

Теорема 13 (признак делимости на 4). Для того чтобы число х делилось на 4, необходимо и достаточно, чтобы на 4 делилось двузначное число, образованное последними двумя цифрами десятичной записи числа х.

Доказательство. Пусть число х записано в десятичной системе счисления, т.е. х=а_п×10^п+а_п-1×10^п–1+…+а₁×10+а₀и две последние цифры в этой записи образуют число, которое делится на 4. Докажем, что тогда хM4.

Так как 100M4, то (а_п×10^п+а _п-1×10^п–1+…+а₂×10²)M4. По условию, а₁×10+а₀ (это и есть запись двузначного числа) также делится на 4. Поэтому число х можно рассматривать как сумму двух слагаемых, каждое из которых делится на 4. Следовательно, согласно признаку делимости суммы, и само число х делится на 4.

Докажем обратное, т.е. если число х делится на 4, то двузначное число, образованное последними цифрами его десятичной записи, тоже делится на 4.

Запишем равенство х=а_п×10^п+а _п-1×10^п–1+…+а₁×10+а₀в таком виде: а₁×10+а₀=х-(а_п×10^п+а_п-1×10^п–1+…+а₂×10²). Так как хM4 и (а_п×10^п+а_п-1×10^п–1+…+а₂×10²), то по теореме о делимости разности (а₁×10+а₀)M4. Но выражение а₁×10+а₀есть запись двузначного числа, образованного последними цифрами записи числа х.

Например, число 157872 делится на 4, так как последние две цифры в его записи образуют число 72, которое делится на 4. Число 987641 не делится на 4, так как последние две цифры в его записи образуют число 41, которое не делится на 4.

Теорема 14 (признак делимости на 9). Для того чтобы число х делилось на 9, необходимо и достаточно, чтобы сумма цифр его десятичной записи делилась на 9.

Доказательство.

Докажем сначала, что числа вида 10^п-1 делятся на 9. Действительно,

10^п-1=(9×10^п-1+10^п–1)-1=(9×10^п-1+9×10^п-2+10^п–2)-1=(9×10^п-1+9×10^п-2+...+10)-1=

=9×10^п-1+9×10^п-2+...+9. Каждое слагаемое полученной суммы делится на 9, значит, и число 10^п-1 делится на 9.

Пусть число х=а_п×10^п+а_п-1×10^п–1+…+а₁×10+а₀и (а_п+а_п-1+…+а₁+а₀)M 9. Докажем, что тогда хM9.

Преобразуем сумму а_п×10^п+а_п-1×10^п–1+…+а₁×10+а₀, прибавив и вычтя из нее выражение а_п+а _п-1 +…+а₁+а₀ и записав результат в таком виде:

х=(а_п×10^п-а_п)+(а_п-1×10^п–1-а_п-1)+...+(а₁×10-а₁)+(а₀-а₀)+(а_п+а_п-1+…+а₁+а₀)= =а_п(10^п-1-1)+а_п-1(10^п-1-1)+...+а₁× (10^п-1-1)+(а_п+а _п-1+…+а₁+а₀).

В последней сумме каждое слагаемое делится на 9:

а_п(10^п-1- 1)M9, так как (10^п-1-1)M9,

а _п-1 (10^п-1-1)M9, так как (10^п-1- 1)M9 и т.д.

(а_п+а _п-1+…+а₁+а₀)M 9 по условию.

Следовательно, хM9.

Докажем обратное, т.е. если хM9, то сумма цифр его десятичной записи делится на 9.

Равенство х=а_п×10^п+а_п-1×10^п–1+…+а₁×10+а₀запишем в таком виде:

а_п+а_п-1+…+а₁+а₀=х-(а_п(10^п-1)+а_п-1(10^п–1-1)+...+а₁(10-1)).

Так как в правой части этого равенства и уменьшаемое, и вычитаемое кратны 9, то по теореме о делимости разности (а_п + а_п-1 + …+ а₁+ а₀)M9, т.е. сумма цифр десятичной записи числа х делится на 9, что и требовалось доказать.

Например, число 34578 делится на 9, так как сумма его цифр, равная 27 делится на 9. Число 130542 не делится 9, так как сумма его цифр, равная 15, не делится на 9.

Теорема 15 (признак делимости на 3). Для того чтобы число х делилось на 3, необходимо и достаточно, чтобы сумма цифр его десятичной записи делилось на 3.

Доказательство этого утверждения аналогично доказательству признака делимости на 9.

Мы рассмотрели признаки делимости чисел на 2, 3, 4, 5, 9. Из школьного курса математики известен еще ряд других, например, на 10 и 25. Конечно, этого недостаточно, чтобы решать вопросы делимости. Существует общий признак делимости для чисел, записанных в любой позиционной системе счисления, открытый в XVII веке французским математиком Паскалем. Мы рассмотрим его для случая, когда основанием системы счисления является число 10.

Теорема 16 (признак делимости Паскаля). Число х = а_п× 10^п + а _п-1 × 10^п ^–1+ …+ а₁× 10 + а₀делится на число b тогда и только тогда, когда на b делится сумма а_п× r_п + а _п-1 × r_{п –1}+ …+ а₁× r₁ + а₀, где r₁, r₂,…,r_n - остатки от деления на bразрядных единиц 10, 10²,..., 10ⁿ_.

Используя этот признак, выведем, например, известный признак делимости на 3 в десятичной системе счисления.

Найдем остатки от деления разрядных единиц на 3:

10 =3×3+1(r₁=1);

10²= 3×33 + 1 (r₂= 1);

10³= 10²•10= (3×33 + 1) × ( 3×3 + 1) =3q₃+ 1 (r₃ = 1).

На основании рассмотренных случаев можно предположить, что ("n Î N) 10ⁿ=3q_n+1. Убедиться в истинности этого утверждения можно, если воспользоваться методом математической индукции.

Таким образом, доказано, что число делится на 3 тогда и только тогда, когда сумма цифр его десятичной записи делится на 3.

Используя признак делимости Паскаля, можно доказать следующий признак делимости чисел на 11: для того чтобы число делилось на 11, необходимо и достаточно, чтобы разность между суммой его цифр, стоящих на нечетных местах, и суммой цифр, стоящих на четных местах, делилась на 11. Обычно при нахождении разности из большего числа вычитают меньшее.

Например, число 540309 делится на 11, так как (4 + 3 + 9) - (5 + 0 + 0) = 11, а 11 : 11. Число 236 не делится на 11, поскольку (2 + 6) - 3 = 5, но 5 не кратно 11.

4. Наименьшее общее кратное и наибольший общий делитель

Рассмотрим известные из школьного курса математики понятия наименьшего общего кратного и наибольшего общего делителя натуральных чисел, сформулируем их основные свойства, опустив все доказательства.

Определение.Общим кратным натуральных чисел а и b называется число, которое кратно каждому из данных чисел.

Наименьшее число из всех общих кратных чисел а и b называется наименьшим общим кратным этих чисел.

Наименьшее общее кратное чисел а и b условимся обозначать К(а, b). Например, два числа 12 и 18 общими кратными являются: 36, 72, 108, 144, 180 и т.д. Число 36 - наименьшее общее кратное чисел 12 и 18. Можно записать: К(12,18) = 36.

Для наименьшего общего кратного справедливы следующие утверждения:

1. Наименьшее общее кратное чисел а и b всегда существует и является единственным.

2. Наименьшее общее кратное чисел а и b не меньше большего из данных чисел, т.е. если а > b, то К(а, b) ³ а.

3. Любое общее кратное чисел а и b делится на их наименьшее общее кратное.

Определение.Общим делителем натуральных чисел а и b называется число, которое является делителем каждого из данных чисел.

Наибольшее число из всех общих делителей чисел а и b называется наибольшим общим делителем данных чисел. Наибольший общий делитель чисел а и b условимся обозначать D(а, b).

Например, для чисел 12 и 18 общими делителями являются числа: 1,2,3,6. Число 6 - наибольший общий делитель чисел 12 и 18. Можно записать: D(12,8)=6.

Число 1 является общим делителем любых двух натуральных чисел а и b. Если у этих чисел нет иных общих делителей, то D(а, b) = 1, а числа а и b называются взаимно простыми.

Например, числа 14 и 15 - взаимно простые, так как D (14, 15) = 1.

Для наибольшего общего делителя справедливы следующие утверждения:

1. Наибольший общий делитель чисел а и b всегда существует и является единственным.

2. Наибольший общий делитель чисел а и b не превосходит меньшего из данных чисел, т.е. если а < b, то D (а, b) £ а.

3. Наибольший общий делитель чисел а и b делится на любой общий делитель этих чисел.

Наименьшее общее кратное чисел а и b и их наибольший общий делитель взаимосвязаны: произведение наименьшего общего кратного и наибольшего общего делителя чисел а и b равно произведению этих чисел, т.е.

К(а, b)×D(а,b)=а×b.

Из этого утверждения вытекают следующие следствия:

а) Наименьшее общее кратное двух взаимно простых чисел равно произведению этих чисел, т. е. D(а,b) = 1 ÞК(а,b)=а× b.

Например, чтобы найти наименьшее общее кратное чисел 14 и 15, достаточно их перемножить, так как D (14, 15) = 1.

б) Для того чтобы натуральное число а делилось на произведение взаимно простых чисел m и n, необходимо и достаточно, чтобы оно делилось и на m, и на n.

Это утверждение представляет собой признак делимости на числа, которые можно представить в виде произведения двух взаимно простых чисел.

Например, так как 6=2× 3 и D(2,3)=1, то получаем признак делимости на 6: для того чтобы натуральное число делилось на 6, необходимо и достаточно, чтобы оно делилось на 2 и на 3.

Заметим, что данный признак можно применять многократно. Сформулируем, например, признак делимости на 60: для того чтобы число делилось на 60, необходимо и достаточно, чтобы оно делилось и на 4, и на 15. В свою очередь, число будет делиться на 15 тогда и только тогда, когда оно делится и на 3, и на 5. Обобщая, получаем следующий признак делимости на 60: для того чтобы число делилось на 60, необходимо и достаточно, чтобы оно делилось на 4, на 3 и на 5.

2018-07-06

1457

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 1 2 345 Следующая ⇒

Обсуждение в статье: Отношение делимости и его свойства

Обсуждений еще не было, будьте первым... ↓↓↓