Постоянное раздельное резервирование

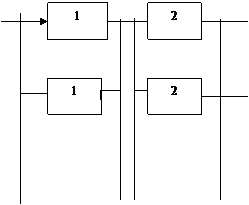
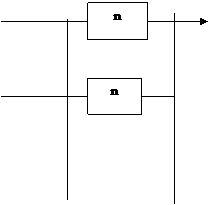
Изобразим схему замещения при постоянном раздельном резервировании (рис. 3.8).

Рисунок 3.8

Вероятность того, что произойдет отказ элементов i -го типа, равна произведению вероятностей отказов i-го элемента и всех элементов, его резервирующих, т. е.

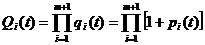(3.12)

Вероятность безотказной работы i-го и всех резервирующих его эле-
ментов

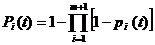(3.13)

Если резервные и резервируемые элементы равнонадежны, то

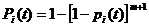(3.14)

Поскольку функциональные группы элементов соединены последова­тельно, то вероятность безотказной работы в целом равна произведению ве- роятностей безотказной работы функциональных групп, т. е.

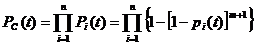(3.15)

Если все элементы равнонадежны, то

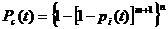(3.16)

4.2. Расчет надежности при резервировании систем с дробной кратностью.

При резервировании с дробной кратностью нормальная работа резервированного соединения возможна при условии, если число исправных элементов не меньше необходимого для нормальной работы.

Кратность резервирования определяется из соотношения

Где Z – общее число элементов расчета резервированного соединения;

N- число элементов, необходимое для нормальной работы соединения;

Z – N=М - число резервных элементов.

На рисунке 3.9 представлена система резервирования с дробной кратностью, состоящая из N основных и M резервных элементов.

В случае общего резервирования кратность резервирования всегда равна числу резервных устройств.

Кратность резервирования всегда записывают в виде простой дроби без сокращения.

Например, если записано K = 2/4 , то это означает, что здесь имеет место резервирование с дробной кратностью, причем для нормальной работы соединения необходимо не менее двух элементов, при этом число резервных элементов равно четырем.

Пусть резервированная система состоит из N основных и М резервных элементов (N>M). При отказе одного из основных элементов на его место без перерыва в работе включается один из резервных.

Средняя наработка до отказа такой резервированной системы при равнонадежных элементах равна:

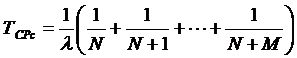
Безотказная работа системы в течении времени t будет иметь место, если за это время осуществится хотя бы одна гипотеза: Н0 – все элементы исправны; H1– один элемент отказал, (М + N -1) элементов исправны; (Hi – i) элементов отказали; ( М + N – i) элементов исправны; (Hk – М) элементов отказали, N элементов исправны.

Число различных состояний системы можно описать выражением:

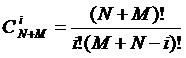(3.18)

Вероятность безотказной работы системы с резервированием с дробной кратностью может быть определена выражением

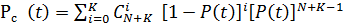(3.19)