Модель МакКаллока - Питса

Нейрон является единицей обработки информации в нейронной сети. Из приведенных выше рассуждений следует, что каждый нейрон суммирует с соответствующими весами сигналы, приходящие от других нейронов, выполняет нелинейную решающую функцию и передает результат связанным с ним другим нейронам. В простейших моделях нейронов выходной сигнал принимает двоичные значения: 0 или 1. Значение 1 соответствует превышению порогового уровня, значение 0 – в противном случае. Одна из первых моделей нейрона была предложена Дж. МакКаллоком и У. Питсом в 1943 году [4]. Структурная схема этой модели представлена на рис. 1.3.

Сигналы x_j на входе синапсов j (j = 1,2,…,N), связанные с нейроном i, суммируются с учетом соответствующих синаптических весов w_ij (первый индекс относится к нейрону, а второй к синапсу), после чего результат сравнивается с пороговым значением w_i0 .

Пороговое значение отражает увеличение или уменьшение входного сигнала, подаваемого на функцию активации, которая ограничивает амплитуду выходного сигнала. Выходной сигнал нейрона y_i определяется при этом зависимостью

(1.1)

+

1

x1

x2

wj1

wj2

wj0

xN

wjN

uj

yj

 

 

 

Рис. 1.3 Модель нейрона МакКаллока-Питса

Аргументом функции выступает суммарный сигнал, формируемый сумматором искусственного нейрона.

. (1.2)

Коэффициенты 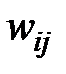в формуле (1.1) представляют веса синапсов. Положительные значения соответствует синапсам, повышающим потенциал, отрицательные значения – синапсам, понижающим потенциал, свидетельствует об отсутствии связи между i-м и j-м нейронами.

Использование порогового сигнала обеспечивает эффект аффинного преобразования выхода линейного сумматора .

Модель МакКаллока – Питса – это дискретная модель, в которой состояние нейрона в момент (t+1) рассчитывается по значению его входных сигналов в момент времени t.

Функция f(u_i) называется функцией активации. В модели МакКаллока – Питса это пороговая функция вида:

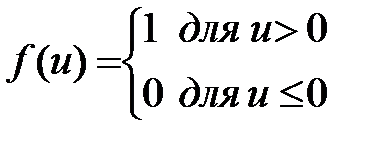. (1.3)

В общем случае эта функция активации описывается следующим выражением:

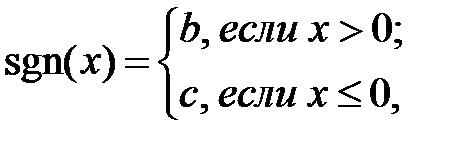(1.4)

где b и c – некоторые постоянные. На практике чаще всего используют две пары постоянных b и c: первая (-1,1); вторая – (0,1). Первая пара коэффициентов определяет так называемую симметричную пороговую функцию, вторая – смещенную.

Персептрон

Ф. Розенблатт в 1958 году ввел понятие персептрона как первой модели обучения с учителем [4].Обучение персептрона требует наличие учителя и состоит в таком подборе весов ,чтобывыходной сигнал был наиболее близок к заданному значению . При таком способе обучения, каждой обучающей выборке, представленной вектором x поставлено в соответствии ожидаемое значение 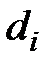на выходе i-го нейрона.

Наиболее популярный метод обучения персептрона, называемый правилом персептрона, состоит в подборе весовых коэффициентов по следующему алгоритму:

· при первоначально выбранных (как правило, случайным образом) значениях весов на вход нейрона подается обучающий вектор x и рассчитывается значение выходного сигнала 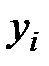. По результатам сравнения значения 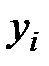с заданным значением 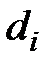уточняются значения весов;

· если 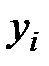совпадает с ожидаемым значением 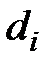, то весовые коэффициенты w_ijне изменяются;

· если 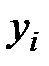=0 , а соответствующее значение 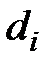=1 , то значения весов уточняются по формуле , где (t+1)– это номер текущего цикла, а t – номер предыдущего цикла;

· если 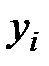=1 , а соответствующее значение 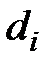=0 , то значения весов уточняются по формуле 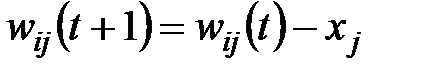, где (t+1)– это номер текущего цикла, а t – номер предыдущего цикла;

По завершении уточнения весов предоставляются очередной обучающий вектор x и связанное с ним значение 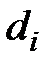, и значения весов уточняются заново. Этот процесс повторяется для всех обучающих выборок, пока не будут минимизированы различия между всеми значениями 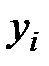и соответствующими им значениями .

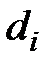Сигмоидальный нейрон

Нейрон сигмоидального типа имеет структуру, подобную модели МакКаллока–Питса, с той разницей, что функция активации является непрерывной и может быть выражена в виде сигмоидальной униполярной или биполярной функции [4].Структура нейрона представлена на рис. 1.4.

Входные сигналы (j=1,2,…,N) суммируются с учетом соответствующих весов (сигнал поступает в направлении от узла j к узлу i) в сумматоре, после чего результат сравнивается с пороговым значением 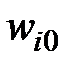. Выходной сигнал нейрона y_i определяется при этом зависимостью

. (1.9)

Аргументом функции выступает суммарный сигнал . Функция f(u_i), называемая функцией активации, относится к классу непрерывных, монотонно возрастающих и дифференцируемых функций. Нейрон сигмоидального типа использует сигмоидальную униполярную (логистическую) или сигмоидальную биполярную (гиперболический тангенс) функцию активации.

+

1

wj0

x1

wi1

x2

wi2

xN

wiN

ui

yi

Рис. 1.4 Модель сигмоидального нейрона

Униполярная функция, как правило, представляется формулой

, (1.10)

тогда как биполярная функция задается в виде (1.11) или (1.12):

. (1.11)

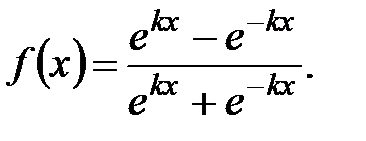(1.12)

Графики сигмоидальных функций при k=1 представлены на рис. 1.5.

Отметим, что, как правило, современные компьютеры вычисляют функцию гиперболического тангенса быстрее, чем логистическую. Другое преимущество функции гиперболического тангенса состоит в том, что она изменяется в диапазоне от –1 до +1. Часто бывает необходимо нормировать обучающий набор данных таким образом, чтобы среднее значение было равно 0 при единичном стандартном отклонении.

Такая нормировка возможна только с функцией активации, которая способна принимать отрицательные значения. И наконец, нечетная функция, такая, как гиперболический тангенс, обеспечивает более быстрое обучение, чем несимметричная логистическая функция.

В этих формулах параметр k подбирается пользователем. Его значение влияет на форму функции активации. При малых значениях k график функции достаточно пологий, по мере роста значения kкрутизна графика увеличивается.

f(x)

x

0.5

а)

f(x)

x

-1

б)

 

Рис. 1.5 Графики сигмоидальных функций:
а – логистическая; б – гиперболический тангенс

При k → ∞ сигмоидальная функция превращается в пороговую функцию, идентичную функции активации персептрона. На практике чаще всего для упрощения используется значение k =1.

Важным свойством сигмоидальной функции является ее дифференцируемость. Для униполярной функции имеем

, (1.13)

тогда как для биполярной функции

. (1.14)

И в первом, и во втором случае график изменения производной относительно переменной x имеет колоколообразную форму, а его максимум соответствует значению x=0.

Сигмоидальный нейрон, как правило, обучается с учителем.

При обучении с учителем предполагается, что помимо входных сигналов, составляющих вектор x, известны также и ожидаемые выходные сигналы нейрона , составляющие вектор d. В подобной ситуации подбор весовых коэффициентов должен быть организован так, чтобы фактические выходные сигналы нейрона принимали бы значения, как можно более близкие к ожидаемым значениям 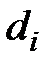. Ключевым элементом процесса обучения с учителем является знание ожидаемых значений 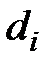выходного сигнала нейрона.

При обучении с учителем производится минимизация целевой функции, которая для единичного обучающего кортежа <x, d>i-го нейрона определяется в виде

(1.15)

где

. (1.16)

Применение непрерывной функции активации позволяет использовать при обучении градиентные алгоритмы.

Нейрон типа WTA

В соответствии с принципами функционирования биологических нейронов созданы различные математические модели, которыми в большей или меньшей степени реализуются свойства природной нервной клетки. Обобщенная схема, составляющая основу большинства таких моделей, восходит к представленной на рисунке 1.3 модели МакКаллока-Питса, содержащий сумматор взвешенных входных сигналов и нелинейный блок выработки выходного сигнала нейрона, функционально зависящего от выходного сигнала сумматора. Однако, существуют и другие модели нейронов существенно отличающиеся от модели МакКаллока–Питса.

Рассмотрим более подробно нейроны типа WTA(winnertakesall – победитель получает все) [4].Эти нейроны имеют входной модуль в виде стандартного сумматора, рассчитывающего сумму входных сигналов с соответствующими весами . Выходной сигнал i-го сумматора определяется согласно формуле:

(1.17)

Группа конкурирующих между собой нейронов получает одни и те же входные сигналы . Выходные сигналы нейронов сравниваются между собой, и по результатам сравнения победителем признается нейрон, значение выходного сигнала у которого оказалось наибольшим. Нейрон-победитель вырабатывает на своем выходе состояние 1, а остальные нейроны переходят в состояние 0. Для обучения нейронов типа WTA не требуется учитель. На начальном этапе случайным образом выбираются весовые коэффициенты каждого нейрона, нормализуемые относительно 1. После подачи первого входного вектора xопределяется победитель этапа. Победивший нейрон переходит в состояние 1, что позволяет провести уточнение весов его входных линий по следующему правилу:

(1.18)

Проигравшие нейроны не изменяют свои весовые коэффициенты.

Схема соединения нейронов типа WTA изображена на рис.1.6.

На функционирование нейронов типа WTA оказывает существенное влияние нормализация входных векторов и весовых коэффициентов. Выходной сигнал i-го нейрона может быть описан векторным отношением:

(1.19)

Поскольку , значение выходного сигнала определяется углом между векторами x и w. Поэтому победителем оказывается нейрон, вектор весов которого оказывается наиболее близким текущему обучаемому вектору.

 

Механизм конкуренции нейронов

+

+

+

x1

x2

xN

u1

u2

uK

w11

w12

w1N

wK1

wK2

wKN

y1

yK

y2

 

Рис. 1.6 Схема соединения нейронов типа WTA

В результате победы нейрона уточняются его весовые коэффициенты, значения которых приближаются к значениям вектора x. Проигравшие нейроны не изменяют свои веса. Следствием такой конкуренции становится самоорганизация процесса обучения.