Алгоритм наискорейшего спуска

Если при разложении целевой функции E(w) в ряд Тейлора ограничиться ее линейным приближением, то мы получим алгоритм наискорейшего спуска. Для выполнения соотношения 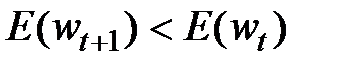достаточно подобрать 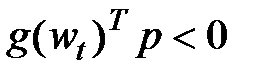. Условию уменьшения значения целевой функции отвечает выбор вектора направления

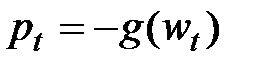. (2.21)

В этом случае коррекция весовых коэффициентов производится по формуле:

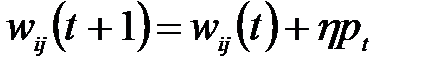(2.22)

В другом виде формулу коррекции весов по методу наискорейшего спуска можно представить следующим образом:

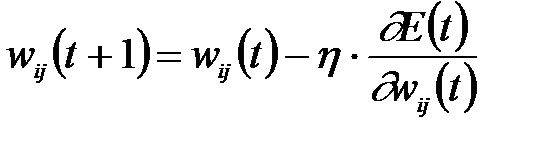(2.23)

Ограничение слагаемым первого порядка при разложении функции в ряд Тейлора, не позволяет использовать информацию о ее кривизне. Это обуславливает линейную сходимость метода. Указанный недостаток, а также резкое замедление минимизации в ближайшей окрестности точки оптимального решения, когда градиент принимает очень малые значения, делают алгоритм наискорейшего спуска низкоэффективным. Тем не менее, простота, невысокие требования к объему памяти и относительно невысокая вычислительная сложность, обуславливают широкое использование алгоритма. Повысить эффективность удается путем эвристической модификации выражения, определяющего направление градиента.

Одна из модификаций получила название алгоритма обучения с моментом. При этом подходе уточнение весов сети производится по формуле:

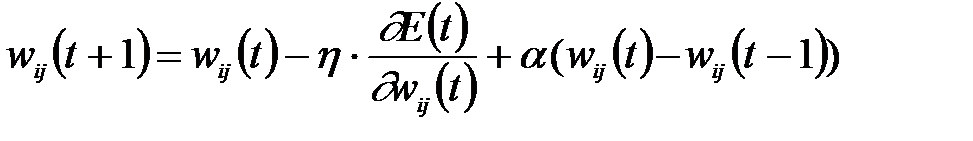(2.24)

где a - это коэффициент момента, принимающий значения в интервале [0, 1].

Первое слагаемое в формуле (2.24) соответствует алгоритму наискорейшего спуска, а второе слагаемое учитывает последнее изменение весов и не зависит от фактического значения градиента. Чем больше значение коэффициента a, тем большее значение оказывает показатель момента на подбор весов. При постоянном значении коэффициента обучения 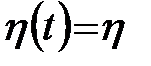приращение весов остается примерно одинаковым, то есть 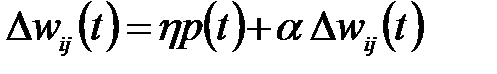, поэтому эффективное приращение весов можно писать формулой:

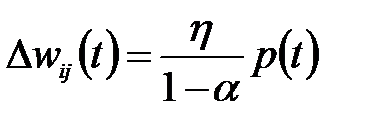(2.25)

При значении a=0,9 это соответствует десятикратному увеличению значения коэффициента обучения и, следовательно, десятикратному ускорению процесса обучения. При малых значениях градиента показатель момента начинает доминировать, что приводит к такому приращению весов, которое соответствует увеличению значения целевой функции, позволяющему выйти из зоны локального минимума. Однако показатель момента, не должен доминировать на протяжении всего процесса обучения, поскольку это приводит к нестабильности алгоритма. На практике, увеличение целевой функции не допускается больше, чем на 4%. В противном случае, 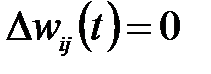. При этом показатель градиента начинает доминировать над показателем момента и процесс развивается в направлении минимизации, заданном вектором градиента [2].